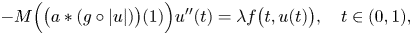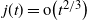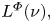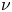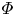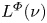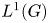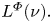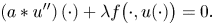Refine search
Actions for selected content:
84 results
5 - Key-recovery techniques
-
- Book:
- Linear Cryptanalysis
- Published online:
- 17 December 2025
- Print publication:
- 20 November 2025, pp 64-73
-
- Chapter
- Export citation
6 - Statistical Learning
- from Part III - Advanced Concepts
-
- Book:
- Statistics for Chemical Engineers
- Published online:
- 12 December 2025
- Print publication:
- 25 September 2025, pp 289-384
-
- Chapter
- Export citation
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

The Art of Inpainting
- Mathematical Methods for the Virtual Restoration of Illuminated Manuscripts
-
- Published online:
- 22 May 2025
- Print publication:
- 22 May 2025
4 - Deep Learning Inpainting Methods
-
- Book:
- The Art of Inpainting
- Published online:
- 22 May 2025
- Print publication:
- 22 May 2025, pp 115-161
-
- Chapter
- Export citation
An axiomatics and a combinatorial model of creation/annihilation operators
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 10 April 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimating an Unobserved Component of a Serial Response Time Model
-
- Journal:
- Psychometrika / Volume 44 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 01 January 2025, pp. 473-484
-
- Article
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
2 - Review of Mathematics
-
- Book:
- Applied Hydrology
- Published online:
- 09 July 2024
- Print publication:
- 04 July 2024, pp 11-35
-
- Chapter
- Export citation
3 - Linear Time-Invariant Systems
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 62-116
-
- Chapter
- Export citation
1 - Background
- from Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 3-49
-
- Chapter
- Export citation
8 - Deep Learning
-
- Book:
- Introduction to Intelligent Systems, Control, and Machine Learning using MATLAB
- Published online:
- 27 November 2023
- Print publication:
- 16 November 2023, pp 252-322
-
- Chapter
- Export citation
2 - Linear Invariant Systems and Fourier Analysis
-
- Book:
- Modern Information Optics with MATLAB
- Published online:
- 22 December 2022
- Print publication:
- 05 January 2023, pp 21-69
-
- Chapter
- Export citation
AFFINE CONVOLUTIONS, RAMANUJAN–FOURIER EXPANSIONS AND SOPHIE GERMAIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 11-18
- Print publication:
- August 2023
-
- Article
- Export citation
20 - Convolution, Filtering with the Window Method
-
- Book:
- Time Series Data Analysis in Oceanography
- Published online:
- 21 April 2022
- Print publication:
- 05 May 2022, pp 357-373
-
- Chapter
- Export citation
Convolution and deconvolutional treatment on sample transparency aberration in Bragg–Brentano geometry
-
- Journal:
- Powder Diffraction / Volume 37 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 02 May 2022, pp. 13-21
-
- Article
- Export citation
Renewal theory for iterated perturbed random walks on a general branching process tree: intermediate generations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 421-446
- Print publication:
- June 2022
-
- Article
- Export citation
5 - Set Functions and Measures
-
- Book:
- Counterexamples in Measure and Integration
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 100-122
-
- Chapter
- Export citation
Convolution structures for an Orlicz space with respect to vector measures on a compact group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 87-98
-
- Article
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation