Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-25T21:38:35.876Z Has data issue: false hasContentIssue false
  • English
  • Français

AFFINE CONVOLUTIONS, RAMANUJAN–FOURIER EXPANSIONS AND SOPHIE GERMAIN PRIMES

Part of: Multiplicative number theory Elementary number theory

Published online by Cambridge University Press:  25 October 2022

ELIEZER FUENTES Open the ORCID record for ELIEZER FUENTES [Opens in a new window]
ELIEZER FUENTES*
Affiliation:
Mathematics Department, Pontificia Universidad Católica de Chile, Santiago, Chile
*
e-mail: eifuentesq@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For a fixed integer h, the standard orthogonality relations for Ramanujan sums 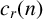$c_r(n)$ give an asymptotic formula for the shifted convolution 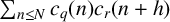$\sum _{n\le N} c_q(n)c_r(n+h)$. We prove a generalised formula for affine convolutions 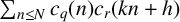$\sum _{n\le N} c_q(n)c_r(kn+h)$. This allows us to study affine convolutions 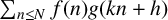$\sum _{n\le N} f(n)g(kn+h)$ of arithmetical functions 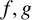$f,g$ admitting a suitable Ramanujan–Fourier expansion. As an application, we give a heuristic justification of the Hardy–Littlewood conjectural asymptotic formula for counting Sophie Germain primes.

Keywords

Ramanujan–Fourier expansionconvolutionSophie Germain primes

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11N05: Distribution of primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 11 - 18
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carmichael, R. D., ‘Expansions of arithmetical functions in infinite series’, Proc. Lond. Math. Soc. (2) 34 (1932), 1–26.CrossRefGoogle Scholar
Coppola, G. and Murty, M. R., ‘Finite Ramanujan expansions and shifted convolution sums of arithmetical functions, II’, J. Number Theory 185 (2018), 16–47.CrossRefGoogle Scholar
Coppola, G., Murty, M. R. and Saha, B., ‘On the error term in a Parseval type formula in the theory of Ramanujan expansions II’, J. Number Theory 160 (2016), 700–715.CrossRefGoogle Scholar
Coppola, G., Murty, M. R. and Saha, B., ‘Finite Ramanujan expansions and shifted convolution sums of arithmetical functions’, J. Number Theory 174 (2017), 78–92.CrossRefGoogle Scholar
Gadiyar, H. G., Murty, M. R. and Padma, R., ‘Ramanujan–Fourier series and a theorem of Ingham’, Indian J. Pure Appl. Math. 45(5) (2014), 691–706.CrossRefGoogle Scholar
Gadiyar, H. G. and Padma, R., ‘Ramanujan–Fourier series, the Wiener–Khintchine formula and the distribution of prime pairs’, Phys. A 269(2–4) (1999), 503–510.CrossRefGoogle Scholar
Hardy, G. H., ‘Note on Ramanujan’s trigonometrical function ${c}_q(n)$ and certain series of arithmetical functions’, Math. Proc. Cambridge Philos. Soc. 20 (1921), 263–271.Google Scholar
Ingham, A. E., ‘Some asymptotic formulae in the theory of numbers’, J. Lond. Math. Soc. (2) 2 (1927), 202–208.CrossRefGoogle Scholar
Murty, M. R., ‘Ramanujan series for arithmetical functions’, Hardy–Ramanujan J. 36 (2013), 21–33.Google Scholar
Murty, M. R. and Saha, B., ‘On the error term in a Parseval type formula in the theory of Ramanujan expansions’, J. Number Theory 156 (2015), 125–134.CrossRefGoogle Scholar
Ramanujan, S., ‘On certain trigonometric sums and their applications in the theory of numbers’, Trans. Cambridge Philos. Soc. 22 (1918), 179–199.Google Scholar
Saha, B., ‘A note on arithmetical functions with absolutely convergent Ramanujan expansions’, Int. J. Number Theory 12(6) (2016), 1595–1611.CrossRefGoogle Scholar