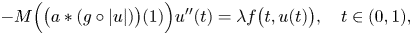Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gu, Qianqian
and
Hao, Zhaocai
2025.
The First Application of the Monotone Iterative Technique in Nonlocal Differential Equations With Convolution Coefficients.
Mathematical Methods in the Applied Sciences,
Vol. 48,
Issue. 13,
p.
13243.