Refine search
Actions for selected content:
59 results
The Repayment Structure of Agricultural Loans under a Full Repayment Constraint
-
- Journal:
- Journal of Agricultural and Applied Economics , FirstView
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal asset allocation and reinsurance problem under enhanced dynamic contagion processes
-
- Journal:
- Annals of Actuarial Science , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of government intervention in balancing economic growth and environmental sustainability: a global dynamics approach across economies
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 22 September 2025, e144
-
- Article
- Export citation
Environmental quality and dishonest behavior: the role of enforcement under propensity for greenery
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 22 September 2025, e145
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal proportional insurance under claim habit
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA , First View
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stationary probabilities and the monotone likelihood ratio in bonus-malus systems
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal monetary policy with a risk-averse central bank
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 12 August 2025, e130
-
- Article
- Export citation
Benchmarking Analysis of Cattle Auction Prices
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 57 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 393-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimizing microplastic pollution in a terrestrial environment: a case for soil-biodegradable mulches
-
- Journal:
- Agricultural and Resource Economics Review / Volume 54 / Issue 2 / August 2025
- Published online by Cambridge University Press:
- 14 May 2025, pp. 495-523
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting risky money
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e88
-
- Article
- Export citation
Economic Opportunities of Bioelectricity from Cotton Gin Waste
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 57 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 14-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A building block approach to retirement income design
-
- Journal:
- Journal of Pension Economics & Finance / Volume 23 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 528-548
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal Beef Cow Culling Strategies in the U.S.: A Dynamic Linear Programing Framework
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 56 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 463-479
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prices, wages and living standards in Spain in the modern era
-
- Journal:
- Revista de Historia Economica - Journal of Iberian and Latin American Economic History / Volume 42 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 14 October 2024, pp. 243-268
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal reinsurance design under distortion risk measures and reinsurer’s default risk with partial recovery
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 October 2024, pp. 738-766
- Print publication:
- September 2024
-
- Article
- Export citation
Benchmark-driven investment for DC pension plans
-
- Journal:
- Journal of Pension Economics & Finance / Volume 23 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 476-503
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal insurance with counterparty and additive background risk
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 02 February 2024, pp. 441-462
- Print publication:
- May 2024
-
- Article
- Export citation
Economic Performance of Rainfed Wheat-Double Crop Systems under Weed Competition
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 56 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 46-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Taxation and policyholder behavior: the case of guaranteed minimum accumulation benefits
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 54 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 185-212
- Print publication:
- January 2024
-
- Article
- Export citation
Reinsurance games with
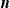 $\boldsymbol{{n}}$ variance-premium reinsurers: from tree to chain
$\boldsymbol{{n}}$ variance-premium reinsurers: from tree to chain
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 706-728
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation