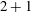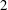Refine search
Actions for selected content:
43 results
Blow-up of cylindrically symmetric solutions for fractional NLS
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On K-stability of blow-ups of weighted projective planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-17
-
- Article
- Export citation
Global existence and some qualitative properties of weak solutions for a class of pseudo-parabolic equations with a logarithmic nonlinearity in whole
 $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-44
-
- Article
- Export citation
Local well-posedness and blow-up in the energy space for the 2D NLS with point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-20
-
- Article
- Export citation
Analysis of a model describing bacterial colony expansion in radial geometry driven by chemotaxis
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 910-947
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence for the fractional p-Laplacian and its application to the extended Nirenberg problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 660-672
- Print publication:
- April 2024
-
- Article
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
ON SYSTEMS OF PARTIAL DIFFERENTIAL EQUATIONS OF BRIOT–BOUQUET TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 122-133
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Lifespan of solutions to wave equations in de Sitter spacetime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 1313-1330
- Print publication:
- December 2018
-
- Article
- Export citation
Evolution of non-simple closed curves in the area-preserving curvature flow
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 659-668
- Print publication:
- June 2018
-
- Article
- Export citation
Convergence Analysis for a Three-Level Finite Difference Scheme of a Second Order Nonlinear ODE Blow-Up Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 679-696
- Print publication:
- November 2017
-
- Article
- Export citation
A FUJITA-TYPE RESULT FOR A SEMILINEAR EQUATION IN HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 420-429
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Global and non Global Solutions for Some Fractional Heat Equations With Pure Power Nonlinearity
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 854-872
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
On mass concentration for the critical generalized Korteweg–de Vries equation
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 519-532
-
- Article
- Export citation
STEFAN PROBLEMS FOR MELTING NANOSCALED PARTICLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 173-176
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Blow-up for the wave equation with nonlinear source and boundary damping terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 20 July 2015, pp. 759-778
- Print publication:
- August 2015
-
- Article
- Export citation
GLOBAL WELL-POSEDNESS AND INSTABILITY OF A NONLINEAR SCHRÖDINGER EQUATION WITH HARMONIC POTENTIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 78-103
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
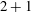 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
A Sylvester-Based IMEX Method via Differentiation Matrices for Solving Nonlinear Parabolic Equations
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1001-1026
- Print publication:
- October 2013
-
- Article
- Export citation
Sharp Threshold of the Gross-Pitaevskii Equation with Trapped Dipolar Quantum Gases
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-387
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation







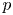
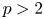

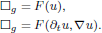
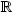 ) concentrate at least the mass of the ground state at the blow-up time. The
) concentrate at least the mass of the ground state at the blow-up time. The