Refine search
Actions for selected content:
23 results
Sobolev regularity of the inverse for minimizers of the neo-Hookean energy satisfying condition INV
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-21
-
- Article
- Export citation
OPTIMAL CONTROL PROBLEMS GOVERNED BY MARGUERRE–VON KÁRMÁN EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 01 January 2025, e38
-
- Article
- Export citation
Stability of isometric immersions of hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the lack of compactness in the axisymmetric neo-Hookean model
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cavitation of a spherical body under mechanical and self-gravitational forces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1143-1173
- Print publication:
- August 2025
-
- Article
- Export citation
Minimal energy for geometrically nonlinear elastic inclusions in two dimensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 769-792
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pressure live loads and the variational derivation of linear elasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1929-1964
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonrigidity of flat ribbons
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 1297-1314
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Γ-convergence and stochastic homogenization of degenerate integral functionals in weighted Sobolev spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 491-544
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rank-one convex, nonpolyconvex isotropic function on
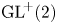 $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
$\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 February 2022, pp. 356-381
- Print publication:
- April 2022
-
- Article
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
Convergence of equilibria for bending-torsion models of rods with inhomogeneities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 233-260
- Print publication:
- February 2020
-
- Article
- Export citation
Surface energies emerging in a microscopic, two-dimensional two-well problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1041-1089
- Print publication:
- October 2017
-
- Article
- Export citation
MULTISYMPLECTIC VARIATIONAL INTEGRATORS FOR NONSMOOTH LAGRANGIAN CONTINUUM MECHANICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e19
-
- Article
-
- You have access
- Open access
- Export citation
Stress constraints in simple bodies undergoing large strains: a variational approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1183-1214
- Print publication:
- December 2015
-
- Article
- Export citation
On a class of nonlinear anisotropic parabolic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1-21
- Print publication:
- February 2016
-
- Article
- Export citation
Attainment results for nematic elastomers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 669-701
- Print publication:
- August 2015
-
- Article
- Export citation
Numerical Method of Fabric Dynamics Using Front Tracking and Spring Model
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 5 / November 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1228-1251
- Print publication:
- November 2013
-
- Article
- Export citation
Numerical analysis of a piezoelectric bone remodelling problem
-
- Journal:
- European Journal of Applied Mathematics / Volume 23 / Issue 5 / October 2012
- Published online by Cambridge University Press:
- 25 May 2012, pp. 635-657
-
- Article
- Export citation
Antiplane Wave Scattering from a Cylindrical Void in a Pre-Stressed Incompressible Neo-Hookean Material
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 2 / February 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 367-382
- Print publication:
- February 2012
-
- Article
- Export citation

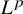
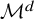
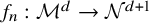
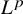
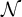
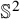

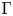
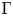
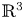
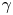
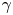
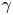
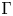
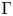
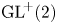
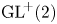
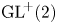
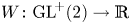
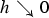
 , for a rod
, for a rod 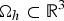
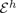 , provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.
, provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.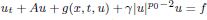
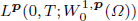 , where the data
, where the data 