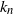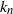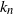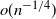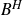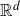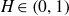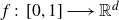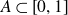Refine search
Actions for selected content:
124 results
Bounds on some geometric functionals of high dimensional Brownian convex hulls and their inverse processes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviors of subcritical branching killed Brownian motion with drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1484-1509
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact solution to the Chow–Robbins game for almost all n, by using a catalan triangle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1206-1241
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discounted optimal stopping zero-sum games in diffusion type models with maxima and minima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 241-270
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Brownian range and the Brownian reversal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 775-794
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal drift rate control and two-sided impulse control for a Brownian system with the long-run average criterion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 271-304
- Print publication:
- March 2025
-
- Article
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 349-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inference on the intraday spot volatility from high-frequency order prices with irregular microstructure noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 858-885
- Print publication:
- September 2024
-
- Article
- Export citation
De Finetti’s control problem with a concave bound on the control rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 January 2024, pp. 834-850
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on Bourgain’s constant for harmonic measure
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1967-1986
- Print publication:
- December 2024
-
- Article
- Export citation
ON THE EXPECTED UNIFORM ERROR OF BROWNIAN MOTION APPROXIMATED BY THE LÉVY–CIESIELSKI CONSTRUCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 581-593
- Print publication:
- June 2024
-
- Article
- Export citation
An elementary approach to the inverse first-passage-time problem for soft-killed Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 279-300
- Print publication:
- March 2024
-
- Article
- Export citation
Optimal coupling of jumpy Brownian motion on the circle
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 18-32
- Print publication:
- March 2024
-
- Article
- Export citation
OPTIMAL STOPPING PROBLEMS WITH A RANDOM TIME HORIZON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 345-346
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Workload analysis of a two-queue fluid polling model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 March 2023, pp. 1003-1030
- Print publication:
- September 2023
-
- Article
- Export citation
An ergodic theorem for asymptotically periodic time-inhomogeneous Markov processes, with application to quasi-stationarity with moving boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 672-700
- Print publication:
- June 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discounted optimal stopping problems in first-passage time models with random thresholds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 June 2022, pp. 714-733
- Print publication:
- September 2022
-
- Article
- Export citation
Probability of total domination for transient reflecting processes in a quadrant
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1094-1138
- Print publication:
- December 2022
-
- Article
- Export citation
Images of fractional Brownian motion with deterministic drift: Positive Lebesgue measure and non-empty interior
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 693-713
- Print publication:
- November 2022
-
- Article
- Export citation