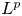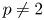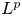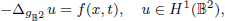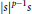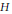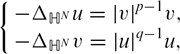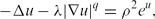Refine search
Actions for selected content:
11 results
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence results for semilinear problems in the two-dimensional hyperbolic space involving critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 141-176
- Print publication:
- February 2017
-
- Article
- Export citation
Infinitely Many Rotationally Symmetric Solutions to a Class of Semilinear Laplace–Beltrami Equations on Spheres
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-729
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Existence Theorems for a Class of Edge-Degenerate Elliptic Equations on Singular Manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 17 February 2015, pp. 355-377
-
- Article
-
- You have access
- Export citation
The Weyl Problem With Nonnegative Gauss Curvature In Hyperbolic Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-131
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
SYMMETRY AND EXISTENCE OF SOLUTIONS OF SEMI-LINEAR ELLIPTIC SYSTEMS IN HYPERBOLIC SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 519-541
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
SINGULAR LIMITS FOR 2-DIMENSIONAL ELLIPTIC PROBLEMS INVOLVING EXPONENTIAL NONLINEARITIES WITH SUB-QUADRATIC CONVECTION TERM
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 537-557
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
On Eells-Sampson’s existence theorem for harmonic maps via exponentially harmonic maps
-
- Journal:
- Nagoya Mathematical Journal / Volume 201 / March 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 133-146
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Multiple Solutions for a Class of Neumann Elliptic Problems on Compact Riemannian Manifolds with Boundary
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 674-683
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
Coupled Vortex Equations on Complete Kähler Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 3 / 01 September 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-480
- Print publication:
- 01 September 2008
-
- Article
-
- You have access
- Export citation
A Weighted
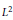 ${{L}^{2}}$ -Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
${{L}^{2}}$ -Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 943-965
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation