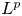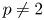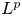1. Introduction
Let $(M,g)$![]() be a Riemannian manifold with associated Riemannian measure $\mu$
be a Riemannian manifold with associated Riemannian measure $\mu$![]() and denote by $\Delta$
and denote by $\Delta$![]() its negative definite Laplace–Beltrami operator (so that $\Delta = {\partial ^2}/{\partial x^2}$
its negative definite Laplace–Beltrami operator (so that $\Delta = {\partial ^2}/{\partial x^2}$![]() on $\mathbb {R}$
on $\mathbb {R}$![]() ). In the following, unless otherwise specified, all function spaces are understood over the real numbers.
). In the following, unless otherwise specified, all function spaces are understood over the real numbers.
Given a potential $V\in L^1_{\textrm {loc}}(M)$![]() and a family of functions $\mathcal {S}\subseteq L^1_{\textrm {loc}}(M)$
and a family of functions $\mathcal {S}\subseteq L^1_{\textrm {loc}}(M)$![]() , we say that the $\mathcal {S}$
, we say that the $\mathcal {S}$![]() positivity preserving property holds in $M$
positivity preserving property holds in $M$![]() for the operator $-\Delta +V$
for the operator $-\Delta +V$![]() if for every $u\in \mathcal {S}$
if for every $u\in \mathcal {S}$![]()
where the first inequality is understood in the sense of distributions. Recall that a function $u\in L^1_{\textrm {loc}}(M)$![]() satisfies $(-\Delta +V)u\geq 0$
satisfies $(-\Delta +V)u\geq 0$![]() (resp. $\leq 0$
(resp. $\leq 0$![]() ) in the sense of distributions if
) in the sense of distributions if
for every $0\leq \psi \in C_c^\infty (M)$![]() .
.
The positivity preservation for Schrödinger operators has been extensively studied in recent years. This definition was introduced by Güneysu in the paper [Reference Güneysu9] for the differential operator $-\Delta +1$![]() , although the property first appeared in [Reference Kato18] and [Reference Braverman, Milatovic and Shubin6]. In particular, in [Reference Braverman, Milatovic and Shubin6] the authors proved that the $L^2(M)$
, although the property first appeared in [Reference Kato18] and [Reference Braverman, Milatovic and Shubin6]. In particular, in [Reference Braverman, Milatovic and Shubin6] the authors proved that the $L^2(M)$![]() positivity preserving property for $-\Delta +1$
positivity preserving property for $-\Delta +1$![]() implies the essential self-adjointness of any operator $-\Delta +V$
implies the essential self-adjointness of any operator $-\Delta +V$![]() with $0\leq V \in L^2_{\textrm {loc}}(M)$
with $0\leq V \in L^2_{\textrm {loc}}(M)$![]() . Since this type of operators are known to be essentially self-adjoints on complete manifolds (see [Reference Braverman, Milatovic and Shubin6, Reference Shubin29]), Braverman, Milatovic and Shubin conjectured that the differential operator $(-\Delta +1)$
. Since this type of operators are known to be essentially self-adjoints on complete manifolds (see [Reference Braverman, Milatovic and Shubin6, Reference Shubin29]), Braverman, Milatovic and Shubin conjectured that the differential operator $(-\Delta +1)$![]() must satisfy the $L^2(M)$
must satisfy the $L^2(M)$![]() positivity preservation on every complete Riemannian manifold. This assertion has been popularized under the name of BMS conjecture from the names of the three authors [Reference Güneysu11].
positivity preservation on every complete Riemannian manifold. This assertion has been popularized under the name of BMS conjecture from the names of the three authors [Reference Güneysu11].
The BMS conjecture has been addressed by several authors, possibly considering additional assumptions on the geometry of the manifold at hand. See, for instance, [Reference Bianchi and Setti3, Reference Braverman, Milatovic and Shubin6, Reference Güneysu9, Reference Güneysu10, Reference Kato16, Reference Marini and Veronelli19]. Recently, it has been proved in the positive by Pigola, Valtorta and the second author in [Reference Pigola, Valtorta and Veronelli24] (see also [Reference Güneysu, Pigola, Stollmann and Veronelli13] for a generalization to non-smooth Dirichlet spaces). Using a monotonic approximation argument and some regularity results for subharmonic distributions, they proved that on every complete Riemannian manifold the operator $-\Delta +1$![]() satisfies the $L^p(M)$
satisfies the $L^p(M)$![]() positivity preserving property for any $p\in (1,+\infty )$
positivity preserving property for any $p\in (1,+\infty )$![]() .
.
Regarding the cases $p=1$![]() and $p=+\infty$
and $p=+\infty$![]() , without further assumptions the $L^p(M)$
, without further assumptions the $L^p(M)$![]() positivity preservation property for the operator $-\Delta +1$
positivity preservation property for the operator $-\Delta +1$![]() in general might fail even for complete manifolds. In this respect, in the recent work [Reference Bisterzo and Marini5] the first author and Marini determined
in general might fail even for complete manifolds. In this respect, in the recent work [Reference Bisterzo and Marini5] the first author and Marini determined
• that the $L^\infty (M)$
 positivity preserving property is equivalent to the stochastic completeness of the manifold (and thus unrelated to the geodesic completeness);
positivity preserving property is equivalent to the stochastic completeness of the manifold (and thus unrelated to the geodesic completeness);• the optimality of Theorem II in [Reference Marini and Veronelli19], which states that geodesic completeness and $\text {Ric}(x)\geq -C r^2(x)$
 outside a compact set imply the $L^1$
outside a compact set imply the $L^1$ positivity preservation for the operator.
positivity preservation for the operator.
The $L^p$![]() -positivity preserving property for more general Schrödinger operators $-\Delta + V$
-positivity preserving property for more general Schrödinger operators $-\Delta + V$![]() acting on complete Riemannian manifolds has been considered independently in the recent works [Reference Alias, Colombo and Rigoli1, Reference Bisterzo, Farina and Pigola4]. In particular, in this latter article the authors established on the one hand the positivity preserving property for a class of $L^p_{\textrm {loc}}(M)$
acting on complete Riemannian manifolds has been considered independently in the recent works [Reference Alias, Colombo and Rigoli1, Reference Bisterzo, Farina and Pigola4]. In particular, in this latter article the authors established on the one hand the positivity preserving property for a class of $L^p_{\textrm {loc}}(M)$![]() functions whose $L^p(M)$
functions whose $L^p(M)$![]() norm over geodesic balls satisfies a certain growth condition. On the other hand, for $p\in (1,+\infty )$
norm over geodesic balls satisfies a certain growth condition. On the other hand, for $p\in (1,+\infty )$![]() , they successfully dealt with differential operators of the form $-\Delta +V$
, they successfully dealt with differential operators of the form $-\Delta +V$![]() , where $0\leq V\in L^1_{\textrm {loc}}(M)$
, where $0\leq V\in L^1_{\textrm {loc}}(M)$![]() may decay to 0 at infinity.
may decay to 0 at infinity.
In a different direction, in [Reference Pigola, Valtorta and Veronelli24] the authors also managed to prove that the $L^p(M)$![]() positivity preservation for the operator $-\Delta +1$
positivity preservation for the operator $-\Delta +1$![]() is stable by removing from a complete manifold a possibly singular subset satisfying certain Hausdorff co-dimension or uniform Minkowski-type conditions. As a consequence, they showed the essential self-adjointness in $L^2(M)$
is stable by removing from a complete manifold a possibly singular subset satisfying certain Hausdorff co-dimension or uniform Minkowski-type conditions. As a consequence, they showed the essential self-adjointness in $L^2(M)$![]() of Schrödinger operators of the form $-\Delta + V$
of Schrödinger operators of the form $-\Delta + V$![]() for lower bounded potential $V\in L^2_{\textrm {loc}}(M)$
for lower bounded potential $V\in L^2_{\textrm {loc}}(M)$![]() , as well as the analogous spectral counterparts in $L^p(M)$
, as well as the analogous spectral counterparts in $L^p(M)$![]() , that is the fact that $C^\infty _c(M)$
, that is the fact that $C^\infty _c(M)$![]() is an operator core for the Schrödinger operator; see §4 for more details.
is an operator core for the Schrödinger operator; see §4 for more details.
The search for sufficient conditions to the validity of the essential self-adjointness of Schrödinger operators has been widely studied over the years. In the case of complete manifolds, let us mention at least [Reference Güneysu9, Reference Güneysu and Post14, Reference Kato17, Reference Milatovic21, Reference Milatovic22, Reference Shubin28, Reference Shubin29]. In the incomplete case, the essential self-adjointness of the Laplace–Beltrami operator (i.e. when $V=0$![]() ) was first investigated by Colin de Verdière and Masamune [Reference Colin de Verdière8, Reference Masammune20] when the singularity has integer codimension, and by Hinz, Masamune and Suzuki in the recent [Reference Hinz, Masamune and Suzuki15] in which the removed compact set may have non-integer codimension.
) was first investigated by Colin de Verdière and Masamune [Reference Colin de Verdière8, Reference Masammune20] when the singularity has integer codimension, and by Hinz, Masamune and Suzuki in the recent [Reference Hinz, Masamune and Suzuki15] in which the removed compact set may have non-integer codimension.
On the other hand, in [Reference Milatovic and Truc23] Milatovic and Truc adopted a different point of view in the study of the essential self-adjointness in $L^2(M)$![]() of Schrödinger operators of the form $-\Delta + V$
of Schrödinger operators of the form $-\Delta + V$![]() . Namely, they considered geodesically incomplete manifolds without requiring any assumption on the geometry of $M$
. Namely, they considered geodesically incomplete manifolds without requiring any assumption on the geometry of $M$![]() , and in particular on the codimension of the Cauchy boundary. The price to pay is a much stronger restriction on the potential $V$
, and in particular on the codimension of the Cauchy boundary. The price to pay is a much stronger restriction on the potential $V$![]() , which is required to explose at least quadratically near the Cauchy boundary of $M$
, which is required to explose at least quadratically near the Cauchy boundary of $M$![]() ; see [Reference Milatovic and Truc23, Theorem 3] for a precise statement. In view of the results alluded to above, it is thus natural to speculate that an intermediate control on the behaviour of the potential near the boundary can be combined with an intermediate bound on the codimension of the Cauchy boundary, to get assumptions which, in a sense, interpolate between the ones in [Reference Milatovic and Truc23] and in [Reference Pigola, Valtorta and Veronelli24]. This is the content of theorem 3.2.
; see [Reference Milatovic and Truc23, Theorem 3] for a precise statement. In view of the results alluded to above, it is thus natural to speculate that an intermediate control on the behaviour of the potential near the boundary can be combined with an intermediate bound on the codimension of the Cauchy boundary, to get assumptions which, in a sense, interpolate between the ones in [Reference Milatovic and Truc23] and in [Reference Pigola, Valtorta and Veronelli24]. This is the content of theorem 3.2.
As explained above, the approach to the essential self-adjointness through the $L^2(M)$![]() positivity preservation that we adopted here naturally generalizes to the $L^p(M)$
positivity preservation that we adopted here naturally generalizes to the $L^p(M)$![]() setting. We formalize this abstract phenomenon in theorem 4.17. As a concrete instance, in theorem 4.14 we prove that $C^\infty _c(M)$
setting. We formalize this abstract phenomenon in theorem 4.17. As a concrete instance, in theorem 4.14 we prove that $C^\infty _c(M)$![]() is an operator core in $L^p(M)$
is an operator core in $L^p(M)$![]() for the Schrödinger operator $-\Delta +V$
for the Schrödinger operator $-\Delta +V$![]() under assumptions on the smallness of the Minkowski dimension of the Cauchy boundary and on the growth of the potential $V$
under assumptions on the smallness of the Minkowski dimension of the Cauchy boundary and on the growth of the potential $V$![]() near the boundary.
near the boundary.
The paper is organized as follows. In §2 we prove the $L^p(M)$![]() positivity preserving property for operators of the form $-\Delta +V$
positivity preserving property for operators of the form $-\Delta +V$![]() , with $0\leq V\in L^\infty _{\textrm {loc}}(M)$
, with $0\leq V\in L^\infty _{\textrm {loc}}(M)$![]() having suitable lower bounds, which act on (possibly incomplete) Riemannian manifolds whose Cauchy boundary satisfies a Minkowski-type condition; see theorem 2.1. Following the heuristic described above, in §3 and 4 we apply the positivity preserving property just obtained in order to prove respectively that this class of operators on $C^\infty _c(M)$
having suitable lower bounds, which act on (possibly incomplete) Riemannian manifolds whose Cauchy boundary satisfies a Minkowski-type condition; see theorem 2.1. Following the heuristic described above, in §3 and 4 we apply the positivity preserving property just obtained in order to prove respectively that this class of operators on $C^\infty _c(M)$![]() are essentially self-adjoint in $L^2(M)$
are essentially self-adjoint in $L^2(M)$![]() and that $C^\infty _c(M)$
and that $C^\infty _c(M)$![]() is an operator core for the maximal $p$
is an operator core for the maximal $p$![]() -extension of $-\Delta +V$
-extension of $-\Delta +V$![]() . These results are stated in theorem 3.2 and in theorem 4.14.
. These results are stated in theorem 3.2 and in theorem 4.14.
2. $L^p(M)$ positivity preservation
positivity preservation
This section is aimed at proving the following
Theorem 2.1 Let $(N,h)$![]() be a complete Riemannian manifold and define $M:=N\setminus K$
be a complete Riemannian manifold and define $M:=N\setminus K$![]() , where $K\subset N$
, where $K\subset N$![]() is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$
is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$![]() is such that
is such that
where $C\in [0,1]$![]() and $m\in \{0,2\}$
and $m\in \{0,2\}$![]() are positive constants and $r(x):=d^N(x,K)$
are positive constants and $r(x):=d^N(x,K)$![]() is the distance function from $K$
is the distance function from $K$![]() . Fix $p\in (1,+\infty )$
. Fix $p\in (1,+\infty )$![]() and suppose there exist two positive constants $E\geq 1$
and suppose there exist two positive constants $E\geq 1$![]() and
and
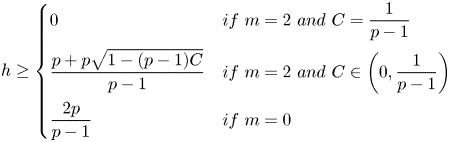
so that
where
Then the differential operator $-\Delta +V$![]() has the $L^p(M)$
has the $L^p(M)$![]() positivity preserving property.
positivity preserving property.
Remark 2.2 Reasoning as in [Reference Pigola, Valtorta and Veronelli24, Section 5], it is easy to see that theorem 2.1, and consequently theorems 3.2 and 4.14, hold as well if $N$![]() is assumed to be $q$
is assumed to be $q$![]() -parabolic for some $q\ge {2p}/{(p-1)}$
-parabolic for some $q\ge {2p}/{(p-1)}$![]() , but possibly incomplete.
, but possibly incomplete.
Remark 2.3 As explained in the introduction, the case $m=0$![]() recovers a result obtained in [Reference Pigola, Valtorta and Veronelli24].
recovers a result obtained in [Reference Pigola, Valtorta and Veronelli24].
2.1. Preliminary results
In order to prove theorem 2.1 we need two fundamental tools. The first is the classical Brezis–Kato inequality. We refer to [Reference Brezis7, Reference Ponce25] for the Euclidean result and to [Reference Pigola, Valtorta and Veronelli24] for the Riemannian version.
Proposition 2.4 (Brezis–Kato inequality)
Let $(M,g)$![]() be a Riemannian manifold and $V\!$
be a Riemannian manifold and $V\!$![]() a measurable function on $M$
a measurable function on $M$![]() .
.
If $u\in L^1_{\textrm {loc}}(M)$![]() is so that $Vu\in L^1_{\textrm {loc}}(M)$
is so that $Vu\in L^1_{\textrm {loc}}(M)$![]() and satisfies $(-\Delta +V)u\leq 0$
and satisfies $(-\Delta +V)u\leq 0$![]() in the sense of distributions, then
in the sense of distributions, then
where $u^+(x):=\max \{u(x),0\}$![]() .
.
The second ingredient is the regularity result contained in [Reference Bisterzo, Farina and Pigola4, Proposition 2.2]. Initially stated for complete Riemannian manifolds, we stress that its original proof recovers in fact also the case of incomplete Riemannian manifolds. Before stating this result, we recall that the negative part of a real-valued function, denoted with $u^-$![]() , is defined as
, is defined as
Using the above notation, the mentioned regularity result states what follows.
Proposition 2.5 Let $(M,g)$![]() be a (possibly incomplete) Riemannian manifolds and $0\leq V\in L^\infty _{\textrm {loc}}(M)$
be a (possibly incomplete) Riemannian manifolds and $0\leq V\in L^\infty _{\textrm {loc}}(M)$![]() .
.
If $u\in L^1_{\textrm {loc}}(M)$![]() satisfies $(-\Delta +V)u\geq 0$
satisfies $(-\Delta +V)u\geq 0$![]() in the sense of distributions, then
in the sense of distributions, then
(1) $u^- \in L^\infty _{\textrm {loc}}(M)$
 and $(u^-)^{p/2}\in W^{1,2}_{\textrm {loc}}(M)$
and $(u^-)^{p/2}\in W^{1,2}_{\textrm {loc}}(M)$ for every $p\in (1,+\infty )$
for every $p\in (1,+\infty )$ ;
;(2) for every $p\in (1,+\infty )$
 the function $u^-$
the function $u^-$ satisfies
(2.3)\begin{equation} (p-1) \int_M V(u^-)^p \varphi^2 \text{d}\mu \leq \int_M (u^-)^p |\nabla \varphi|^2 \text{d}\mu \end{equation}for every $0\leq \varphi \in C_c^{0,1}(M)$
satisfies
(2.3)\begin{equation} (p-1) \int_M V(u^-)^p \varphi^2 \text{d}\mu \leq \int_M (u^-)^p |\nabla \varphi|^2 \text{d}\mu \end{equation}for every $0\leq \varphi \in C_c^{0,1}(M)$
 .
.
2.2. Positivity preservation
In this subsection, we will prove the positivity preserving property stated as theorem 2.1, which is based on inequality (2.3). To this aim, let $R>\epsilon >2\eta > 0$![]() and $\delta >0$
and $\delta >0$![]() and consider the following real function $\psi :\mathbb {R}_{\geq 0}\to \mathbb {R}_{\geq 0}$
and consider the following real function $\psi :\mathbb {R}_{\geq 0}\to \mathbb {R}_{\geq 0}$![]()

Let $(N,g)$![]() be a complete Riemannian manifold and define $M:=N\setminus K$
be a complete Riemannian manifold and define $M:=N\setminus K$![]() , where $K\subset N$
, where $K\subset N$![]() is a compact subset. Denote with $r(x):=d^N(x,K)$
is a compact subset. Denote with $r(x):=d^N(x,K)$![]() the distance function from $K$
the distance function from $K$![]() and consider the following cut-off function
and consider the following cut-off function
In particular, $\varphi _{R,\epsilon,\eta }$![]() can be extended to 0 in $K$
can be extended to 0 in $K$![]() , obtaining $\varphi _{R,\epsilon,\eta }\in C^{0,1}_c(N)$
, obtaining $\varphi _{R,\epsilon,\eta }\in C^{0,1}_c(N)$![]() .
.
We are now in a position to prove the $L^p(M)$![]() positivity preserving property.
positivity preserving property.
Proof Proof of theorem 2.1
Let $v\in L^p(M)$![]() be a solution to $(-\Delta +V)v\geq 0$
be a solution to $(-\Delta +V)v\geq 0$![]() and denote $u:=v^- \geq 0$
and denote $u:=v^- \geq 0$![]() . Fix $\delta >0$
. Fix $\delta >0$![]() and for $0\leq 2\eta <\epsilon < R$
and for $0\leq 2\eta <\epsilon < R$![]() consider the function $\varphi _{R,\epsilon,\eta }$
consider the function $\varphi _{R,\epsilon,\eta }$![]() .
.
Step 1. We start by supposing that the support of $v$![]() is compact in $N$
is compact in $N$![]() . Fix $s\in (1,p]$
. Fix $s\in (1,p]$![]() . By applying (2.3) to the test functions $\varphi _{R,\epsilon,\eta }$
. By applying (2.3) to the test functions $\varphi _{R,\epsilon,\eta }$![]() , we get
, we get
On the one hand, we have

while, on the other hand, choosing $R$![]() big enough so that the support of $u$
big enough so that the support of $u$![]() is contained in $B_R$
is contained in $B_R$![]() ,
,

By putting together the previous inequalities, we obtain

where the last inequality follows from the Hölder inequality. Hence, recalling that the support of $u$![]() is contained in $B_R$
is contained in $B_R$![]() ,
,
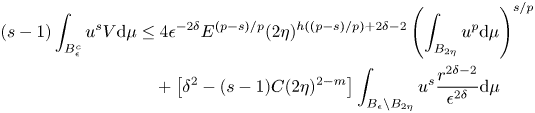
for every $s\in (1,p]$![]() . In our assumptions, we can choose $\delta$
. In our assumptions, we can choose $\delta$![]() and $s$
and $s$![]() so that
so that
and
for every $h$![]() satisfying (2.1). Indeed, following a case-by-case analysis:
satisfying (2.1). Indeed, following a case-by-case analysis:
• $m=2$
 and $C={1}/{(p-1)}$
and $C={1}/{(p-1)}$ : in this case we can just choose $s=p$
: in this case we can just choose $s=p$ and $\delta =1$
and $\delta =1$ , so that (2.6) is trivially satisfied for every $h\ge 0$
, so that (2.6) is trivially satisfied for every $h\ge 0$ .
.• $m=2$
 and $C\in (0,{1}/{(p-1)})$
and $C\in (0,{1}/{(p-1)})$ : in this case we choose $\delta = {pC}/{h}$
: in this case we choose $\delta = {pC}/{h}$ and $s=1+({\delta ^2}/{C})$
and $s=1+({\delta ^2}/{C})$ . Observing that
\begin{align*} h \frac{p-s}{p}+2\delta-2\geq 0 \quad & \Leftrightarrow \quad h(p-s)+2p\delta-2p\geq 0 \\ & \Leftrightarrow \quad h\left(p-1-\frac{\delta^2}{C} \right)+2p\delta-2p\geq 0\\ & \Leftrightarrow \quad h^2(p-1)-h2p+p^2 C \geq 0, \end{align*}by the fact that $C<{1}/{(p-1)}$
. Observing that
\begin{align*} h \frac{p-s}{p}+2\delta-2\geq 0 \quad & \Leftrightarrow \quad h(p-s)+2p\delta-2p\geq 0 \\ & \Leftrightarrow \quad h\left(p-1-\frac{\delta^2}{C} \right)+2p\delta-2p\geq 0\\ & \Leftrightarrow \quad h^2(p-1)-h2p+p^2 C \geq 0, \end{align*}by the fact that $C<{1}/{(p-1)}$
 it follows
\begin{align*} & \Delta=4p^2-4p^2(p-1)C\geq 0\\ & \Rightarrow \quad h^2(p-1)-h2p+p^2 C \geq 0 \quad \forall h\geq \frac{p+p\sqrt{1-(p-1)C}}{p-1}\\ & \Rightarrow \quad h \frac{p-s}{p}+2\delta-2\geq 0\quad \forall h\geq \frac{p+p\sqrt{1-(p-1)C}}{p-1}, \end{align*}implying (2.6) when $\eta$
it follows
\begin{align*} & \Delta=4p^2-4p^2(p-1)C\geq 0\\ & \Rightarrow \quad h^2(p-1)-h2p+p^2 C \geq 0 \quad \forall h\geq \frac{p+p\sqrt{1-(p-1)C}}{p-1}\\ & \Rightarrow \quad h \frac{p-s}{p}+2\delta-2\geq 0\quad \forall h\geq \frac{p+p\sqrt{1-(p-1)C}}{p-1}, \end{align*}implying (2.6) when $\eta$
 is small enough.
is small enough.• $m=0$
 : we choose $\delta ={pC(2\eta )^{2}}/{h}$
: we choose $\delta ={pC(2\eta )^{2}}/{h}$ and $s=1+({\delta ^2}/{C(2\eta )^{2}})$
and $s=1+({\delta ^2}/{C(2\eta )^{2}})$ . As in the previous case
\begin{align*} h \frac{p-s}{p}+2\delta-2\geq 0 \quad & \Leftrightarrow \quad h(p-s)+2p\delta-2p\geq 0 \\ & \Leftrightarrow \quad h^2(p-1)-h2p+p^2C(2\eta)^{2}\geq 0 \end{align*}with
. As in the previous case
\begin{align*} h \frac{p-s}{p}+2\delta-2\geq 0 \quad & \Leftrightarrow \quad h(p-s)+2p\delta-2p\geq 0 \\ & \Leftrightarrow \quad h^2(p-1)-h2p+p^2C(2\eta)^{2}\geq 0 \end{align*}with \[ \Delta=4p^2-4p^2(p-1)C(2\eta)^{2}. \]Since we are interested in the limit as $\eta \to 0$
\[ \Delta=4p^2-4p^2(p-1)C(2\eta)^{2}. \]Since we are interested in the limit as $\eta \to 0$
 , we get
\[ h \frac{p-s}{p}+2\delta-2\geq 0 \quad \forall h\geq \frac{2p}{p-1} \]implying, again, (2.6).
, we get
\[ h \frac{p-s}{p}+2\delta-2\geq 0 \quad \forall h\geq \frac{2p}{p-1} \]implying, again, (2.6).
From (2.5) and (2.6), inequality (2.4) implies

Since this holds for any fixed $\epsilon >0$![]() , we get
, we get
which, together with the fact that $V>0$![]() and $u\geq 0$
and $u\geq 0$![]() , implies
, implies
Step 2. Now consider the general case where $v$![]() is not assumed to be compactly supported. Since $u:=v^- \in L^\infty _{\textrm {loc}}(M)$
is not assumed to be compactly supported. Since $u:=v^- \in L^\infty _{\textrm {loc}}(M)$![]() by proposition 2.5, it follows that $\left |\left | u \right | \right |_{L^\infty (B_\epsilon \setminus B_{2\eta })}<+\infty$
by proposition 2.5, it follows that $\left |\left | u \right | \right |_{L^\infty (B_\epsilon \setminus B_{2\eta })}<+\infty$![]() . Consider the function
. Consider the function

By proposition 2.4,

where the last inequality holds since $(\left |\left | u \right | \right |_{L^\infty (B_\epsilon \setminus B_{2\eta })}-u)\geq 0$![]() in $B_\epsilon \setminus B_{2\eta }$
in $B_\epsilon \setminus B_{2\eta }$![]() . Since $w\in L^p(M)$
. Since $w\in L^p(M)$![]() , by step 1,
, by step 1,
In particular,
As a consequence, by proposition 2.5 applied to the test function $\varphi _{R,\epsilon,\eta }$![]() , for any $s\in (1,p]$
, for any $s\in (1,p]$![]()

and as $R\to +\infty$![]() we get
we get

which implies

In particular, this is equivalent to

for any $s\in (1,p]$![]() . Observing that $0\leq u^{{p}/s})\in L^p(B_\epsilon )$
. Observing that $0\leq u^{{p}/s})\in L^p(B_\epsilon )$![]() thanks to (2.7), under the assumptions (2.2) and (2.1) we can apply the argument presented in previous step obtaining that $u\equiv 0$
thanks to (2.7), under the assumptions (2.2) and (2.1) we can apply the argument presented in previous step obtaining that $u\equiv 0$![]() in $B_\epsilon ^c$
in $B_\epsilon ^c$![]() . By the arbitrariness of $\epsilon >0$
. By the arbitrariness of $\epsilon >0$![]() , we get $u\equiv 0$
, we get $u\equiv 0$![]() and so $v$
and so $v$![]() is nonnegative.
is nonnegative.
3. Essential self-adjointness
As mentioned above, the positivity preserving property arises naturally when one deals with the self-adjointness of linear operators. In particular, as we are going to see, as soon as the $L^2$![]() positivity preserving property holds for a certain class of Schrödinger operators, then these operators turn out to be essentially self-adjoint.
positivity preserving property holds for a certain class of Schrödinger operators, then these operators turn out to be essentially self-adjoint.
3.1. Standard notions and results about self-adjointness
We recall some basic definitions about operators defined over Hilbert spaces. For further details, we refer to [Reference Kato18, Reference Reed and Simon26, Reference Reed and Simon27].
Let $H$![]() be an Hilbert space with respect to the scalar product $(\cdot,\cdot )_H$
be an Hilbert space with respect to the scalar product $(\cdot,\cdot )_H$![]() , and $T:D(T)\subseteq H\to H$
, and $T:D(T)\subseteq H\to H$![]() an unbounded linear operator, where $D(T)$
an unbounded linear operator, where $D(T)$![]() is the domain of $T$
is the domain of $T$![]() . From now on we will consider densely defined linear operators. The adjoint of $T$
. From now on we will consider densely defined linear operators. The adjoint of $T$![]() , denoted with $T^*$
, denoted with $T^*$![]() , is defined as the linear operator on $H$
, is defined as the linear operator on $H$![]() whose domain is
whose domain is
and whose action is given by $T^*v=w$![]() . In particular, by definition
. In particular, by definition
The operator $T$![]() is said to be
is said to be
• symmetric if
\[ (Tu,v)_H=(u,Tv)_H\quad \forall u,v\in D(T) \]or, equivalently, if $T\subseteq T^*$
 ;
;• self-adjoint if $T=T^*$
 , that is, if $T$
, that is, if $T$ is symmetric and $D(T)=D(T^*)$
is symmetric and $D(T)=D(T^*)$ ;
;• essentially self-adjoint if $T$
 is symmetric and its closure $\overline {T}$
is symmetric and its closure $\overline {T}$ (defined as the operator whose graph is the closure of the graph of $T$
(defined as the operator whose graph is the closure of the graph of $T$ ) is self-adjoint.
) is self-adjoint.
Remark 3.1 We stress that
• by definition, the adjoint of an operator is a closed operator. In particular, if $T$
 is symmetric (resp. self-adjoint), then $T$
is symmetric (resp. self-adjoint), then $T$ is closable (resp. closed);
is closable (resp. closed);• by an abstract fact ([Reference Kato18, Theorem 5.29]), $(T^*)^*=\overline {T}$
 ;
;• a symmetric operator $T$
 is essentially self-adjoint if and only if it has a unique self-adjoint extension (see [Reference Reed and Simon26, p. 256]).
is essentially self-adjoint if and only if it has a unique self-adjoint extension (see [Reference Reed and Simon26, p. 256]).
3.2. Essential self-adjointness
We now present an application of theorem 2.1 to the essential self-adjointness of Schrödinger operators.
Theorem 3.2 Let $(N,h)$![]() be a complete Riemannian manifold and define $M:=N\setminus K$
be a complete Riemannian manifold and define $M:=N\setminus K$![]() , where $K\subset N$
, where $K\subset N$![]() is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$
is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$![]() is such that
is such that
where $C\in [0,1]$![]() , $m\in \{0,2\}$
, $m\in \{0,2\}$![]() and $A$
and $A$![]() are positive constants and $r(x):=d^N(x,K)$
are positive constants and $r(x):=d^N(x,K)$![]() is the distance function from $K$
is the distance function from $K$![]() . Suppose there exist two positive constants $E\geq 1$
. Suppose there exist two positive constants $E\geq 1$![]() and
and
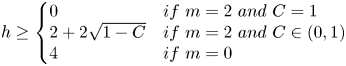
so that
Then the differential operator $-\Delta +V:C^\infty _c(M)\subset L^2(M) \to L^2(M)$![]() is essentially self-adjoint.
is essentially self-adjoint.
Remark 3.3 The case $m=2$![]() and $C=1$
and $C=1$![]() was previously obtained in [Reference Milatovic and Truc23] with a different approach, while the case $m=0$
was previously obtained in [Reference Milatovic and Truc23] with a different approach, while the case $m=0$![]() is already contained in [Reference Pigola, Valtorta and Veronelli24]. Here we recover with a unified point of view both sets of assumptions, as well as all the new intermediate cases $m=2$
is already contained in [Reference Pigola, Valtorta and Veronelli24]. Here we recover with a unified point of view both sets of assumptions, as well as all the new intermediate cases $m=2$![]() and $C\in (0,1)$
and $C\in (0,1)$![]() .
.
Proof. Let $\widetilde {V}=V+B>0$![]() . It is a standard fact (see [Reference Reed and Simon27, Theorem X.26]) that a necessary and sufficient condition for the operator $-\Delta +\widetilde {V}$
. It is a standard fact (see [Reference Reed and Simon27, Theorem X.26]) that a necessary and sufficient condition for the operator $-\Delta +\widetilde {V}$![]() to be essentially self-adjoint on the domain $C^\infty _c(M)$
to be essentially self-adjoint on the domain $C^\infty _c(M)$![]() is that the unique distributional solution $u\in L^2(M)$
is that the unique distributional solution $u\in L^2(M)$![]() to $(-\Delta +\widetilde {V})u=0$
to $(-\Delta +\widetilde {V})u=0$![]() is the constant null function. Hence, let $u\in L^2(M)$
is the constant null function. Hence, let $u\in L^2(M)$![]() be a distributional solution to $(-\Delta +\widetilde {V})u=0$
be a distributional solution to $(-\Delta +\widetilde {V})u=0$![]() : by theorem 2.1 applied both to $u$
: by theorem 2.1 applied both to $u$![]() and $-u$
and $-u$![]() it follows that $u=0$
it follows that $u=0$![]() . This means that
. This means that
and hence $-\Delta +\widetilde {V}$![]() is essentially self-adjoint on $C_c^\infty (M)$
is essentially self-adjoint on $C_c^\infty (M)$![]() . By the invariance of the essential self-adjointness with respect to potential translations (see [Reference Milatovic and Truc23, Proposition 4.1]), it follows that $-\Delta +V$
. By the invariance of the essential self-adjointness with respect to potential translations (see [Reference Milatovic and Truc23, Proposition 4.1]), it follows that $-\Delta +V$![]() is essentially self-adjoint on $C_c^\infty (M)$
is essentially self-adjoint on $C_c^\infty (M)$![]() , obtaining the claim.
, obtaining the claim.
Remark 3.4 We stress that the bound $2+2\sqrt {1-C}$![]() is sharp. Namely, for $h=3$
is sharp. Namely, for $h=3$![]() and for every $n\ge 3$
and for every $n\ge 3$![]() and $C<1-(h-2)^2/4=3/4$
and $C<1-(h-2)^2/4=3/4$![]() there exist a $C^2$
there exist a $C^2$![]() $n$
$n$![]() -dimensional Riemannian manifold $N$
-dimensional Riemannian manifold $N$![]() and a compact set $K\subset N$
and a compact set $K\subset N$![]() such that
such that
• $\mu (B_r(K))\leq E r^h$
 for $r$
for $r$ small enough and
small enough and• the equation $(-\Delta +C/r^2)u=0$
 admits an $L^2(M)$
admits an $L^2(M)$ solution, which in turn proves that $-\Delta + ({C}/{r^2}):C^\infty _c(M)\subset L^2(M) \to L^2(M)$
solution, which in turn proves that $-\Delta + ({C}/{r^2}):C^\infty _c(M)\subset L^2(M) \to L^2(M)$ is not essentially self-adjoint.
is not essentially self-adjoint.
Indeed, suppose first that $n=h=3$![]() and $C<3/4$
and $C<3/4$![]() . Let $N:=(\mathbb {R}_{\geq 0}\times _\sigma \mathbb {S}^2, \ \text {d}r+\sigma ^2 g^{\mathbb {S}^2})$
. Let $N:=(\mathbb {R}_{\geq 0}\times _\sigma \mathbb {S}^2, \ \text {d}r+\sigma ^2 g^{\mathbb {S}^2})$![]() be the model manifold with coordinates $(r,\theta )$
be the model manifold with coordinates $(r,\theta )$![]() associated to the warping function
associated to the warping function
where $b\in ( 1,\tfrac {3}{2})$![]() solves $C=b^2-b\in (0,\tfrac {3}{4})$
solves $C=b^2-b\in (0,\tfrac {3}{4})$![]() . Note that $\sigma '(0)=1$
. Note that $\sigma '(0)=1$![]() and $\sigma (0)=\sigma ''(0)=0$
and $\sigma (0)=\sigma ''(0)=0$![]() so that $N$
so that $N$![]() is $C^2$
is $C^2$![]() . Let $K=\{0\}$
. Let $K=\{0\}$![]() be the pole of the model manifold $N$
be the pole of the model manifold $N$![]() and define $M:=N\setminus K$
and define $M:=N\setminus K$![]() and $u:M\to \mathbb {R}$
and $u:M\to \mathbb {R}$![]() given by
given by
In particular, $u$![]() is a positive function satisfying
is a positive function satisfying
on $M$![]() . Moreover $u\in L^2(M)$
. Moreover $u\in L^2(M)$![]() since
since
which is integrable both around 0 and at $+\infty$![]() thanks to the choice of $b$
thanks to the choice of $b$![]() . Examples with $n>3=h$
. Examples with $n>3=h$![]() can be obtained by considering $N^3\times \mathbb {T}^{n-3}$
can be obtained by considering $N^3\times \mathbb {T}^{n-3}$![]() where $N^3$
where $N^3$![]() is as above, $\mathbb {T}^{n-3}$
is as above, $\mathbb {T}^{n-3}$![]() is a $(n-3)$
is a $(n-3)$![]() -dimensional torus, and $K=\{0\}\times \mathbb {T}^{n-3}$
-dimensional torus, and $K=\{0\}\times \mathbb {T}^{n-3}$![]() . We believe that similar counterexamples should exist also for non-integer $h\in (2,4)$
. We believe that similar counterexamples should exist also for non-integer $h\in (2,4)$![]() , even if in that case we expect explicit computations to be much more tricky.
, even if in that case we expect explicit computations to be much more tricky.
4. Operator core
The second application of theorem 2.1 we present is the generalization of theorem 3.2 to the context of $L^p(M)$![]() spaces with $p\neq 2$
spaces with $p\neq 2$![]() . Indeed, in this case a similar conclusion can be proved just replacing the self-adjointness with the property that $C_c^\infty (M)$
. Indeed, in this case a similar conclusion can be proved just replacing the self-adjointness with the property that $C_c^\infty (M)$![]() is an operator core in $L^p(M)$
is an operator core in $L^p(M)$![]() .
.
The general scheme we adopt will be summarized in the abstract result theorem 4.17 at the end of this section. This is surely well-known to the experts, and can be deduced from a number of references quoted in the introduction of this paper. However, we have not found it explicitly writen in the literature so that we decided to state it.
4.1. Standard notions and results about accretive operators
We start by recalling the following definition.
Definition 4.1 (Strongly continuous semigroup)
A family of bounded operators $\{T(t)\}_{t\in \mathbb {R}_{\geq 0}}$![]() defined over a Banach space $B$
defined over a Banach space $B$![]() is a strongly continuous semigroup if
is a strongly continuous semigroup if
• $T(0)=I$
 ;
;• $T(s)T(t)=T(s+t)$
 for all $s,t\in \mathbb {R}_{\geq 0}$
for all $s,t\in \mathbb {R}_{\geq 0}$ ;
;• for each $\psi \in B$
 the map $t\mapsto T(t)\psi$
the map $t\mapsto T(t)\psi$ is continuous.
is continuous.
A special class of such semigroups is given by the contraction semigroups. A strongly continuous semigroup $\{T(t)\}$![]() defined over a Banach space $B$
defined over a Banach space $B$![]() is said to be a contraction semigroup if
is said to be a contraction semigroup if
Here $\left |\left | \,\cdot\,\right | \right |_{}$![]() denotes the operator norm. The next proposition ([Reference Reed and Simon27, p. 237]) shows that any contraction semigroup can be ‘generated’ by a closed operator.
denotes the operator norm. The next proposition ([Reference Reed and Simon27, p. 237]) shows that any contraction semigroup can be ‘generated’ by a closed operator.
Proposition 4.2 Let $T(t)$![]() be a strongly continuous semigroup on a Banach space $B$
be a strongly continuous semigroup on a Banach space $B$![]() and set
and set
and
defined over $D(A):=\{\psi \in B\ :\ \lim _{t\to 0} A_t \psi \ \textit {exists}\}$![]() . Then, $A$
. Then, $A$![]() is closed and densely defined.
is closed and densely defined.
The operator $A$![]() is called the infinitesimal generator of $T(t)$
is called the infinitesimal generator of $T(t)$![]() . We will also say that $A$
. We will also say that $A$![]() generates $T(t)$
generates $T(t)$![]() and write $T(t)={\rm e}^{-tA}$
and write $T(t)={\rm e}^{-tA}$![]() .
.
In the remaining part of this subsection, we introduce the notions of accretive and maximal accretive operators. To this aim, we recall that given a Banach space $(B,\left |\left | \,\cdot\, \right | \right |_{B})$![]() and $\psi \in B$
and $\psi \in B$![]() , an element in its dual space $l\in B^*$
, an element in its dual space $l\in B^*$![]() is said to be a normalized tangent functional to $\psi$
is said to be a normalized tangent functional to $\psi$![]() if it satisfies
if it satisfies
Observe that by the Hahn–Banach theorem, each $\psi \in B$![]() has at least one normalized tangent functional.
has at least one normalized tangent functional.
Definition 4.3 (Accretive and $m$![]() -accretive operator)
-accretive operator)
A densely defined operator $A$![]() over a Banach space $B$
over a Banach space $B$![]() is said to be accretive if for any $\psi \in D(A)$
is said to be accretive if for any $\psi \in D(A)$![]() there exists a normalized tangent functional $l\in B^*$
there exists a normalized tangent functional $l\in B^*$![]() to $\psi$
to $\psi$![]() such that $l(A\psi )\geq 0$
such that $l(A\psi )\geq 0$![]() .
.
An accretive operator $A$![]() is said to be maximal accretive (or $m$
is said to be maximal accretive (or $m$![]() -accretive) if it has no proper accretive extensions.
-accretive) if it has no proper accretive extensions.
Remark 4.4 We stress that
• every accretive operator is closable;
• the closure of an accretive operator is again accretive.
As a consequence, every accretive operator has a smallest closed accretive extension. For a reference see [Reference Reed and Simon27, Section X.8].
Now we can state the fundamental criterion.
Theorem 4.5 (Fundamental criterion)
A closed operator $A$![]() on a Banach space $B$
on a Banach space $B$![]() is the generator of a contraction semigroup if and only if $A$
is the generator of a contraction semigroup if and only if $A$![]() is accretive and $\text {Ran}(\lambda _0+A)=B$
is accretive and $\text {Ran}(\lambda _0+A)=B$![]() for some $\lambda _0>0$
for some $\lambda _0>0$![]() .
.
Proof. We refer to [Reference Reed and Simon27, Theorem X.48].
Remark 4.6 We stress that
(1) by the Hille–Yosida theorem ([Reference Reed and Simon27, Theorem X.47a]), if $A$
 is the generator of a contraction semigroup, then the open half-line $(-\infty,0)$
is the generator of a contraction semigroup, then the open half-line $(-\infty,0)$ is contained in the resolvent of $A$
is contained in the resolvent of $A$ . In particular, it follows that $\text {Ran}(I+A)=B$
. In particular, it follows that $\text {Ran}(I+A)=B$ ;
;(2) the generators of contraction semigroups are maximal accretive since the condition $\text {Ran}(I+A)=B$
 implies that $A$
implies that $A$ has no proper accretive extensions. The converse ($A$
has no proper accretive extensions. The converse ($A$ maximal accretive implies $A$
maximal accretive implies $A$ generates a contraction semigroup) holds if $B$
generates a contraction semigroup) holds if $B$ is an Hilbert space but not in the general Banach case. See [Reference Reed and Simon27, p. 241].
is an Hilbert space but not in the general Banach case. See [Reference Reed and Simon27, p. 241].
4.2. Operator core
Let $V\in L^\infty _{\textrm {loc}}(M)$![]() and consider the differential operator $-\Delta +V$
and consider the differential operator $-\Delta +V$![]() . If $p\in (1,+\infty )$
. If $p\in (1,+\infty )$![]() , we define the operator $(-\Delta +V)_{p,{\rm max}}$
, we define the operator $(-\Delta +V)_{p,{\rm max}}$![]() associated to $-\Delta +V$
associated to $-\Delta +V$![]() by the formula
by the formula
with domain
and the operator $(-\Delta +V)_{p,{\rm min}}$![]() as
as
Observe that since $V\in L^p_{\textrm {loc}}(M)$![]() , then $C_c^\infty (M)\subset D((-\Delta +V)_{p,{\rm max}})$
, then $C_c^\infty (M)\subset D((-\Delta +V)_{p,{\rm max}})$![]() and hence the last definition makes sense.
and hence the last definition makes sense.
4.2.1. $\overline {(-\Delta +V)_{p,{\rm min}}}$ is $m$
is $m$ -accretive
-accretive
Following the strategy of the proof adopted by Milatovic in [Reference Milatovic22, Section 2], the next step consists in proving that $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() is $m$
is $m$![]() -accretive. To this aim, we first prove that this operator is accretive.
-accretive. To this aim, we first prove that this operator is accretive.
Lemma 4.7 Let $(M,g)$![]() be a (possibly incomplete) Riemannian manifold. Consider $0\leq V\in L^\infty _{\textrm {loc}} (M)$
be a (possibly incomplete) Riemannian manifold. Consider $0\leq V\in L^\infty _{\textrm {loc}} (M)$![]() and let $p\in (1,+\infty )$
and let $p\in (1,+\infty )$![]() .
.
Then, the operator $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() is accretive.
is accretive.
Proof. It follows by Lemma 2.1 and Remark 2.2 in [Reference Milatovic22]. These latter are stated for complete manifolds, however the completeness assumption is not used, as remarked in the proof of [Reference Güneysu9, Proposition 2.9 (b)].
From now on we consider a complete Riemannian manifold $(N,h)$![]() and define $M:=N\setminus K$
and define $M:=N\setminus K$![]() , where $K\subset N$
, where $K\subset N$![]() is a compact subset. Let $V\in L^\infty _{\textrm {loc}} (M)$
is a compact subset. Let $V\in L^\infty _{\textrm {loc}} (M)$![]() so that
so that
where $C\in [0,1]$![]() and $m\in \{0,2\}$
and $m\in \{0,2\}$![]() are positive constants and $r(x):=d^N(x,K)$
are positive constants and $r(x):=d^N(x,K)$![]() is the distance function from $K$
is the distance function from $K$![]() . Fix $p\in (1,+\infty )$
. Fix $p\in (1,+\infty )$![]() and suppose there exist two positive constants $E\geq 1$
and suppose there exist two positive constants $E\geq 1$![]() and
and

or

so that
In what follows we always assume to be in this setting.
Remark 4.8 We stress that in the present section we are requiring the validity of a condition stronger than the one of (2.1) for the two indices $p$![]() and $p'=p/(p-1)$
and $p'=p/(p-1)$![]() in order to obtain that both $\overline {(-\Delta +V)_{p,{\rm min}}}$
in order to obtain that both $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() and $\overline {(-\Delta +V)_{p',{\rm min}}}$
and $\overline {(-\Delta +V)_{p',{\rm min}}}$![]() are $m$
are $m$![]() -accretive. This latter will be used to ensure that the operator $(-\Delta +V)_{p,{\rm max}}$
-accretive. This latter will be used to ensure that the operator $(-\Delta +V)_{p,{\rm max}}$![]() is accretive too.
is accretive too.
Thanks to the validity of theorem 2.1, we are able to prove the next
Theorem 4.9 $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() generates a contraction semigroup on $L^p(M)$
generates a contraction semigroup on $L^p(M)$![]() . In particular, $\overline {(-\Delta +V)_{p,{\rm min}}}$
. In particular, $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() is $m$
is $m$![]() -accretive.
-accretive.
The proof of theorem 4.9 can be obtained verbatim by the one of [Reference Milatovic22, Theorem 1.3] just replacing Lemma 2.7 in [Reference Milatovic22] with lemma 4.10 below, which is a consequence of the validity of the positivity preserving property.
Lemma 4.10 If $\lambda >0$![]() , then $\text {Ran}((-\Delta +V)_{p,{\rm min}}+\lambda )$
, then $\text {Ran}((-\Delta +V)_{p,{\rm min}}+\lambda )$![]() is dense in $L^p(M)$
is dense in $L^p(M)$![]() .
.
Proof. Let $v\in L^{p'}(M)$![]() so that
so that
which is equivalent to the following distributional equality
Since by hypothesis $V\in L^p_{\textrm {loc}}(M)$![]() and $v\in L^{p'}(M)$
and $v\in L^{p'}(M)$![]() , by Hölder inequality $Vv\in L^1_{\textrm {loc}}(M)$
, by Hölder inequality $Vv\in L^1_{\textrm {loc}}(M)$![]() . Since $\Delta v=Vv+\lambda v$
. Since $\Delta v=Vv+\lambda v$![]() , we get $\Delta v \in L^1_{\textrm {loc}}(M)$
, we get $\Delta v \in L^1_{\textrm {loc}}(M)$![]() . By Kato's inequality
. By Kato's inequality
and hence
By theorem 2.1 it follows that $|v|\leq 0$![]() and hence $v=0$
and hence $v=0$![]() .
.
4.2.2. $(-\Delta +V)_{p,{\rm max}}$ is $m$
is $m$ -accretive.
-accretive.
After proving that $\overline {(-\Delta +V)_{p,{\rm min}}}$![]() is $m$
is $m$![]() -accretive, the next stage is to show the same property for the operator $(-\Delta +V)_{p,{\rm max}}$
-accretive, the next stage is to show the same property for the operator $(-\Delta +V)_{p,{\rm max}}$![]() . We proceed by introducing the following result contained in [Reference Güneysu10, Lemma I.25]
. We proceed by introducing the following result contained in [Reference Güneysu10, Lemma I.25]
Lemma 4.11 Let $p\in (1,+\infty )$![]() and $p'=p/(p-1)$
and $p'=p/(p-1)$![]() . Then
. Then
As a consequence, we get
Theorem 4.12 $(-\Delta +V)_{p,{\rm max}}$![]() generates a contraction semigroup on $L^p(M)$
generates a contraction semigroup on $L^p(M)$![]() . In particular, $(-\Delta +V)_{p,{\rm max}}$
. In particular, $(-\Delta +V)_{p,{\rm max}}$![]() is $m$
is $m$![]() -accretive.
-accretive.
Proof. The proof follows as in [Reference Güneysu and Pigola12, Theorem 5]. Indeed, by theorem 4.9 the operator $\overline {(-\Delta +V)_{p',{\rm min}}}$![]() generates a contraction semigroup and by lemma 4.11
generates a contraction semigroup and by lemma 4.11
Since adjoints of generators of contraction semigroups in reflexive Banach spaces again generate such semigroups [Reference Arendt2, p.138], it follows that $(-\Delta +V)_{p,{\rm max}}$![]() generates a contraction semigroup and thus is $m$
generates a contraction semigroup and thus is $m$![]() -accretive.
-accretive.
4.2.3. Main result.
Before proceeding with the main result of this section, we recall the following
Definition 4.13 Let $T$![]() be a closed operator over a Banach space $B$
be a closed operator over a Banach space $B$![]() . For any closable operator $S$
. For any closable operator $S$![]() such that $\overline {S}=T$
such that $\overline {S}=T$![]() , its domain $D(S)$
, its domain $D(S)$![]() is said to be a core of $T$
is said to be a core of $T$![]() .
.
In other words, $D\subset D(T)$![]() is a core of $T$
is a core of $T$![]() if and only if the set $\{(u,Tu)\ :\ u\in D\}$
if and only if the set $\{(u,Tu)\ :\ u\in D\}$![]() is dense in $\Gamma (T)$
is dense in $\Gamma (T)$![]() .
.
Theorem 4.14 Let $(N,h)$![]() be a complete Riemannian manifold and define $M:=N\setminus K$
be a complete Riemannian manifold and define $M:=N\setminus K$![]() , where $K\subset N$
, where $K\subset N$![]() is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$
is a compact subset. Assume that $V\in L^\infty _{\textrm {loc}} (M)$![]() is such that
is such that
where $C\in [0,1]$![]() , $m\in \{0,2\}$
, $m\in \{0,2\}$![]() and $A$
and $A$![]() are positive constants and $r(x):=d^N(x,K)$
are positive constants and $r(x):=d^N(x,K)$![]() is the distance function from $K$
is the distance function from $K$![]() . Fix $p\in (1,+\infty )$
. Fix $p\in (1,+\infty )$![]() and suppose there exist two positive constants $E\geq 1$
and suppose there exist two positive constants $E\geq 1$![]() and
and

or

so that
Then $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V)_{p,{\rm max}}$
is an operator core for $(-\Delta +V)_{p,{\rm max}}$![]() .
.
Proof. Let $\widetilde {V}=V+B>0$![]() . By theorems 4.9 and 4.12, both $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}$
. By theorems 4.9 and 4.12, both $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}$![]() and $(-\Delta +\widetilde {V})_{p,{\rm max}}$
and $(-\Delta +\widetilde {V})_{p,{\rm max}}$![]() are $m$
are $m$![]() -accretive. By the fact that $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}\subset (-\Delta +\widetilde {V})_{p,{\rm max}}$
-accretive. By the fact that $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}\subset (-\Delta +\widetilde {V})_{p,{\rm max}}$![]() and by the definition of $m$
and by the definition of $m$![]() -accretive operator, it follows that $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}=(-\Delta +\widetilde {V})_{p,{\rm max}}$
-accretive operator, it follows that $\overline {(-\Delta +\widetilde {V})_{p,{\rm min}}}=(-\Delta +\widetilde {V})_{p,{\rm max}}$![]() , obtaining that $C^\infty _c(M)$
, obtaining that $C^\infty _c(M)$![]() is an operator core for $(-\Delta +\widetilde {V})_{p,{\rm max}}$
is an operator core for $(-\Delta +\widetilde {V})_{p,{\rm max}}$![]() . By the invariance of this property with respect to potential translations (see remark 4.15 below), we get the claim.
. By the invariance of this property with respect to potential translations (see remark 4.15 below), we get the claim.
Remark 4.15 We observe that $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V)_{p,{\rm max}}$
is an operator core for $(-\Delta +V)_{p,{\rm max}}$![]() , then $C^\infty _c$
, then $C^\infty _c$![]() is an operator core also for $(-\Delta +V+\lambda )_{p,{\rm max}}$
is an operator core also for $(-\Delta +V+\lambda )_{p,{\rm max}}$![]() for every $\lambda \in \mathbb {R}$
for every $\lambda \in \mathbb {R}$![]() .
.
Indeed, suppose that $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V)_{p,{\rm max}}$
is an operator core for $(-\Delta +V)_{p,{\rm max}}$![]() , meaning that $\{(u,(-\Delta +V)u)\ :\ u\in C^\infty _c(M)\}$
, meaning that $\{(u,(-\Delta +V)u)\ :\ u\in C^\infty _c(M)\}$![]() is dense in $\Gamma ((-\Delta +V)_{p,{\rm max}})$
is dense in $\Gamma ((-\Delta +V)_{p,{\rm max}})$![]() . Fixed $\lambda \in \mathbb {R}$
. Fixed $\lambda \in \mathbb {R}$![]() , consider $(u,(-\Delta +V+\lambda )u)\in \Gamma ((-\Delta +V+\lambda )_{p,{\rm max}})$
, consider $(u,(-\Delta +V+\lambda )u)\in \Gamma ((-\Delta +V+\lambda )_{p,{\rm max}})$![]() and observe that
and observe that
and hence
By the fact that $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V)_{p,{\rm max}}$
is an operator core for $(-\Delta +V)_{p,{\rm max}}$![]() it follows that there exists $\{u_n\}_n\subset C^\infty _c(M)$
it follows that there exists $\{u_n\}_n\subset C^\infty _c(M)$![]() so that
so that
i.e.
implying that
(1) $\left |\left | u_n-u \right | \right |_{L^p(M)}\xrightarrow []{n}0$

(2) $\left |\left | (-\Delta +V)(u_n-u) \right | \right |_{L^p(M)}\xrightarrow []{n}0$
 .
.
Whence, by Minkowski inequality,

and hence $(-\Delta +V+\lambda )u_n\xrightarrow []{L^p(M)}(-\Delta +V+\lambda )u$![]() . So
. So
It follows that for every $\lambda \in \mathbb {R}$![]() the set $\{(u,(-\Delta +V+\lambda )u\ :\ u\in C^\infty _c(M)\}$
the set $\{(u,(-\Delta +V+\lambda )u\ :\ u\in C^\infty _c(M)\}$![]() is dense in $\Gamma ((-\Delta +V+\lambda )_{p,{\rm max}})$
is dense in $\Gamma ((-\Delta +V+\lambda )_{p,{\rm max}})$![]() and hence $C^\infty _c(M)$
and hence $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V+\lambda )_{p,{\rm max}}$
is an operator core for $(-\Delta +V+\lambda )_{p,{\rm max}}$![]() .
.
Remark 4.16 In case $p=2$![]() (and hence $p'=2$
(and hence $p'=2$![]() ), we recover the result contained in theorem 3.2. Indeed, under the assumptions of theorem 3.2, the condition
), we recover the result contained in theorem 3.2. Indeed, under the assumptions of theorem 3.2, the condition
means exactly that the operator $-\Delta +V$![]() is essentially self-adjoint on $C^\infty _c(M)$
is essentially self-adjoint on $C^\infty _c(M)$![]() .
.
4.3. Consequence of the above construction
As we can see from the previous discussion, the construction carried out in this section is guaranteed even under more general assumptions than those required in theorem 4.14. In fact, we can observe that for the proofs of theorems 4.9 and 4.12, which are the key results from which theorem 4.14 immediately follows, only the property of positivity preservation for the operator $-\Delta + V$![]() is required. As a direct consequence of this fact, we obtain a machinery that ensures that $C^\infty _c$
is required. As a direct consequence of this fact, we obtain a machinery that ensures that $C^\infty _c$![]() is an operator core for the $p$
is an operator core for the $p$![]() -maximal extension of a given Schrödinger operator as soon as the underlying manifold satisfies the positivity preservation for that operator for the index $p$
-maximal extension of a given Schrödinger operator as soon as the underlying manifold satisfies the positivity preservation for that operator for the index $p$![]() and for its dual $p'$
and for its dual $p'$![]() . We summarize this result in the following
. We summarize this result in the following
Theorem 4.17 Let $(M,g)$![]() be a (possibly) incomplete Riemannian manifold. Consider $0< V\in L^\infty _{\textrm {loc}}(M)$
be a (possibly) incomplete Riemannian manifold. Consider $0< V\in L^\infty _{\textrm {loc}}(M)$![]() and $p\in (1,+\infty )$
and $p\in (1,+\infty )$![]() and define $p'={p}/{(p-1)}$
and define $p'={p}/{(p-1)}$![]() .
.
If $(M,g)$![]() satisfies both the $L^p(M)$
satisfies both the $L^p(M)$![]() and $L^{p'}(M)$
and $L^{p'}(M)$![]() positivity preserving property for the operator $-\Delta +V$
positivity preserving property for the operator $-\Delta +V$![]() , then $C^\infty _c(M)$
, then $C^\infty _c(M)$![]() is an operator core for $(-\Delta +V)_{p,{\rm max}}$
is an operator core for $(-\Delta +V)_{p,{\rm max}}$![]() .
.
Acknowledgements
The authors wish to express their gratitude to Ognjen Milatovic for his valuable feedback on the content and structure of the present article. Special thanks are extended to Stefano Pigola for his careful reading of the initial versions of this work and for the insightful discussions regarding the main theorems presented. Lastly, the authors would like to thank the anonymous referee for the valuable suggestions that have enhanced the presentation of this work. All the authors are members of the INdAM-GNAMPA group.