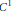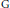Refine search
Actions for selected content:
9 results
Projectively and affinely invariant PDEs on hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 714-739
-
- Article
- Export citation
Families of similar simplices inscribed in most smoothly embedded spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GEOMETRIC SYMMETRY TECHNIQUES FOR PARTIAL DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 342-344
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Moving Frames for Lie Pseudo–Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 6 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1336-1386
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
Jet Modules
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-729
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation
INFINITE RELATIVE DETERMINACY OF SMOOTH FUNCTION GERMS WITH TRANSVERSE ISOLATED SINGULARITIES AND RELATIVE ŁOJASIEWICZ CONDITIONS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 29 March 2004, pp. 518-530
- Print publication:
- April 2004
-
- Article
- Export citation
On holomorphic maps with only fold singularities
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-184
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Affine structure on Weil bundles
-
- Journal:
- Nagoya Mathematical Journal / Volume 158 / December 2000
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-106
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Smooth Finite Dimensional Embeddings
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 3 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 585-615
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation
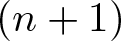
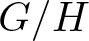
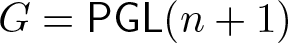
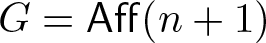
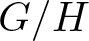
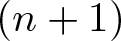
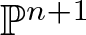
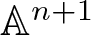
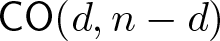
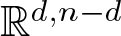

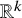
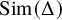
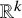

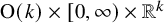
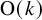
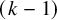
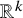
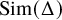
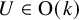
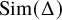
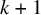
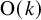
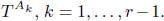 We deduce that
We deduce that 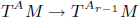 is an affine bundle for every manifold
is an affine bundle for every manifold 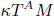 of contact elements of type
of contact elements of type