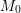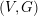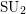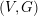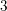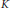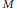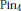Refine search
Actions for selected content:
7 results
Free torus actions and twisted suspensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symplectic quotients have symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 31 January 2020, pp. 613-646
- Print publication:
- March 2020
-
- Article
- Export citation
Erratum: Translation Groupoids and Orbifold Cohomology
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 851-853
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
Triangulation of the map of a G-manifold to its orbit space
-
- Journal:
- Nagoya Mathematical Journal / Volume 212 / December 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 159-195
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Translation Groupoids and Orbifold Cohomology
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 3 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 614-645
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation
Equivariant Cohomology of S 1-Actions on 4-Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 365-376
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation
The Classification of Pin4-Bundles over a 4-Complex
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 248-256
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation