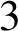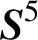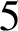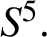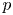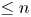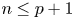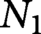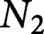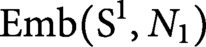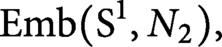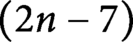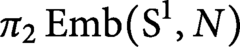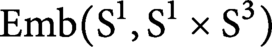Refine search
Actions for selected content:
12 results
On the finiteness of the classifying space of diffeomorphisms of reducible three manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graphing, homotopy groups of spheres, and spaces of long links and knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REIDEMEISTER’S THEOREM USING TRANSVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 356-367
- Print publication:
- April 2025
-
- Article
- Export citation
On inscribed trapezoids and affinely 3-regular maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 1024-1032
- Print publication:
- August 2024
-
- Article
- Export citation
Thurston’s fragmentation and c-principles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
 $3$-MANIFOLDS IN
$3$-MANIFOLDS IN 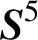 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
- Print publication:
- June 2022
-
- Article
- Export citation
Galois symmetries of knot spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 997-1021
- Print publication:
- May 2021
-
- Article
- Export citation
Spaces of knotted circles and exotic smooth structures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 August 2020, pp. 1-23
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Classification of knotted tori
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 549-567
- Print publication:
- April 2020
-
- Article
- Export citation
ON SELF-INTERSECTION INVARIANTS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 259-273
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
Concordance des nœuds de dimension 4
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 4 / 01 December 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-485
- Print publication:
- 01 December 2007
-
- Article
-
- You have access
- Export citation
Non-embeddings of the real flag manifolds RF (1, 1, n – 2)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-55
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation