A stereological formula for the Euler number involving projections of the set in thin parallel slabs is considered. Sufficient conditions for the validity of this formula are derived.

The main result provides mild conditions under which a closed, orientable, PL 4-manifold $N = N_1\,\#\,N_2$ with $\pi_1(N_e)$ residually finite ($e=1,2$) is a codimension-5 PL fibrator. The paper also presents a rich variety of conditions on a closed 4-manifold $N^4$ under which every PL map between manifolds, where the domain is orientable and all point inverses are copies of $N^4$, must be an approximate fibration.

We obtain a homotopy splitting of the forget control map for controlled homeomorphisms over closed manifolds of nonpositive curvature.

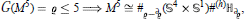
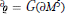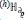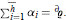In the present paper, we face the problem of classifying classes of orientable PL 5-manifolds M5 with h ≥ 1 boundary components, by making use of a combinatorial invariant called regular genusG(M5). In particular, a complete classification up to regular genus five is obtained: where denotes the regular genus of the boundary ∂M5 and denotes the connected sumof h ≥ 1 orientable 5-dimensional handlebodies 𝕐αi of genus αi ≥ 0 (i = 1, . . . ,h), so that .

Moreover, we give the following characterizations of orientable PL 5-manifolds M5 with boundary satisfying particular conditions related to the “gap” between G(M5) and either G(∂M5) or the rank of their fundamental group rk(π1(M5)): Further, the paper explains how the above results (together with other known properties of regular genus of PL manifolds) may lead to a combinatorial approach to 3-dimensional Poincaré Conjecture.

This paper defines three simplicial approximation properties for maps of 2-cells and 2-spheres into spaces, each providing homotopical tameness conditions on the approximating images. These are the general position properties used in the two main results. The first shows that a resolvable generalized 3-manifold is a genuine 3- manifold if and only if it has the weakest of these approximation properties as well as a mild 3-dimensional disjoint disks condition known as the Light Map Separation Property. The second shows a resolvable generalized 3-manifold to be a 3-manifold if and only if it satisfies the strongest of these approximation properties.

Uncountable collections of continua of dimension m embeddable in En are investigated, where the difference between m and n is not restricted to one. Collections of isometric copies of continua equivalent to Menger universal continua and collections of continua analogous to G. S. Young's Tn-sets are the main considerations.