Article contents
Classifying Pl 5-Manifolds by Regular Genus: The Boundary Case
Published online by Cambridge University Press: 20 November 2018
Abstract
In the present paper, we face the problem of classifying classes of orientable PL 5-manifolds M 5 with h ≥ 1 boundary components, by making use of a combinatorial invariant called regular genusG(M 5). In particular, a complete classification up to regular genus five is obtained: 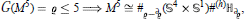 where
where 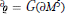 denotes the regular genus of the boundary ∂M 5 and
denotes the regular genus of the boundary ∂M 5 and 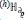 denotes the connected sumof h ≥ 1 orientable 5-dimensional handlebodies 𝕐αi of genus αi ≥ 0 (i = 1, . . . ,h), so that
denotes the connected sumof h ≥ 1 orientable 5-dimensional handlebodies 𝕐αi of genus αi ≥ 0 (i = 1, . . . ,h), so that 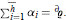 .
.
Moreover, we give the following characterizations of orientable PL 5-manifolds M 5 with boundary satisfying particular conditions related to the “gap” between G(M 5) and either G(∂M 5) or the rank of their fundamental group rk(π1(M 5)): 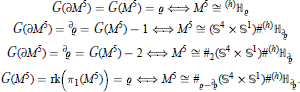 Further, the paper explains how the above results (together with other known properties of regular genus of PL manifolds) may lead to a combinatorial approach to 3-dimensional Poincaré Conjecture.
Further, the paper explains how the above results (together with other known properties of regular genus of PL manifolds) may lead to a combinatorial approach to 3-dimensional Poincaré Conjecture.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1997
References
- 9
- Cited by

