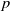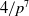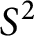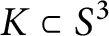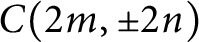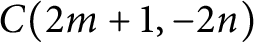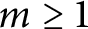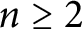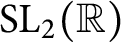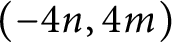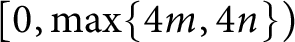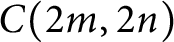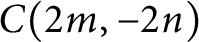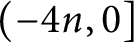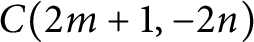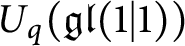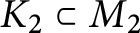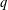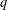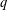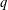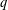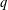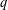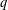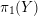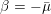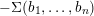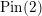Refine search
Actions for selected content:
63 results
On the Jones polynomial modulo primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 August 2023, pp. 730-734
- Print publication:
- September 2023
-
- Article
- Export citation
Primary decomposition in the smooth concordance group of topologically slice knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 August 2021, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIMENSION OF GROUPS THAT SATISFY CERTAIN CONDITIONS ON THEIR FINITE SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 04 November 2020, pp. 45-50
- Print publication:
- January 2022
-
- Article
- Export citation
On framings of links in 3-manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 752-764
- Print publication:
- December 2021
-
- Article
- Export citation
Rational cobordisms and integral homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 29 October 2020, pp. 1825-1845
- Print publication:
- September 2020
-
- Article
- Export citation
Left orderable surgeries of double twist knots II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 27 August 2020, pp. 624-637
- Print publication:
- September 2021
-
- Article
- Export citation
Kuperberg invariants for balanced sutured 3-manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1698-1742
- Print publication:
- December 2021
-
- Article
- Export citation
A splicing formula for the LMO invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1743-1770
- Print publication:
- December 2021
-
- Article
- Export citation
A FAST ALGORITHM FOR CALCULATING S-INVARIANTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 378-399
- Print publication:
- May 2021
-
- Article
- Export citation
Khovanov–Rozansky homology for infinite multicolored braids
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 1239-1277
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
ISOTOPY AND HOMEOMORPHISM OF CLOSED SURFACE BRAIDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 297-306
- Print publication:
- May 2021
-
- Article
- Export citation
GENERATORS, RELATIONS, AND HOMOLOGY FOR OZSVÁTH–SZABÓ’S KAUFFMAN-STATES ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 60-118
- Print publication:
- December 2021
-
- Article
- Export citation
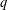 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 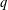 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
GAPS BETWEEN CONSECUTIVE UNTWISTING NUMBERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 February 2020, pp. 59-65
- Print publication:
- January 2021
-
- Article
- Export citation
The Chord Index, its Definitions, Applications, and Generalizations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 30 January 2020, pp. 597-621
- Print publication:
- June 2021
-
- Article
- Export citation
L-spaces, taut foliations, and graph manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 23 January 2020, pp. 604-612
- Print publication:
- March 2020
-
- Article
- Export citation
Pin(2)-equivariant Seiberg–Witten Floer homology of Seifert fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 199-250
- Print publication:
- February 2020
-
- Article
- Export citation
A NONDEGENERATE EXCHANGE MOVE ALWAYS PRODUCES INFINITELY MANY NONCONJUGATE BRAIDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 02 December 2019, pp. 205-208
- Print publication:
- September 2021
-
- Article
- Export citation
Johnson–Levine homomorphisms and the tree reduction of the LMO functor
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 291-325
- Print publication:
- March 2021
-
- Article
- Export citation
THE QUANDARY OF QUANDLES: A BOREL COMPLETE KNOT INVARIANT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 October 2019, pp. 262-277
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation