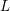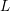Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shinjo, Reiko
and
Stoimenow, Alexander
2025.
Infinitely many non-conjugate braid representatives of links.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 7,
p.
107964.