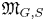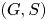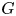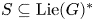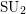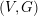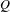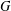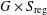Refine search
Actions for selected content:
27 results
A counterexample to Lagrangian Poincaré recurrence in dimension four
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 November 2025, pp. 2373-2379
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISTANCE FUNCTIONS ON CONVEX BODIES AND SYMPLECTIC TORIC MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-23
-
- Article
- Export citation
From Lagrangian products to toric domains via the Toda lattice
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 19 June 2025, pp. 365-384
- Print publication:
- February 2025
-
- Article
- Export citation
Stratification of the transverse momentum map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 518-585
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted nonlinear flag manifolds as coadjoint orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1664-1694
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hofer–Zehnder conjecture on weighted projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 87-108
- Print publication:
- January 2023
-
- Article
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symplectic reduction along a submanifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 18 October 2022, pp. 1878-1934
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HYDRODYNAMICAL HOMOTOPY CO-MOMENTUM MAP AND A MULTISYMPLECTIC INTERPRETATION OF HIGHER-ORDER LINKING NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 335-354
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Symplectic quotients have symplectic singularities
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 31 January 2020, pp. 613-646
- Print publication:
- March 2020
-
- Article
- Export citation
On geodesic flows with symmetries and closed magnetic geodesics on orbifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1480-1509
- Print publication:
- June 2020
-
- Article
- Export citation
AN EQUIVARIANT DESCRIPTION OF CERTAIN HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 207-214
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
MULTISYMPLECTIC VARIATIONAL INTEGRATORS FOR NONSMOOTH LAGRANGIAN CONTINUUM MECHANICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e19
-
- Article
-
- You have access
- Open access
- Export citation
Implosion for hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1592-1630
- Print publication:
- September 2013
-
- Article
- Export citation
Contact homology of good toric contact manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 304-334
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
The Toric Geometry of Triangulated Polygons in Euclidean Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 878-937
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
Revisiting Tietze–Nakajima: Local and Global Convexity for Maps
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 5 / 01 October 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 975-993
- Print publication:
- 01 October 2010
-
- Article
-
- You have access
- Export citation
The Fundamental Group of S 1-manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 5 / 01 October 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1082-1098
- Print publication:
- 01 October 2010
-
- Article
-
- You have access
- Export citation
Rigid subsets of symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 773-826
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Equivariant Cohomology of S 1-Actions on 4-Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 365-376
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation