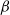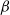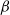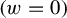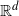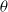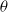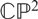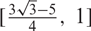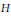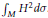Refine search
Actions for selected content:
33 results
Alexandrov sphere theorems for
 $ W^{2,n} $-hypersurfaces
$ W^{2,n} $-hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correspondence between Pestov and Weitzenböck identities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 02 May 2025, pp. 443-463
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity of Schur forms for strongly decomposably positive vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
- Export citation
On intersection probabilities of four lines inside a planar convex domain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 December 2022, pp. 504-527
- Print publication:
- June 2023
-
- Article
- Export citation
Crofton formulas in pseudo-Riemannian space forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 28 October 2022, pp. 1935-1979
- Print publication:
- October 2022
-
- Article
- Export citation
The
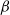 $\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
$\beta$-Delaunay tessellation: Description of the model and geometry of typical cells
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1252-1290
- Print publication:
- December 2022
-
- Article
- Export citation
Directed harmonic currents near non-hyperbolic linearizable singularities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 2228-2257
- Print publication:
- July 2023
-
- Article
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersections of random sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 131-151
- Print publication:
- March 2022
-
- Article
- Export citation
On point processes defined by angular conditions on Delaunay neighbors in the Poisson–Voronoi Tessellation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 952-965
- Print publication:
- December 2021
-
- Article
- Export citation
A NOTE ON THE CLASSIFICATION OF NONCOMPACT QUASI-EINSTEIN MANIFOLDS WITH VANISHING CONDITION ON THE WEYL TENSOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 07 May 2021, pp. 336-346
- Print publication:
- May 2022
-
- Article
- Export citation
FOUR-MANIFOLDS WITH POSITIVE CURVATURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 06 April 2020, pp. 245-257
- Print publication:
- May 2021
-
- Article
- Export citation
A support theorem for the X-ray transform on manifolds with plane covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 25 April 2019, pp. 149-158
- Print publication:
- July 2020
-
- Article
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
Statistics for Poisson Models of Overlapping Spheres
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 937-962
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Size distributions in random triangles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 283-295
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Universal Volume Comparison Theorem for Finsler Manifolds and Related Results
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1401-1435
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Estimation of the mean normal measure from flat sections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 31-48
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On Willmore's Inequality for Submanifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 474-480
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation