Refine search
Actions for selected content:
16 results
Perturbed cone theorems for proper harmonic maps
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal surfaces in the Lorentzian Heisenberg group
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 29 July 2025, pp. 579-608
- Print publication:
- November 2025
-
- Article
- Export citation
Biharmonic almost complex structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computing harmonic maps between Riemannian manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 531-580
- Print publication:
- April 2023
-
- Article
- Export citation
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 459-485
- Print publication:
- March 2022
-
- Article
- Export citation
ON HARMONIC AND PSEUDOHARMONIC MAPS FROM PSEUDO-HERMITIAN MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 06 November 2017, pp. 170-210
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
Heat Kernel Estimates Under the Ricci–Harmonic Map Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 22 February 2017, pp. 831-857
-
- Article
- Export citation
Les applications conforme-harmoniques
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-298
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation
Semi-invariant Submersions from Almost Hermitian Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-183
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
On Eells-Sampson’s existence theorem for harmonic maps via exponentially harmonic maps
-
- Journal:
- Nagoya Mathematical Journal / Volume 201 / March 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 133-146
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
SLANT CURVES IN CONTACT PSEUDO-HERMITIAN 3-MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 383-396
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
MINIMAL LAGRANGIAN 2-TORI IN $\mathbb{CP}^2$ COME IN REAL FAMILIES OF EVERY DIMENSION
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 29 March 2004, pp. 531-544
- Print publication:
- April 2004
-
- Article
- Export citation
Harmonic maps and cosymplectic manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 75-92
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
SPECIAL LAGRANGIAN CONES IN $\C^3$ AND PRIMITIVE HARMONIC MAPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 67 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 20 May 2003, pp. 769-789
- Print publication:
- June 2003
-
- Article
- Export citation
TODA EQUATIONS AND PLÜCKER FORMULAE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 145-151
- Print publication:
- March 2003
-
- Article
- Export citation
HARMONIC MORPHISMS AND SUBMANIFOLDS WITH CONFORMAL SECOND FUNDAMENTAL FORMS
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 01 May 2003, pp. 143-151
- Print publication:
- January 2003
-
- Article
-
- You have access
- Export citation




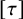
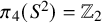
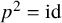
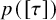
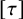
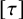
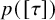
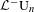
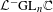
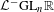
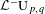
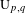
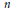
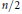
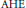
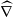 , we construct the parametric equations of Legendre pseudo-Hermitian circles (whose
, we construct the parametric equations of Legendre pseudo-Hermitian circles (whose  -geodesic curvature
-geodesic curvature 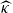 is constant and
is constant and 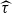 is zero) in
is zero) in 