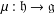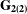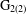Refine search
Actions for selected content:
4 results
On G2-manifolds and geometry in dimensions 6 and 8
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-9
-
- Article
- Export citation
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
ON COMPACT HOMOGENEOUS
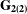 $\mathbf{\text{G}_{2(2)}}$-MANIFOLDS
$\mathbf{\text{G}_{2(2)}}$-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 71-80
- Print publication:
- February 2021
-
- Article
- Export citation
Deformations of G 2 and Spin(7) Structures
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 5 / 01 October 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1012-1055
- Print publication:
- 01 October 2005
-
- Article
-
- You have access
- Export citation