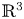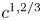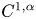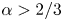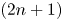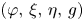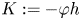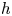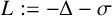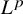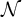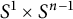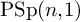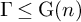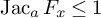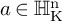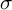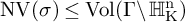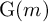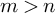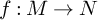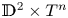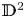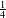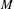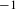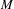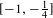Refine search
Actions for selected content:
25 results
Approximate control of the marked length spectrum by short geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 October 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Alexandrov sphere theorems for
 $ W^{2,n} $-hypersurfaces
$ W^{2,n} $-hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3698-3727
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The geometry of C1,α flat isometric immersions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conformally flat minimal Legendrian submanifolds in the unit sphere
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-30
-
- Article
- Export citation
FIRST EIGENVALUE CHARACTERISATION OF CLIFFORD HYPERSURFACES AND VERONESE SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 April 2024, pp. 164-173
- Print publication:
- February 2025
-
- Article
- Export citation
Stability of isometric immersions of hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rigidity result for the product of spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 574-581
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of capillary surfaces in compact 3-manifolds with strictly convex boundary
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 231-240
-
- Article
- Export citation
Homogeneous and curvature homogeneous Lorentzian critical metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1272-1296
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Carnot metrics, dynamics and local rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 614-664
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NATURAL MAPS FOR MEASURABLE COCYCLES OF COMPACT HYPERBOLIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 421-448
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discs area-minimizing in mean convex Riemannian n-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1361-1382
- Print publication:
- December 2022
-
- Article
- Export citation
ON ALMOST STABLE CMC HYPERSURFACES IN MANIFOLDS OF BOUNDED SECTIONAL CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 September 2019, pp. 333-338
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
COMPLETE WEINGARTEN HYPERSURFACES SATISFYING AN OKUMURA TYPE INEQUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 81-92
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Higher rank rigidity for Berwald spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 18 December 2018, pp. 1991-2016
- Print publication:
- July 2020
-
- Article
- Export citation
Hyperbolic rank rigidity for manifolds of
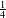 $\frac{1}{4}$-pinched negative curvature
$\frac{1}{4}$-pinched negative curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1194-1216
- Print publication:
- May 2020
-
- Article
- Export citation
The structure of the Ricci tensor on locally homogeneous Lorentzian gradient Ricci solitons
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 February 2018, pp. 461-482
- Print publication:
- June 2018
-
- Article
- Export citation
QUANTITATIVE OSCILLATION ESTIMATES FOR ALMOST-UMBILICAL CLOSED HYPERSURFACES IN EUCLIDEAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 17 April 2015, pp. 133-144
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Infinitesimal Rigidity of Convex Polyhedra through the Second Derivative of the Hilbert–Einstein Functional
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 783-825
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation