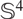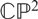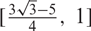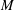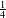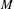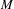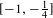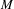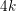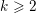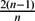Refine search
Actions for selected content:
54 results
COMPLETE HYPERSURFACES WITH LINEARLY RELATED HIGHER ORDER MEAN CURVATURES IN THE HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 82-105
- Print publication:
- August 2025
-
- Article
- Export citation
Free torus actions and twisted suspensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of generalized Yamabe solitons and its applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
- Export citation
A note on almost Yamabe solitons
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
- Print publication:
- January 2024
-
- Article
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
On complete submanifolds with parallel normalized mean curvature in product spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 331-355
- Print publication:
- April 2022
-
- Article
- Export citation
On pull-backs of the universal connection
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 845-859
- Print publication:
- December 2022
-
- Article
- Export citation
Carnot metrics, dynamics and local rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 614-664
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unique continuation properties for polyharmonic maps between Riemannian manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1-28
- Print publication:
- February 2023
-
- Article
- Export citation
A NOTE ON THE CLASSIFICATION OF NONCOMPACT QUASI-EINSTEIN MANIFOLDS WITH VANISHING CONDITION ON THE WEYL TENSOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 07 May 2021, pp. 336-346
- Print publication:
- May 2022
-
- Article
- Export citation
Sharp Caffarelli–Kohn–Nirenberg inequalities on Riemannian manifolds: the influence of curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 102-127
- Print publication:
- February 2022
-
- Article
- Export citation
Some results on Ricci-Bourguignon solitons and almost solitons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 591-604
- Print publication:
- September 2021
-
- Article
- Export citation
FOUR-MANIFOLDS WITH POSITIVE CURVATURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 06 April 2020, pp. 245-257
- Print publication:
- May 2021
-
- Article
- Export citation
Moduli Spaces of Metrics of Positive Scalar Curvature on Topological Spherical Space Forms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 901-908
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
Isospectrality for Orbifold Lens Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 281-325
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
Comparison Geometry of Manifolds with Boundary under a Lower Weighted Ricci Curvature Bound
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 October 2018, pp. 243-280
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Hyperbolic rank rigidity for manifolds of
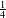 $\frac{1}{4}$-pinched negative curvature
$\frac{1}{4}$-pinched negative curvature
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1194-1216
- Print publication:
- May 2020
-
- Article
- Export citation
From ALE to ALF gravitational instantons
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 1159-1221
- Print publication:
- June 2018
-
- Article
- Export citation
VANISHING THEOREMS FOR HYPERSURFACES IN THE UNIT SPHERE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 661-671
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation