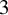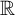Refine search
Actions for selected content:
21 results
Perturbed cone theorems for proper harmonic maps
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 October 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
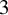 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foliated affine and projective structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1153-1187
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerically non-special varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1428-1447
- Print publication:
- June 2022
-
- Article
- Export citation
Characterization of totally geodesic foliations with integrable and parallelizable normal bundle
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 128-137
- Print publication:
- January 2023
-
- Article
- Export citation
LOSIK CLASSES FOR CODIMENSION-ONE FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1391-1419
- Print publication:
- July 2022
-
- Article
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
On Lorentzian surfaces in ℝ2,2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 61-88
- Print publication:
- February 2017
-
- Article
- Export citation
Left Invariant Einstein–Randers Metrics on Compact Lie Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 870-881
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
CONTACT METRIC (κ,μ)-SPACES AS BI-LEGENDRIAN MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 373-386
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON TRANSVERSALLY HARMONIC MAPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 1-16
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
A CLASSIFICATION OF HORIZONTALLY HOMOTHETIC SUBMERSIONS FROM SPACE FORMS OF NONNEGATIVE CURVATURE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 31 May 2006, pp. 485-493
- Print publication:
- June 2006
-
- Article
- Export citation
RESIDUES OF HOLOMORPHIC FOLIATIONS RELATIVE TO A GENERAL SUBMANIFOLD
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 01 June 2005, pp. 435-445
- Print publication:
- June 2005
-
- Article
- Export citation
An Integral Formula on Seifert Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-357
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FOLIATIONS, HARMONIC MORPHISMS AND THE WALCZAK FORMULA
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 17 November 2003, pp. 781-794
- Print publication:
- December 2003
-
- Article
- Export citation
HARMONIC MORPHISMS AND SUBMANIFOLDS WITH CONFORMAL SECOND FUNDAMENTAL FORMS
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 01 May 2003, pp. 143-151
- Print publication:
- January 2003
-
- Article
-
- You have access
- Export citation
The Local Möbius Equation and Decomposition Theorems in Riemannian Geometry
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 3 / 01 September 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-387
- Print publication:
- 01 September 2002
-
- Article
-
- You have access
- Export citation
Linéarisation symplectique en dimension 2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 2 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-139
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation
Invariant submanifolds in flow geometry
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-314
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Mean Curvature of Riemannian Foliations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 1 / 01 March 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-105
- Print publication:
- 01 March 1996
-
- Article
-
- You have access
- Export citation