Refine search
Actions for selected content:
17 results
Asymptotic behaviour of large-scale solutions of Hitchin’s equations in higher rank
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic and analytic compactifications of the Hitchin moduli space
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bismut Ricci flat manifolds with symmetries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 26 July 2022, pp. 1371-1390
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 778-803
- Print publication:
- June 2023
-
- Article
- Export citation
Moduli of wild Higgs bundles on
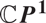 $\mathbb{C}P^1$ with
$\mathbb{C}P^1$ with 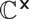 $\mathbb{C}^\times$-actions
$\mathbb{C}^\times$-actions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 03 June 2021, pp. 623-656
- Print publication:
- November 2021
-
- Article
- Export citation
On certain Tannakian categories of integrable connections over Kähler manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1034-1061
- Print publication:
- August 2022
-
- Article
- Export citation
Singular G-Monopoles on S 1 × Σ
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 5 / 01 October 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1096-1119
- Print publication:
- 01 October 2016
-
- Article
-
- You have access
- Export citation
Polystable Parabolic Principal G-Bundles and Hermitian-Einstein Connections
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-54
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
Coupled Vortex Equations on Complete Kähler Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 3 / 01 September 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-480
- Print publication:
- 01 September 2008
-
- Article
-
- You have access
- Export citation
Gluing an Infinite Number of Instantons
-
- Journal:
- Nagoya Mathematical Journal / Volume 188 / December 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 107-131
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Hermitian Harmonic Maps into Convex Balls
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 1 / 01 March 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-122
- Print publication:
- 01 March 2007
-
- Article
-
- You have access
- Export citation
Twisted complex geometry
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-296
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Connections on a Parabolic Principal Bundle Over a Curve
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 2 / 01 April 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 262-281
- Print publication:
- 01 April 2006
-
- Article
-
- You have access
- Export citation
Hermitian Yang–Mills–Higgs Metrics on Complete Kähler Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 4 / 01 August 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 871-896
- Print publication:
- 01 August 2005
-
- Article
-
- You have access
- Export citation
L2 Extension for jets of holomorphic sections of a Hermitian line Bundle
-
- Journal:
- Nagoya Mathematical Journal / Volume 180 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-34
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
Wild non-abelian Hodge theory on curves
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 179-204
- Print publication:
- January 2004
-
- Article
-
- You have access
- Export citation
Configurations de Particules et Espaces de Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 1 / 01 March 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 66-79
- Print publication:
- 01 March 1995
-
- Article
-
- You have access
- Export citation
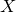
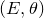
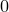
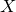
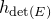
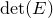
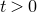
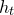
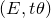
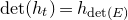
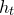
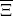
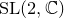
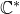

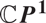
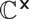
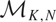
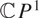
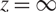
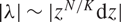
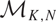
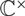
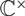
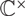
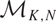
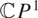
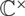
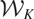
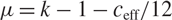
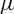
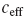
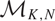
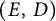
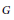
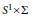
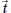
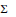
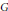
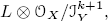 which satisfies a certain L
which satisfies a certain L