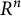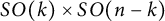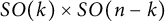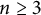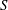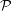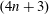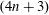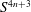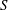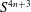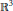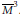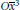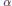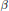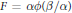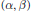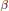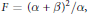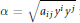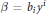Refine search
Actions for selected content:
23 results
Sharp Hardy and spectral gap inequalities on special irreversible Finsler manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-36
-
- Article
- Export citation
On Riemannian and Ricci curvatures of homogeneous Finsler manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 73-90
- Print publication:
- March 2025
-
- Article
- Export citation
On the Pontrjagin classes of spray manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 544-553
- Print publication:
- September 2024
-
- Article
- Export citation
Proof of Laugwitz Conjecture and Landsberg Unicorn Conjecture for Minkowski norms with
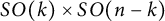 $SO(k)\times SO(n-k)$-symmetry
$SO(k)\times SO(n-k)$-symmetry
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 1486-1516
- Print publication:
- October 2022
-
- Article
- Export citation
DEFORMATIONS OF THE VERONESE EMBEDDING AND FINSLER
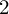 $2$-SPHERES OF CONSTANT CURVATURE
$2$-SPHERES OF CONSTANT CURVATURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 2103-2134
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Metrizability of Holonomy Invariant Projective Deformation of Sprays
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 January 2020, pp. 701-714
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE PROBLEM OF NON-BERWALDIAN LANDSBERG SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 331-341
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Homogeneous Einstein Finsler Metrics on
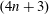 $(4n+3)$-dimensional Spheres
$(4n+3)$-dimensional Spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 November 2018, pp. 509-523
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Ricci Curvature Tensor and Non-Riemannian Quantities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 3 / 01 September 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 530-537
- Print publication:
- 01 September 2015
-
- Article
-
- You have access
- Export citation
Helicoidal Minimal Surfaces in a Finsler Space of Randers Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 765-779
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Erratum to the Paper “A Lower Bound for the Length of Closed Geodesics on a Finsler Manifold”
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, p. 209
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Length of Closed Geodesics on a Finsler Manifold
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 194-208
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
A Universal Volume Comparison Theorem for Finsler Manifolds and Related Results
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1401-1435
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Randers Metrics of Constant Scalar Curvature
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 615-620
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
On Some Non-Riemannian Quantities in Finsler Geometry
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-193
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
A Note on Randers Metrics of Scalar Flag Curvature
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 474-486
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
Projectively Flat Fourth Root Finsler Metrics
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 138-145
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
On a Class of Landsberg Metrics in Finsler Geometry
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1357-1374
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
On Projectively Flat (α, β)-metrics
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 132-144
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
On a Class of Projectively Flat Metrics with Constant Flag Curvature
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 2 / 01 April 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 443-456
- Print publication:
- 01 April 2008
-
- Article
-
- You have access
- Export citation