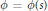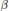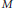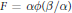Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tayebi, A.
and
Peyghan, E.
2010.
On Ricci tensors of Randers metrics.
Journal of Geometry and Physics,
Vol. 60,
Issue. 11,
p.
1665.
Hushmandi, Ataabak B.
and
Rezaii, Morteza M.
2011.
On warped product Finsler spaces of Landsberg type.
Journal of Mathematical Physics,
Vol. 52,
Issue. 9,
YANG, GUOJUN
2013.
ON A CLASS OF SINGULAR PROJECTIVELY FLAT FINSLER METRICS WITH CONSTANT FLAG CURVATURE.
International Journal of Mathematics,
Vol. 24,
Issue. 10,
p.
1350087.
Yang, Guojun
Mira, P.
and
Mokhov, O.
2013.
On a Class of Two‐Dimensional Douglas and Projectively Flat Finsler Metrics.
The Scientific World Journal,
Vol. 2013,
Issue. 1,
Yang, Guo Jun
2013.
On a class of two-dimensional projectively flat finsler metrics with constant flag curvature.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 5,
p.
959.
Zou, Yangyang
and
Cheng, Xinyue
2014.
The generalized unicorn problem on(α,β)-metrics.
Journal of Mathematical Analysis and Applications,
Vol. 414,
Issue. 2,
p.
574.
Yang, Guojun
2014.
On a class of singular Douglas and projectively flat Finsler metrics.
Differential Geometry and its Applications,
Vol. 32,
Issue. ,
p.
113.
Zhou, Linfeng
2014.
The Finsler surface withK=0andJ=0.
Differential Geometry and its Applications,
Vol. 35,
Issue. ,
p.
370.
Chen, Guangzu
He, Qun
and
Pan, Shengliang
2014.
On weak Berwald(α,β)-metrics of scalar flag curvature.
Journal of Geometry and Physics,
Vol. 86,
Issue. ,
p.
112.
Tayebi, Akbar
and
Sadeghi, Hassan
2015.
On generalized Douglas–Weyl (α, β)-metrics.
Acta Mathematica Sinica, English Series,
Vol. 31,
Issue. 10,
p.
1611.
Yu, Changtao
2015.
On dually flat general (α,β)-metrics.
Differential Geometry and its Applications,
Vol. 40,
Issue. ,
p.
111.
Huang, Libing
2015.
On the fundamental equations of homogeneous Finsler spaces.
Differential Geometry and its Applications,
Vol. 40,
Issue. ,
p.
187.
HE, Yong
and
ZHONG, Chunping
2016.
On doubly warped product of complex finsler manifolds.
Acta Mathematica Scientia,
Vol. 36,
Issue. 6,
p.
1747.
Liu, Wangfu
and
Li, Benling
2016.
Projectively flat Finsler metrics defined by the Euclidean metric and related 1-forms.
Differential Geometry and its Applications,
Vol. 46,
Issue. ,
p.
14.
Zohrehvand, M.
and
Maleki, H.
2016.
On general (α,β)-metrics of Landsberg type.
International Journal of Geometric Methods in Modern Physics,
Vol. 13,
Issue. 06,
p.
1650085.
Zhao, Wei
and
Shen, Yibing
2016.
A Cheeger finiteness theorem for Finsler manifolds.
Journal of Mathematical Analysis and Applications,
Vol. 433,
Issue. 2,
p.
1690.
Deng, Shaoqiang
and
Xu, Ming
2016.
$$(\alpha _1,\alpha _2)$$ ( α 1 , α 2 ) -Metrics and Clifford–Wolf Homogeneity.
The Journal of Geometric Analysis,
Vol. 26,
Issue. 3,
p.
2282.
Pişcoran, Laurian-Ioan
and
Mishra, Vishnu Narayan
2017.
S-curvature for a new class of $$(\alpha , \beta )$$ ( α , β ) -metrics.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 111,
Issue. 4,
p.
1187.
TAYEBI, AKBAR
Nankali, Ali
and
Najafi, Behzad
2018.
On the Class of Einstein Exponential-Type Finsler Metrics.
Zurnal matematiceskoj fiziki, analiza, geometrii,
Vol. 14,
Issue. 1,
p.
100.
He, Yong
and
Zhong, Chunping
2018.
Strongly convex weakly complex Berwald metrics and real Landsberg metrics.
Science China Mathematics,
Vol. 61,
Issue. 3,
p.
535.