Refine search
Actions for selected content:
15 results
Conformally Kähler structures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
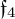 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 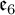 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 01 March 2024, pp. 940-974
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective invariants of images
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 936-946
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
DUALITY OF (2, 3, 5)-DISTRIBUTIONS AND LAGRANGIAN CONE STRUCTURES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 23 January 2020, pp. 303-315
- Print publication:
- September 2021
-
- Article
- Export citation
Equi-affine differential invariants for invariant feature point detection
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 06 March 2019, pp. 277-296
-
- Article
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
On Lorentzian surfaces in ℝ2,2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 61-88
- Print publication:
- February 2017
-
- Article
- Export citation
Geometric Invariants of Cuspidal Edges
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-462
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
ON THE GEOMETRY OF THE SPACE OF ORIENTED LINES OF THE HYPERBOLIC SPACE
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 2 / May 2007
- Published online by Cambridge University Press:
- 09 August 2007, pp. 357-366
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
Two Algorithms for a Moving Frame Construction
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 2 / 01 April 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-291
- Print publication:
- 01 April 2003
-
- Article
-
- You have access
- Export citation
Invariant theory for linear differential systems modeled after the grassmannian Gr(n, 2n)
-
- Journal:
- Nagoya Mathematical Journal / Volume 171 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 163-186
- Print publication:
- 2003
-
- Article
-
- You have access
- Export citation
On Strongly Convex Indicatrices in Minkowski Geometry
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 2 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 232-246
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation












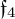
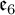













 of the “complexified unit circle”
of the “complexified unit circle” 


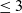
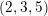
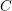
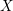
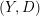
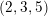
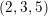
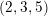
 of oriented geodesics of
of oriented geodesics of 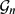 and
and 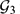 is Kähler and find an orthogonal almost complex structure on
is Kähler and find an orthogonal almost complex structure on 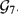 .
.