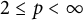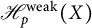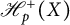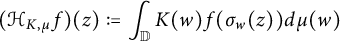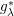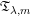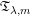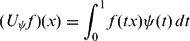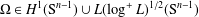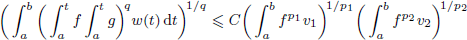Refine search
Actions for selected content:
28 results
Sobolev regularity of the Bergman projection on a class of singular Reinhardt domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-17
-
- Article
- Export citation
Volterra operators between Hardy spaces of vector-valued Dirichlet series
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 286-300
- Print publication:
- March 2025
-
- Article
- Export citation
A class of Hausdorff–Berezin operators on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1069-1080
- Print publication:
- December 2024
-
- Article
- Export citation
Hausdorff operators on some classical spaces of analytic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 768-780
- Print publication:
- September 2024
-
- Article
- Export citation
On Hardy kernels as reproducing kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 428-442
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp Bounds for Oscillatory Integral Operators with Homogeneous Polynomial Phases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 771-786
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH
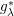 $g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 28 August 2018, pp. 123-152
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 28 January 2018, pp. 13-24
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
The Gradient of a Solution of the Poisson Equation in the Unit Ball and Related Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 536-545
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
A NOTE ON MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES OF REVOLUTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 380-402
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Iterating Bilinear Hardy Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 955-971
-
- Article
- Export citation
Linear non-local diffusion problems in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 833-863
- Print publication:
- August 2016
-
- Article
- Export citation
Measures of Noncompactness in Regular Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 780-793
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
New Characterizations of the Weighted Composition Operators Between Bloch Type Spaces in the Polydisk
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-802
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
On the p-norm of an Integral Operator in the Half Plane
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 593-601
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
MIXED NORM INEQUALITIES FOR SOME DIRECTIONAL MAXIMAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 448-455
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS IN NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 324-334
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
SELFADJOINTNESS OF INTEGRAL AND MATRIX OPERATORS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 762-782
- Print publication:
- June 2006
-
- Article
- Export citation
SMALL DEVIATIONS OF RIEMANN--LIOUVILLE PROCESSES IN ${L_{\lowercase{q}}}$ SPACES WITH RESPECT TO FRACTAL MEASURES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 19 December 2005, pp. 224-250
- Print publication:
- January 2006
-
- Article
- Export citation