Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-10T22:37:07.502Z Has data issue: false hasContentIssue false
  • English
  • Français

Volterra operators between Hardy spaces of vector-valued Dirichlet series

Part of: Linear function spaces and their duals Series expansions Harmonic analysis in several variables Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  09 January 2025

Jiale Chen Open the ORCID record for Jiale Chen [Opens in a new window]
Jiale Chen*
Affiliation:
School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, China
*
e-mail: jialechen@snnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 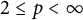$2\leq p<\infty $ and X be a complex infinite-dimensional Banach space. It is proved that if X is p-uniformly PL-convex, then there is no nontrivial bounded Volterra operator from the weak Hardy space 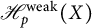$\mathscr {H}^{\text {weak}}_p(X)$ to the Hardy space 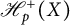$\mathscr {H}^+_p(X)$ of vector-valued Dirichlet series. To obtain this, a Littlewood–Paley inequality for Dirichlet series is established.

Keywords

Volterra operatorvector-valued Dirichlet seriesHardy spaceLittlewood–Paley inequality

MSC classification

Primary: 47G10: Integral operators 30B50: Dirichlet series and other series expansions, exponential series 42B30: $H^p$-spaces
Secondary: 46E40: Spaces of vector- and operator-valued functions
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Fundamental Research Funds for the Central Universities (Grant No. GK202207018) of China.

References

Avetisyan, K., Djordjević, O. and Pavlović, M., Littlewood–Paley inequalities in uniformly convex and uniformly smooth Banach spaces . J. Math. Anal. Appl. 336(2007), no. 1, 31–43.CrossRefGoogle Scholar
Bayart, F., Hardy spaces of Dirichlet series and their composition operators . Monatsh. Math. 136(2002), no. 3, 203–236.CrossRefGoogle Scholar
Bayart, F., Opérateurs de composition sur des espaces de séries de Dirichlet et problèmes d’hypercyclicité simultanés, Thèse à l’Université des Sciences et Technologies de Lille, 2002.Google Scholar
Blasco, O. and Pavlović, M., Complex convexity and vector-valued Littlewood–Paley inequalities . Bull. London Math. Soc. 35(2003), no. 6, 749–758.CrossRefGoogle Scholar
Bonet, J., Abscissas of weak convergence of vector valued Dirichlet series . J. Funct. Anal. 269(2015), no. 12, 3914–3927.CrossRefGoogle Scholar
Brevig, O. F., Perfekt, K.-M. and Seip, K., Volterra operators on Hardy spaces of Dirichlet series . J. Reine Angew. Math. 754(2019), 179–223.CrossRefGoogle Scholar
Carando, D., Defant, A. and Sevilla-Peris, P., Bohr’s absolute convergence problem for $\mathscr{H}_p$ -Dirichlet series in Banach spaces . Anal. PDE 7(2014), no. 2, 513–527.CrossRefGoogle Scholar
Carando, D., Defant, A. and Sevilla-Peris, P., Almost sure-sign convergence of Hardy-type Dirichlet series . J. Anal. Math. 135(2018), no. 1, 225–247.CrossRefGoogle Scholar
Carando, D., Marceca, F. and Sevilla-Peris, P., Hausdorff–Young-type inequalities for vector-valued Dirichlet series . Trans. Amer. Math. Soc. 373(2020), no. 8, 5627–5652.CrossRefGoogle Scholar
Carando, D., Marceca, F., Scotti, M. and Tradacete, P., Random unconditional convergence of vector-valued Dirichlet series . J. Funct. Anal. 277(2019), no. 9, 3156–3178.CrossRefGoogle Scholar
Chen, J. and Wang, M., Generalized integration operators from weak to strong spaces of vector-valued analytic functions . Taiwanese J. Math. 25(2021), no. 4, 757–774.CrossRefGoogle Scholar
Davis, W. J., Garling, D. J. H. and Tomczak-Jaegermann, N., The complex convexity of quasi-normed linear spaces . J. Funct. Anal. 55(1984), no. 1, 110–150.CrossRefGoogle Scholar
Defant, A., García, D., Maestre, M. and Pérez-García, D., Bohr’s strip for vector valued Dirichlet series . Math. Ann. 342(2008), no. 3, 533–555.CrossRefGoogle Scholar
Defant, A., García, D., Maestre, M. and Sevilla-Peris, P., Dirichlet series and holomorphic functions in high dimensions, Cambridge University Press, Cambridge, 2019.CrossRefGoogle Scholar
Defant, A. and Pérez, A., Hardy spaces of vector-valued Dirichlet series . Studia Math. 243(2018), no. 1, 53–78.CrossRefGoogle Scholar
Defant, A., Pérez, A. and Sevilla-Peris, P., A note on abscissas of Dirichlet series . Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM. 113(2019), no. 3, 2639–2653.CrossRefGoogle Scholar
Defant, A., Schwarting, U. and Sevilla-Peris, P., Estimates for vector valued Dirichlet polynomials . Monatsh. Math. 175(2014), no. 1, 89–116.CrossRefGoogle Scholar
Diestel, J., Jarchow, H. and Tonge, A., Absolutely summing operators, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Freniche, F. J., García-Vázquez, J. C. and Rodríguez-Piazza, L., Operators into Hardy spaces and analytic Pettis integrable functions, Recent progress in functional analysis (Valencia, 2000). North-Holland Math. Stud. 189(2001), pp. 349–362.Google Scholar
Hedenmalm, H., Lindqvist, P. and Seip, K., A Hilbert space of Dirichlet series and systems of dilated functions in ${L}^2(0,1)$ . Duke Math. J. 86(1997), no. 1, 1–37.CrossRefGoogle Scholar
Jevtić, M., Vukotić, D. and Arsenović, M., Taylor coefficients and coefficient multipliers of Hardy and Bergman-type spaces, Springer International Publishing, Cham, 2016.CrossRefGoogle Scholar
Laitila, J., Weakly compact composition operators on vector-valued BMOA. J. Math. Anal. Appl. 308(2005), no. 2, 730–745.CrossRefGoogle Scholar
Laitila, J. and Tylli, H.-O., Composition operators on vector-valued harmonic functions and Cauchy transforms . Indiana Univ. Math. J. 55(2006), no. 2, 719–746.CrossRefGoogle Scholar
Laitila, J., Tylli, H.-O. and Wang, M., Composition operators from weak to strong spaces of vector-valued analytic functions . J. Operator Theory 62(2009), no. 2, 281–295.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. II, Springer-Verlag, Berlin-New York, 1979.CrossRefGoogle Scholar
Littlewood, J. E. and Paley, R. E. A. C., Theorems on Fourier series and power series (II) . Proc. London Math. Soc. (2) 42(1936), no. 1, 52–89.Google Scholar
Pommerenke, Ch., Schlichte Funktionen und analytische Funktionen von beschränkter mittlerer Oszillation . Comment. Math. Helv. 52(1977), no. 4, 591–602.CrossRefGoogle Scholar
Queffélec, H. and Queffélec, M., Diophantine approximation and Dirichlet series, Second edition, Springer, Singapore, 2020.CrossRefGoogle Scholar
Weissler, F. B., Logarithmic Sobolev inequalities and hypercontractive estimates on the circle . J. Funct. Anal. 37(1980), no. 2, 218–234.CrossRefGoogle Scholar