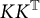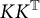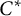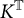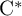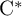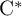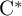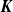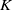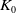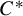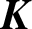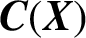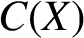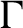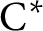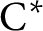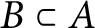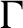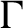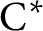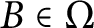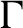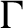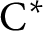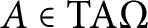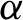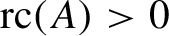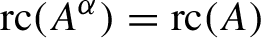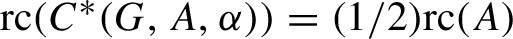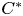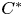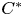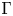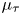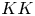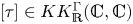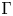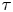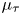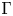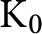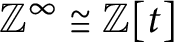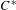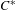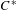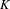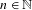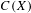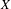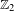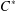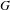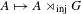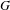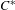Refine search
Actions for selected content:
89 results
Ideal structure of uniform Roe algebras: beyond Property A
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLE TRACIALLY
 $\mathcal {Z}$-ABSORBING C*-ALGEBRAS
$\mathcal {Z}$-ABSORBING C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 2135-2179
- Print publication:
- November 2025
-
- Article
- Export citation
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
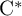 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE EVANS CHAIN COMPLEX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 552-562
- Print publication:
- June 2025
-
- Article
- Export citation
Goldie dimension for C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 200-223
-
- Article
- Export citation
Unitary groups,
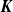 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 229-251
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Binary factors of shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 888-932
- Print publication:
- March 2024
-
- Article
- Export citation
RATIONAL
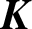 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 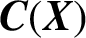 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 119-144
- Print publication:
- August 2023
-
- Article
- Export citation
A counterexample to the HK-conjecture that is principal
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1829-1846
- Print publication:
- June 2023
-
- Article
- Export citation
Uniform property
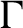 $\Gamma $ for certain
$\Gamma $ for certain 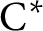 $\mathrm {C^*}$-algebras
$\mathrm {C^*}$-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1063-1070
- Print publication:
- December 2022
-
- Article
- Export citation
C*-algebras where every element is a limit of products of positive elements
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 628-632
- Print publication:
- September 2022
-
- Article
- Export citation
The Cuntz semigroup and the radius of comparison of the crossed product by a finite group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 10 March 2021, pp. 3541-3592
- Print publication:
- December 2021
-
- Article
- Export citation
Classification of irreversible and reversible Pimsner operator algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 13 January 2021, pp. 2510-2535
- Print publication:
- December 2020
-
- Article
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation
Dimension groups for self-similar maps and matrix representations of the cores of the associated C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 1013-1056
- Print publication:
- August 2021
-
- Article
- Export citation
Rokhlin dimension: duality, tracial properties, and crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 408-460
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
HOMOLOGY AND MATUI’S HK CONJECTURE FOR GROUPOIDS ON ONE-DIMENSIONAL SOLENOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 105-117
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
The maximal injective crossed product
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 22 April 2019, pp. 2995-3014
- Print publication:
- November 2020
-
- Article
-
- You have access
- Open access
- Export citation