Article contents
The stable algebra of a Wieler solenoid: inductive limits and 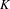 $K$ -theory
$K$ -theory
Published online by Cambridge University Press: 10 April 2019
Abstract
Wieler has shown that every irreducible Smale space with totally disconnected stable sets is a solenoid (i.e., obtained via a stationary inverse limit construction). Using her construction, we show that the associated stable 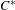 $C^{\ast }$ -algebra is the stationary inductive limit of a
$C^{\ast }$ -algebra is the stationary inductive limit of a 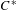 $C^{\ast }$ -stable Fell algebra that has a compact spectrum and trivial Dixmier–Douady invariant. This result applies in particular to Williams solenoids along with other examples. Beyond the structural implications of this inductive limit, one can use this result to, in principle, compute the
$C^{\ast }$ -stable Fell algebra that has a compact spectrum and trivial Dixmier–Douady invariant. This result applies in particular to Williams solenoids along with other examples. Beyond the structural implications of this inductive limit, one can use this result to, in principle, compute the 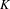 $K$ -theory of the stable
$K$ -theory of the stable 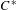 $C^{\ast }$ -algebra. A specific one-dimensional Smale space (the
$C^{\ast }$ -algebra. A specific one-dimensional Smale space (the 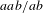 $aab/ab$ -solenoid) is considered as an illustrative running example throughout.
$aab/ab$ -solenoid) is considered as an illustrative running example throughout.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 6
- Cited by


