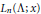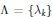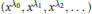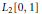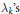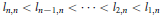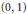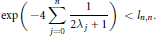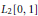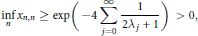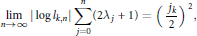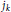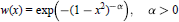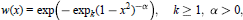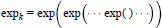Refine search
Actions for selected content:
8 results
Christoffel Functions and Universality in the Bulk for Multivariate Orthogonal Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 3 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 600-620
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
On the Smallest and Largest Zeros of Müntz-Legendre Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 194-202
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
Matrix Valued Orthogonal Polynomials on the Unit Circle: Some Extensions of the Classical Theory
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-104
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
Extrapolation of the functional calculus of generalized Dirac operators and related embedding and Littlewood-Paley-type theorems. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-326
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Operator-valued multiplier theorems characterizing Hilbert spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-184
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Mean Convergence of Lagrange Interpolation for Exponential weights on [-1, 1]
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 6 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1273-1297
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation
Homogeneous solutions of the generalized heat equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-45
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
The Appell transform and the semigroup property for temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-117
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation