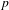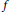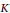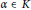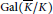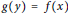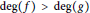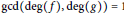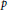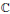Given two monic polynomials 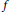 $f$ and
$f$ and  $g$ with coefficients in a number field
$g$ with coefficients in a number field 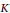 $K$ , and some
$K$ , and some 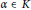 $\alpha \,\in \,K$ , we examine the action of the absolute Galois group
$\alpha \,\in \,K$ , we examine the action of the absolute Galois group 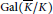 $Gal\left( \bar{K}/K \right)$ on the directed graph of iterated preimages of
$Gal\left( \bar{K}/K \right)$ on the directed graph of iterated preimages of  $\alpha $ under the correspondence
$\alpha $ under the correspondence 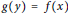 $g\left( y \right)\,=\,f\left( x \right)$ , assuming that
$g\left( y \right)\,=\,f\left( x \right)$ , assuming that 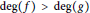 $\deg \left( f \right)\,>\,\deg \left( g \right)$ and that
$\deg \left( f \right)\,>\,\deg \left( g \right)$ and that 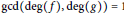 $\gcd \left( \deg \left( f \right),\deg \left( g \right) \right)\,=1$ . If a prime of
$\gcd \left( \deg \left( f \right),\deg \left( g \right) \right)\,=1$ . If a prime of 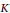 $K$ exists at which
$K$ exists at which 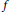 $f$ and
$f$ and  $g$ have integral coefficients and at which
$g$ have integral coefficients and at which  $\alpha $ is not integral, we show that this directed graph of preimages consists of finitely many
$\alpha $ is not integral, we show that this directed graph of preimages consists of finitely many 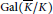 $Gal\left( \bar{K}/K \right)$ -orbits. We obtain this result by establishing a
$Gal\left( \bar{K}/K \right)$ -orbits. We obtain this result by establishing a 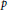 $p$ -adic uniformization of such correspondences, tenuously related to Böttcher’s uniformization of polynomial dynamical systems over
$p$ -adic uniformization of such correspondences, tenuously related to Böttcher’s uniformization of polynomial dynamical systems over 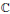 $\mathbb{C}$ , although the construction of a Böttcher coordinate for complex holomorphic correspondences remains unresolved.
$\mathbb{C}$ , although the construction of a Böttcher coordinate for complex holomorphic correspondences remains unresolved.
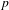 $p$ -adic plane automorphisms
$p$ -adic plane automorphisms