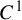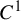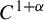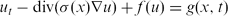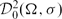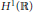Refine search
Actions for selected content:
12 results
Pullback measure attractors for stochastic p-Laplacian parabolic equations on thin domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 August 2025, pp. 1-28
-
- Article
- Export citation
Pullback measure attractors for non-autonomous stochastic lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-20
-
- Article
- Export citation
Measures of maximal and full dimension for smooth maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 31-49
- Print publication:
- January 2024
-
- Article
- Export citation
LYAPUNOV EXPONENTS OF THE KURAMOTO–SIVASHINSKY PDE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 15 July 2019, pp. 270-285
-
- Article
-
- You have access
- Export citation
Time-dependent attractors for non-autonomous non-local reaction–diffusion equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 957-981
- Print publication:
- October 2018
-
- Article
- Export citation
REGULARITY AND FRACTAL DIMENSION OF PULLBACK ATTRACTORS FOR A NON-AUTONOMOUS SEMILINEAR DEGENERATE PARABOLIC EQUATION
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 431-448
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
The Pullback Asymptotic Behavior of the Solutions for 2D Nonautonomous G-Navier-Stokes Equations
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 223-237
- Print publication:
- April 2012
-
- Article
- Export citation
The Global Attractor of a Damped, Forced Hirota Equation in H 1
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 2 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 295-310
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation
AMBIGUITY IN THE DETERMINATION OF THE FREE ENERGY ASSOCIATED WITH THE CRITICAL CIRCLE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 177-184
-
- Article
-
- You have access
- Export citation
DIMENSION ESTIMATE OF THE EXPONENTIAL ATTRACTOR FOR THE CHEMOTAXIS–GROWTH SYSTEM*
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 483-497
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
SPATIALLY NONDECAYING SOLUTIONS OF THE 2D NAVIER-STOKES EQUATION IN A STRIP
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 September 2007, pp. 525-588
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
EQUI-ATTRACTION AND THE CONTINUOUS DEPENDENCE OF ATTRACTORS ON PARAMETERS
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 January 2004, pp. 131-141
- Print publication:
- January 2004
-
- Article
-
- You have access
- Export citation