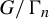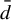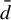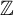Refine search
Actions for selected content:
82 results
Variational principles of metric mean dimension for random dynamical systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 September 2025, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
Sub-additivity of measure theoretic entropies of commuting transformations on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 10 July 2025, pp. 3430-3464
- Print publication:
- November 2025
-
- Article
- Export citation
Mean topological dimension of a random dynamical system for amenable groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1297-1328
-
- Article
- Export citation
ALGEBRAIC DYNAMICAL SYSTEMS FROM LDPC CODES SATISFY A STRONG NEGATION OF THE WEAK PINSKER PROPERTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 2317-2385
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modulus of continuity of invariant densities and entropies for piecewise expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 2976-2991
- Print publication:
- October 2025
-
- Article
- Export citation
RELATIVE POSITION BETWEEN A PAIR OF SPIN MODEL SUBFACTORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
- Print publication:
- August 2025
-
- Article
- Export citation
Some remarks about self-products and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2183-2193
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rank-one systems, flexible classes and Shannon orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2132-2182
- Print publication:
- July 2025
-
- Article
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the isomorphism problem between multidimensional substitutive subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2054-2094
- Print publication:
- July 2025
-
- Article
- Export citation
Rigidity of Lyapunov exponents for derived from Anosov diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 1444-1460
- Print publication:
- May 2025
-
- Article
- Export citation
Rank-one non-singular actions of countable groups and their odometer factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1078-1128
- Print publication:
- April 2025
-
- Article
- Export citation
Minimal and proximal examples of
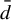 $\bar {d}$-stable and
$\bar {d}$-stable and 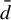 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 396-426
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A variational principle of amenable random metric mean dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 852-875
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
Non-existence of a universal zero-entropy system via generic actions of almost complete growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 3630-3644
- Print publication:
- December 2024
-
- Article
- Export citation
Entropy, virtual Abelianness and Shannon orbit equivalence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 3481-3500
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
- Export citation
Measures of maximal entropy of bounded density shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 20 February 2024, pp. 2960-2974
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation







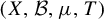
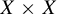
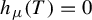
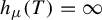
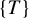
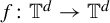
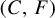
 of cofinite subgroups in
of cofinite subgroups in