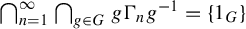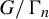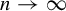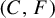1. Introduction
This work is motivated by a recent paper [Reference Foreman, Gao, Hill, Silva and WeissFo–We], where Foreman et al describe odometer factors of rank-one transformations in terms of the underlying cutting-and-stacking parameters. This description is considered as a step towards classification of the rank-one transformations up to isomorphism relation. Our purpose here is to generalize the main results of [Reference Foreman, Gao, Hill, Silva and WeissFo–We] in the following three directions:
-
• to consider actions of arbitrary countable infinite groups including non-amenable ones ([Reference Foreman, Gao, Hill, Silva and WeissFo–We] deals only with
 ${\mathbb Z}$
-actions);
${\mathbb Z}$
-actions); -
• to consider arbitrary non-singular group actions ([Reference Foreman, Gao, Hill, Silva and WeissFo–We] deals only with probability preserving actions); and
-
• to consider rank-one actions along an arbitrary sequence of shapes ([Reference Foreman, Gao, Hill, Silva and WeissFo–We] deals only with the classical rank one, that is, rank one along a sequence of intervals in
 ${\mathbb Z}$
. In particular, our results hold for the funny rank-one probability preserving
${\mathbb Z}$
. In particular, our results hold for the funny rank-one probability preserving
 ${\mathbb Z}$
-actions which were not studied in [Reference Foreman, Gao, Hill, Silva and WeissFo–We]).
${\mathbb Z}$
-actions which were not studied in [Reference Foreman, Gao, Hill, Silva and WeissFo–We]).
We now briefly outline the content of the paper, which consists of six sections. Section 2 is divided into seven subsections. In §2.1, we define, for an arbitrary countable group G, non-singular G-actions of rank one. According to this definition, a non-singular G-action T is of rank one if T is free and T admits a refining sequence of Rokhlin towers that approximate both the entire
![]() $\sigma $
-algebra of Borel subsets and the G-orbits and, in addition, the Radon–Nikodym derivative of T is constant on each transposition of the levels within every tower (see Definition 2.1). This extends the concept given in [Reference Rudolph and SilvaRuSi] for
$\sigma $
-algebra of Borel subsets and the G-orbits and, in addition, the Radon–Nikodym derivative of T is constant on each transposition of the levels within every tower (see Definition 2.1). This extends the concept given in [Reference Rudolph and SilvaRuSi] for
![]() ${\mathbb Z}$
-actions. Definition 2.1 can be considered as an abstract definition of rank one. In the case of probability preserving
${\mathbb Z}$
-actions. Definition 2.1 can be considered as an abstract definition of rank one. In the case of probability preserving
![]() ${\mathbb Z}$
-actions, there exist several equivalent constructive definitions of this concept [Reference FerencziFe]. One of the most useful of these is the cutting-and-stacking construction, which explicitly associates a rank-one transformation to a sequence of integer-valued parameters. (Thus, the class of rank-one transformations is parametrized with a nice Polish space of integer parameters. However, different sequences of parameters can define isomorphic rank-one maps. A challenging open problem in this field is to find necessary and sufficient conditions for the parameters that determine isomorphic transformations.) This transformation is defined on the unit interval. It preserves the Lebesgue measure. A natural generalization of this construction for general countable groups was suggested in [Reference DanilenkoDa1, Reference del JuncodJ2] in similar but non-equivalent versions. We call it the
${\mathbb Z}$
-actions, there exist several equivalent constructive definitions of this concept [Reference FerencziFe]. One of the most useful of these is the cutting-and-stacking construction, which explicitly associates a rank-one transformation to a sequence of integer-valued parameters. (Thus, the class of rank-one transformations is parametrized with a nice Polish space of integer parameters. However, different sequences of parameters can define isomorphic rank-one maps. A challenging open problem in this field is to find necessary and sufficient conditions for the parameters that determine isomorphic transformations.) This transformation is defined on the unit interval. It preserves the Lebesgue measure. A natural generalization of this construction for general countable groups was suggested in [Reference DanilenkoDa1, Reference del JuncodJ2] in similar but non-equivalent versions. We call it the
![]() $(C,F)$
-construction. The most general version of the
$(C,F)$
-construction. The most general version of the
![]() $(C,F)$
-construction, including the versions from [Reference DanilenkoDa1, Reference del JuncodJ2] as particular cases, appeared in [Reference DanilenkoDa3]. However, [Reference DanilenkoDa3] deals only with measure preserving actions. In §§2.2–2.3 here, we define non-singular
$(C,F)$
-construction, including the versions from [Reference DanilenkoDa1, Reference del JuncodJ2] as particular cases, appeared in [Reference DanilenkoDa3]. However, [Reference DanilenkoDa3] deals only with measure preserving actions. In §§2.2–2.3 here, we define non-singular
![]() $(C,F)$
-actions. Section 2.2 is preliminary: we define
$(C,F)$
-actions. Section 2.2 is preliminary: we define
![]() $(C,F)$
-equivalence relations and related quasi-invariant
$(C,F)$
-equivalence relations and related quasi-invariant
![]() $(C,F)$
-measures. The non-singular
$(C,F)$
-measures. The non-singular
![]() $(C,F)$
-actions related to the
$(C,F)$
-actions related to the
![]() $(C,F)$
-equivalence relations and
$(C,F)$
-equivalence relations and
![]() $(C,F)$
-measures appear in §2.3. They include all the non-singular rank-one transformations (and actions of Abelian groups) that have been studied earlier in the literature: see [Reference AaronsonAa, Reference Adams, Friedman and SilvaAdFrSi, Reference DanilenkoDa1, Reference DanilenkoDa2, Reference Danilenko, Silva and MeyersDaSi, Reference Hamachi and SilvaHaSi] and references therein. The main result of §2 is the following (see Theorem 2.13).
$(C,F)$
-measures appear in §2.3. They include all the non-singular rank-one transformations (and actions of Abelian groups) that have been studied earlier in the literature: see [Reference AaronsonAa, Reference Adams, Friedman and SilvaAdFrSi, Reference DanilenkoDa1, Reference DanilenkoDa2, Reference Danilenko, Silva and MeyersDaSi, Reference Hamachi and SilvaHaSi] and references therein. The main result of §2 is the following (see Theorem 2.13).
Theorem A. Each non-singular
![]() $(C,F)$
-action of G is of rank one and each rank-one non-singular action of G is isomorphic to a
$(C,F)$
-action of G is of rank one and each rank-one non-singular action of G is isomorphic to a
![]() $(C,F)$
-action.
$(C,F)$
-action.
It is worth noting that if a probability preserving G-action is of rank one along a sequence
![]() $(F_n)_{n=1}^\infty $
of subsets in G, then G is amenable and
$(F_n)_{n=1}^\infty $
of subsets in G, then G is amenable and
![]() $(F_n)_{n=1}^\infty $
is left Følner (see Corollary 2.11(ii)).
$(F_n)_{n=1}^\infty $
is left Følner (see Corollary 2.11(ii)).
Important concepts of telescoping and reduction for the parameters of
![]() $(C,F)$
-actions are introduced in §2.4. They are used in §2.5 to construct continuous models of the non-singular
$(C,F)$
-actions are introduced in §2.4. They are used in §2.5 to construct continuous models of the non-singular
![]() $(C,F)$
-actions. We remind that the famous Jewett–Krieger theorem provides strictly ergodic models for the ergodic probability preserving
$(C,F)$
-actions. We remind that the famous Jewett–Krieger theorem provides strictly ergodic models for the ergodic probability preserving
![]() ${\mathbb Z}$
-actions. In [Reference YuasaYu], an analogue of this theorem was proved for the infinite measure preserving ergodic transformations. In the present paper, we prove the existence of Radon uniquely ergodic minimal topological models for the rank-one non-singular actions (see Theorem 2.19).
${\mathbb Z}$
-actions. In [Reference YuasaYu], an analogue of this theorem was proved for the infinite measure preserving ergodic transformations. In the present paper, we prove the existence of Radon uniquely ergodic minimal topological models for the rank-one non-singular actions (see Theorem 2.19).
Theorem B. If
![]() $(X,\mu ,(T_g)_{g\in R})$
is a non-singular G-action of rank one, then there are a Radon uniquely ergodic minimal free continuous G-action
$(X,\mu ,(T_g)_{g\in R})$
is a non-singular G-action of rank one, then there are a Radon uniquely ergodic minimal free continuous G-action
![]() $(R_g)_{g\in G}$
on a locally compact Cantor space Y, an R-quasi-invariant Radon measure
$(R_g)_{g\in G}$
on a locally compact Cantor space Y, an R-quasi-invariant Radon measure
![]() $\nu $
on Y and a measure preserving isomorphism
$\nu $
on Y and a measure preserving isomorphism
![]() $\phi $
of
$\phi $
of
![]() $(X,\mu )$
onto
$(X,\mu )$
onto
![]() $(Y,\nu )$
such that
$(Y,\nu )$
such that
![]() $\phi T_g\phi ^{-1}=R_g$
almost everywhere and the Radon–Nikodym derivative
$\phi T_g\phi ^{-1}=R_g$
almost everywhere and the Radon–Nikodym derivative
![]() $\rho _g:= {d\nu \circ R_g}/{d\nu }$
is a continuous mapping from Y to
$\rho _g:= {d\nu \circ R_g}/{d\nu }$
is a continuous mapping from Y to
![]() $\mathbb R_+^*$
for each
$\mathbb R_+^*$
for each
![]() $g\in G$
. Moreover,
$g\in G$
. Moreover,
![]() $\nu $
is the only (up to scaling) R-quasi-invariant Radon measure on Y whose Radon–Nikodym cocycle equals
$\nu $
is the only (up to scaling) R-quasi-invariant Radon measure on Y whose Radon–Nikodym cocycle equals
![]() $(\rho _g)_{g\in G}$
.
$(\rho _g)_{g\in G}$
.
We note that the continuity of the Radon–Nikodym derivatives was used essentially in [Reference Danilenko and del JuncoDadJ] for the almost continuous orbit classification of non-singular homeomorphisms of Krieger type III. Theorems A and B generalize respectively [Reference DanilenkoDa3, Theorem 1.6 and Corollary 1.9], where only measure preserving systems were under consideration.
In §§2.6 and 2.7, we discuss the case of non-singular
![]() ${\mathbb Z}$
-actions of rank one along intervals in more detail. It is shown in §2.6 that the
${\mathbb Z}$
-actions of rank one along intervals in more detail. It is shown in §2.6 that the
![]() $(C,F)$
-construction in this case is equivalent to the classical cutting-and-stacking with a single tower at every step of the construction. However, in contrast with the measure preserving case, the towers are now divided into subtowers of different width. It is explained in §2.7 how the underlying
$(C,F)$
-construction in this case is equivalent to the classical cutting-and-stacking with a single tower at every step of the construction. However, in contrast with the measure preserving case, the towers are now divided into subtowers of different width. It is explained in §2.7 how the underlying
![]() $(C,F)$
-parameters are used to present a rank-one non-singular transformation as a transformation built over a classical non-singular odometer of product type (called also Krieger’s adding machine) and under a piecewise constant function.
$(C,F)$
-parameters are used to present a rank-one non-singular transformation as a transformation built over a classical non-singular odometer of product type (called also Krieger’s adding machine) and under a piecewise constant function.
Section 3 is devoted to the description of finite factors of rank-one non-singular actions. We remind that a factor of a dynamical system is an invariant sub-
![]() $\sigma $
-algebra of measurable subsets. Equivalently, a factor of a system is a dynamical system which appears as the image of the original system under a non-singular equivariant mapping. Hence, the finite factors of an ergodic G-action correspond to the G-equivariant mappings onto homogeneous G-spaces
$\sigma $
-algebra of measurable subsets. Equivalently, a factor of a system is a dynamical system which appears as the image of the original system under a non-singular equivariant mapping. Hence, the finite factors of an ergodic G-action correspond to the G-equivariant mappings onto homogeneous G-spaces
![]() $G/\Gamma $
, where
$G/\Gamma $
, where
![]() $\Gamma $
is a cofinite subgroup in G. Each non-singular
$\Gamma $
is a cofinite subgroup in G. Each non-singular
![]() $(C,F)$
-action is parametrized by an underlying sequence
$(C,F)$
-action is parametrized by an underlying sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of
![]() $(C,F)$
-parameters, where
$(C,F)$
-parameters, where
![]() $C_n$
and
$C_n$
and
![]() $F_{n-1}$
are finite subsets of G,
$F_{n-1}$
are finite subsets of G,
![]() $\kappa _n$
is a probability on
$\kappa _n$
is a probability on
![]() $C_n$
and
$C_n$
and
![]() $\nu _{n-1}$
is measure on
$\nu _{n-1}$
is measure on
![]() $F_{n-1}$
for each
$F_{n-1}$
for each
![]() $n\in \mathbb N$
. These parameters have to satisfy some conditions listed in §2.3. The following is the main result of §3 (a stronger version of it is proved as Theorem 3.3; see also Remark 3.4).
$n\in \mathbb N$
. These parameters have to satisfy some conditions listed in §2.3. The following is the main result of §3 (a stronger version of it is proved as Theorem 3.3; see also Remark 3.4).
Theorem C. A non-singular
![]() $(C,F)$
-action T of G has a finite factor
$(C,F)$
-action T of G has a finite factor
![]() $G/\Gamma $
if and only there is a telescoping
$G/\Gamma $
if and only there is a telescoping
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of the
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of the
![]() $(C,F)$
-parameters of T and a coset
$(C,F)$
-parameters of T and a coset
![]() $g\Gamma \in G/\Gamma $
such that
$g\Gamma \in G/\Gamma $
such that
 $$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g\Gamma g^{-1}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g\Gamma g^{-1}\})<\infty. \end{align*} $$
An explicit formula for the factor mapping is obtained.
We note that if G is Abelian,
![]() $\Gamma \subset G$
is a cofinite subgroup and the homogeneous G-space
$\Gamma \subset G$
is a cofinite subgroup and the homogeneous G-space
![]() $G/\Gamma $
is a factor-space of an ergodic G-action T, then the corresponding factor-algebra of T is defined uniquely. This is no longer true for non-Abelain G: we provide an example of a rank-one G-action T and two T-invariant sub-
$G/\Gamma $
is a factor-space of an ergodic G-action T, then the corresponding factor-algebra of T is defined uniquely. This is no longer true for non-Abelain G: we provide an example of a rank-one G-action T and two T-invariant sub-
![]() $\sigma $
-algebras
$\sigma $
-algebras ![]() such that
such that ![]() and
and ![]() are isomorphic G-actions on finite spaces (Example 3.5).
are isomorphic G-actions on finite spaces (Example 3.5).
A criterion of total ergodicity for a non-singular
![]() $(C,F)$
-action in terms of the underlying
$(C,F)$
-action in terms of the underlying
![]() $(C,F)$
-parameters is obtained as a corollary from Theorem C (see Corollary 3.6).
$(C,F)$
-parameters is obtained as a corollary from Theorem C (see Corollary 3.6).
Starting from §4, we assume that G is residually finite. Section 4 consists of two subsections. In §4.1, we consider topological G-odometers as the projective limits of homogeneous G-spaces
![]() $G/\Gamma _n$
for a decreasing sequence
$G/\Gamma _n$
for a decreasing sequence ![]() of cofinite subgroups in G such that
of cofinite subgroups in G such that
![]() $\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=\{1_G\}$
. By a non-singular G-odometer, we mean a topological G-odometer endowed with a G-quasi-invariant measure. Topological properties of odometers are not of our primary interest in the present work. Measure theoretical odometers (for general groups) were under study in [Reference Danilenko and LemańczykDaLe, Reference Lightwood, Şahin and UgarcoviciLiSaUg], but only in the finite measure preserving case. In this paper, we study non-singular G-odometers. Some sufficient conditions for a non-singular odometer to be of rank one are found in Proposition 4.2. These conditions are satisfied for all known non-singular odometers (see Example 4.3). It is worth noting that there exist odometers which are not of rank one. Examples of non-rank-one probability preserving G-odometers for non-amenable G are given in Example 4.4 and for amenable G (including the Grigorchuk group) in Examples 4.5 and 4.6. However, each probability preserving G-odometer is a factor of an infinite measure preserving rank-one G-action (see Theorem 4.9 for a slightly stronger result):
$\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=\{1_G\}$
. By a non-singular G-odometer, we mean a topological G-odometer endowed with a G-quasi-invariant measure. Topological properties of odometers are not of our primary interest in the present work. Measure theoretical odometers (for general groups) were under study in [Reference Danilenko and LemańczykDaLe, Reference Lightwood, Şahin and UgarcoviciLiSaUg], but only in the finite measure preserving case. In this paper, we study non-singular G-odometers. Some sufficient conditions for a non-singular odometer to be of rank one are found in Proposition 4.2. These conditions are satisfied for all known non-singular odometers (see Example 4.3). It is worth noting that there exist odometers which are not of rank one. Examples of non-rank-one probability preserving G-odometers for non-amenable G are given in Example 4.4 and for amenable G (including the Grigorchuk group) in Examples 4.5 and 4.6. However, each probability preserving G-odometer is a factor of an infinite measure preserving rank-one G-action (see Theorem 4.9 for a slightly stronger result):
Theorem D. For a topological G-odometer O defined on a compact space Y, there exist:
-
• a rank-one measure preserving continuous G-action T on a locally compact Cantor space X equipped with a
 $\sigma $
-finite measure
$\sigma $
-finite measure
 $\mu $
; and
$\mu $
; and -
• a G-equivariant continuous mapping
 $\pi :X\to Y$
$\pi :X\to Y$
such that O is a factor of T and the measure
![]() $\mu \circ \pi ^{-1}$
is equivalent (that is, has the same ideal of subsets of zero measure) to the Haar measure on Y.
$\mu \circ \pi ^{-1}$
is equivalent (that is, has the same ideal of subsets of zero measure) to the Haar measure on Y.
Thus, a factor of a rank-one non-singular action is not necessarily of rank one. This is in contrast with the classical case of rank-one finite measure preserving
![]() ${\mathbb Z}$
-actions [Reference FerencziFe]. Theorem 4.9 is about an interplay between odometer factors and an ‘unordered’ sequence of finite factors for an ergodic G-action. This theorem is trivial in the case where G is Abelian.
${\mathbb Z}$
-actions [Reference FerencziFe]. Theorem 4.9 is about an interplay between odometer factors and an ‘unordered’ sequence of finite factors for an ergodic G-action. This theorem is trivial in the case where G is Abelian.
Non-singular normal covers for non-singular odometers are introduced in §4.2. The existence of non-singular normal covers is proved in Proposition 4.11.
In §4, we study odometer factors of non-singular
![]() $(C,F)$
-actions. The main result of the paper is the following (see Theorem 5.4).
$(C,F)$
-actions. The main result of the paper is the following (see Theorem 5.4).
Theorem E. Let
![]() $(X,\mu ,T)$
be the non-singular
$(X,\mu ,T)$
be the non-singular
![]() $(C,F)$
-action of G associated with a sequence of
$(C,F)$
-action of G associated with a sequence of
![]() $(C,F)$
-parameters
$(C,F)$
-parameters
![]() $\mathcal T$
. Let O be the topological G-odometer defined on the projective space
$\mathcal T$
. Let O be the topological G-odometer defined on the projective space
![]() $Y=\projlim _{n\to \infty }G/\Gamma _n$
corresponding to a nested sequence
$Y=\projlim _{n\to \infty }G/\Gamma _n$
corresponding to a nested sequence ![]() of cofinite subgroups in G such that
of cofinite subgroups in G such that
![]() $\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=\{1_G\}$
. A measurable G-equivariant mapping
$\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=\{1_G\}$
. A measurable G-equivariant mapping
![]() $\pi :X\to Y$
exists if and only if there are a telescoping
$\pi :X\to Y$
exists if and only if there are a telescoping
![]() $\mathcal T'=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of
$\mathcal T'=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
of
![]() $\mathcal T$
and an element
$\mathcal T$
and an element
![]() $(g_n\Gamma _n)_{n=1}^\infty \in Y$
such that
$(g_n\Gamma _n)_{n=1}^\infty \in Y$
such that
 $$ \begin{align*} \sum_{n=1}^\infty\kappa_n(\{c\in C_n\mid c\not\in g_n\Gamma_n g_n^{-1}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty\kappa_n(\{c\in C_n\mid c\not\in g_n\Gamma_n g_n^{-1}\})<\infty. \end{align*} $$
An explicit formula for
![]() $\pi $
is obtained. Necessary and sufficient conditions for
$\pi $
is obtained. Necessary and sufficient conditions for
![]() $\pi $
to be an isomorphism of
$\pi $
to be an isomorphism of
![]() $(X,\mu , T)$
onto
$(X,\mu , T)$
onto
![]() $(Y,O,\mu \circ \pi ^{-1})$
are given in terms of
$(Y,O,\mu \circ \pi ^{-1})$
are given in terms of
![]() $\mathcal T'$
.
$\mathcal T'$
.
It is worth noting that each rank-one non-singular action T is parametrized by the
![]() $(C,F)$
-parameters
$(C,F)$
-parameters
![]() $\mathcal T$
(see Theorem A) in a highly non-unique way. However, the properties of
$\mathcal T$
(see Theorem A) in a highly non-unique way. However, the properties of
![]() $\mathcal T$
specified in the statement of Theorem E (to determine an odometer factor O or an isomorphism of T with O) are independent on the choice of
$\mathcal T$
specified in the statement of Theorem E (to determine an odometer factor O or an isomorphism of T with O) are independent on the choice of
![]() $\mathcal T$
. Hence, Theorem E can be considered as a contribution to the classification problem for the rank-one non-singular systems.
$\mathcal T$
. Hence, Theorem E can be considered as a contribution to the classification problem for the rank-one non-singular systems.
As a corollary from Theorem E, criteria for a
![]() $(C,F)$
-action to have an odometer factor or to be isomorphic to an odometer factor in terms of the underlying
$(C,F)$
-action to have an odometer factor or to be isomorphic to an odometer factor in terms of the underlying
![]() $(C,F)$
-parameters are obtained in Corollaries 5.6 and 5.7, respectively. Corollary 5.8 provides minimal Radon uniquely ergodic models for the rank-one non-singular extensions of non-singular odometers. This corollary can be interpreted as a ‘relative’ counterpart of Theorem B.
$(C,F)$
-parameters are obtained in Corollaries 5.6 and 5.7, respectively. Corollary 5.8 provides minimal Radon uniquely ergodic models for the rank-one non-singular extensions of non-singular odometers. This corollary can be interpreted as a ‘relative’ counterpart of Theorem B.
Theorem F. Let
![]() $(X,\mu ,T)$
be a rank-one non-singular G-action,
$(X,\mu ,T)$
be a rank-one non-singular G-action,
![]() $(Y,\nu ,O)$
a non-singular G-odometer and
$(Y,\nu ,O)$
a non-singular G-odometer and
![]() $\pi :X\to Y$
a G-equivariant mapping with
$\pi :X\to Y$
a G-equivariant mapping with
![]() $\mu \circ \pi ^{-1}=\nu $
. Then there exist a locally compact Cantor space
$\mu \circ \pi ^{-1}=\nu $
. Then there exist a locally compact Cantor space
![]() $\widetilde X$
, a minimal Radon uniquely ergodic free continuous G-action
$\widetilde X$
, a minimal Radon uniquely ergodic free continuous G-action
![]() $\widetilde T$
on
$\widetilde T$
on
![]() $\widetilde X$
, a continuous G-equivariant mapping
$\widetilde X$
, a continuous G-equivariant mapping
![]() $\widetilde \pi :X\to Y$
and a Borel isomorphism
$\widetilde \pi :X\to Y$
and a Borel isomorphism
![]() $R:X\to \widetilde X$
such that
$R:X\to \widetilde X$
such that
![]() $\mu \circ R^{-1}$
is a Radon measure on
$\mu \circ R^{-1}$
is a Radon measure on
![]() $\widetilde X$
,
$\widetilde X$
,
![]() ${RT_gR^{-1}=\widetilde T_g}$
for each
${RT_gR^{-1}=\widetilde T_g}$
for each
![]() $g\in G$
, the Radon–Nikodym derivative
$g\in G$
, the Radon–Nikodym derivative
![]() $\rho _g:= {d(\mu \circ R^{-1})\circ \widetilde T_g}/{d(\mu \circ R^{-1})}$
is a continuous mapping from
$\rho _g:= {d(\mu \circ R^{-1})\circ \widetilde T_g}/{d(\mu \circ R^{-1})}$
is a continuous mapping from
![]() $\widetilde X$
to
$\widetilde X$
to
![]() $\mathbb R^*_+$
for each
$\mathbb R^*_+$
for each
![]() $g\in G$
and
$g\in G$
and
![]() $\widetilde \pi \circ R=\pi $
. Moreover,
$\widetilde \pi \circ R=\pi $
. Moreover,
![]() $\widetilde T$
is also Radon
$\widetilde T$
is also Radon
![]() $(\rho _g)_{g\in G}$
-uniquely ergodic.
$(\rho _g)_{g\in G}$
-uniquely ergodic.
It follows from the Glimm–Effros theorem (see [Reference Danilenko, Silva and MeyersDaSi, Reference EffrosEf]) that each topological odometer
![]() $(Y,O)$
(in fact, each topological G-action with a recurrent point) has uncountably many ergodic quasi-invariant measures. However, the space of these measures is huge and ‘wild’ to describe it in good parameters. Using Theorems E and F, we can isolate a good class of ergodic finite quasi-invariant measures that admits a good parametrization. This is the class of factor measures on Y for all rank-one non-singular G-actions for which Y is a factor. Every such measure can be parametrized by the
$(Y,O)$
(in fact, each topological G-action with a recurrent point) has uncountably many ergodic quasi-invariant measures. However, the space of these measures is huge and ‘wild’ to describe it in good parameters. Using Theorems E and F, we can isolate a good class of ergodic finite quasi-invariant measures that admits a good parametrization. This is the class of factor measures on Y for all rank-one non-singular G-actions for which Y is a factor. Every such measure can be parametrized by the
![]() $(C,F)$
-parameters (see Corollary 5.9).
$(C,F)$
-parameters (see Corollary 5.9).
Section 6 is devoted completely to construction of five concrete rank-one actions with odometer factors and interesting properties. In §6.1, we continue studying the example of non-odometer rank-one probability preserving
![]() ${\mathbb Z}$
-action
${\mathbb Z}$
-action
![]() $(X,\mu ,T)$
from [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. It was shown there that the maximal odometer factor
$(X,\mu ,T)$
from [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. It was shown there that the maximal odometer factor ![]() of T is non-trivial and isomorphic to the classical 2-adic odometer. We prove that
of T is non-trivial and isomorphic to the classical 2-adic odometer. We prove that ![]() is the Kronecker factor of T and that T is an uncountable-to-one extension of
is the Kronecker factor of T and that T is an uncountable-to-one extension of ![]() . It follows, in particular, that the spectrum of T has a continuous component. In §6.2, we consider non-singular counterparts of the aforementioned system
. It follows, in particular, that the spectrum of T has a continuous component. In §6.2, we consider non-singular counterparts of the aforementioned system
![]() $(X,\mu ,T)$
. In particular, for each
$(X,\mu ,T)$
. In particular, for each
![]() $\unicode{x3bb} \in [0,1]$
, we construct a measure
$\unicode{x3bb} \in [0,1]$
, we construct a measure
![]() $\mu _\unicode{x3bb} $
on X such that:
$\mu _\unicode{x3bb} $
on X such that:
-
• the triple
 $(X,\mu _\unicode{x3bb} , T)$
is a rank-one non-singular system of Krieger type III
$(X,\mu _\unicode{x3bb} , T)$
is a rank-one non-singular system of Krieger type III
 $_{\unicode{x3bb}} $
;
$_{\unicode{x3bb}} $
; -
•
 $(X,\mu _\unicode{x3bb} , T)$
has a factor
$(X,\mu _\unicode{x3bb} , T)$
has a factor  which is isomorphic to the probability preserving 2-adic odometer;
which is isomorphic to the probability preserving 2-adic odometer; -
•
 is the maximal (in the class of non-singular odometers) factor of
is the maximal (in the class of non-singular odometers) factor of
 $(X,\mu _\unicode{x3bb} , T)$
;
$(X,\mu _\unicode{x3bb} , T)$
; -
• the extension
 is uncountable-to-one (mod
is uncountable-to-one (mod
 $\mu _\unicode{x3bb} $
).
$\mu _\unicode{x3bb} $
).
In the III
![]() $_{0}$
-case, we extend this result to systems whose associated flow is an arbitrary finitary AT in the sense of Connes and Woods [Reference Connes and WoodsCoWo]. In §6.3, we provide an example of rank-one
$_{0}$
-case, we extend this result to systems whose associated flow is an arbitrary finitary AT in the sense of Connes and Woods [Reference Connes and WoodsCoWo]. In §6.3, we provide an example of rank-one
![]() ${\mathbb Z}^2$
-action
${\mathbb Z}^2$
-action
![]() $T=(T_{g})_{g\in {\mathbb Z}^2}$
such that the generators
$T=(T_{g})_{g\in {\mathbb Z}^2}$
such that the generators
![]() $T_{(0,1)}$
and
$T_{(0,1)}$
and
![]() $T_{(1,0)}$
have
$T_{(1,0)}$
have
![]() ${\mathbb Z}$
-odometer factors, but T has no
${\mathbb Z}$
-odometer factors, but T has no
![]() ${\mathbb Z}^2$
-odometer factor. Another construction of such an action has appeared earlier in [Reference Johnson and McClendonJoMc, §6], but our example is much simpler. In §6.4, we construct a rank-one action T of the Heisenberg group
${\mathbb Z}^2$
-odometer factor. Another construction of such an action has appeared earlier in [Reference Johnson and McClendonJoMc, §6], but our example is much simpler. In §6.4, we construct a rank-one action T of the Heisenberg group
![]() $H_3({\mathbb Z})$
which has an odometer factor
$H_3({\mathbb Z})$
which has an odometer factor ![]() , but which is not isomorphic to any odometer action. We show there that
, but which is not isomorphic to any odometer action. We show there that ![]() is the maximal odometer factor of T and the extension
is the maximal odometer factor of T and the extension ![]() is uncountable-to-one. In §6.5, we provide an example of non-normal
is uncountable-to-one. In §6.5, we provide an example of non-normal
![]() $H_3({\mathbb Z})$
-odometer which is canonically isomorphic to a normal odometer.
$H_3({\mathbb Z})$
-odometer which is canonically isomorphic to a normal odometer.
The final §7 is devoted to the article [Reference Johnson and McClendonJoMc] which appeared in the course of our work on the present paper. The purpose of [Reference Johnson and McClendonJoMc] is the same as ours: to generalize [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. However, only finite measure preserving actions of amenable groups and only normal odometers are studied in [Reference Johnson and McClendonJoMc]. Therefore, in §7, we discuss the results of [Reference Johnson and McClendonJoMc] and compare them with results of the present paper.
2. Rank-one non-singular actions of countable groups and
 $(C,F)$
-construction
$(C,F)$
-construction
2.1. Non-singular actions of rank one
Let G be a discrete infinite countable group. Let
![]() $T=(T_g)_{g\in G}$
be a free non-singular action of G on a standard
$T=(T_g)_{g\in G}$
be a free non-singular action of G on a standard
![]() $\sigma $
-finite non-atomic measure space
$\sigma $
-finite non-atomic measure space ![]() . By a Rokhlin tower for T, we mean a pair
. By a Rokhlin tower for T, we mean a pair
![]() $(B,F)$
, where
$(B,F)$
, where ![]() with
with
![]() $0<\mu (B)<\infty $
and F is a finite subset of G with
$0<\mu (B)<\infty $
and F is a finite subset of G with
![]() $1_G\in F$
such that:
$1_G\in F$
such that:
-
• the subsets
 $T_fB$
,
$T_fB$
,
 $f\in F$
, are mutually disjoint;
$f\in F$
, are mutually disjoint; -
• the Radon–Nikodym derivative
 ${d\mu \circ T_f}/{d\mu }$
is constant on B for each
${d\mu \circ T_f}/{d\mu }$
is constant on B for each
 $f\in F$
.
$f\in F$
.
Given a Rokhlin tower
![]() $(B,F)$
, we let
$(B,F)$
, we let ![]() . Of course,
. Of course,
![]() ${\mu (X_{B,F})<\infty }$
. By
${\mu (X_{B,F})<\infty }$
. By
![]() $\xi _{B,F}$
, we mean the finite partition of
$\xi _{B,F}$
, we mean the finite partition of
![]() $X_{B,F}$
into the subsets
$X_{B,F}$
into the subsets
![]() $T_fB$
,
$T_fB$
,
![]() $f\in F$
. If
$f\in F$
. If
![]() $x\in T_fB$
, then we set
$x\in T_fB$
, then we set
![]() $O_{B,F}(x):=\{T_gx\mid g\in Ff^{-1}\}$
.
$O_{B,F}(x):=\{T_gx\mid g\in Ff^{-1}\}$
.
Definition 2.1. Let ![]() be an increasing sequence of finite subsets in G. We say that T is of rank-one along
be an increasing sequence of finite subsets in G. We say that T is of rank-one along
![]() $(F_n)_{n=0}^\infty $
if there is a decreasing sequence
$(F_n)_{n=0}^\infty $
if there is a decreasing sequence ![]() of subsets of positive measure in X such that
of subsets of positive measure in X such that
![]() $(B_n,F_n)$
is a Rokhlin tower for T for each
$(B_n,F_n)$
is a Rokhlin tower for T for each
![]() $n\in \mathbb N$
and:
$n\in \mathbb N$
and:
-
(i)
 $\xi _{B_n,F_n}\prec \xi _{B_{n+1},F_{n+1}}$
for each
$\xi _{B_n,F_n}\prec \xi _{B_{n+1},F_{n+1}}$
for each
 $n\ge 0$
and
$n\ge 0$
and
 $\bigvee _{n=0}^\infty \xi _{B_n,F_n}$
is the partition of X into singletons (mod 0);
$\bigvee _{n=0}^\infty \xi _{B_n,F_n}$
is the partition of X into singletons (mod 0); -
(ii)
 $\{T_gx\mid g\in G\}=\bigcup _{n=1}^\infty O_{B_n,F_n}(x)$
for almost every (a.e.)
$\{T_gx\mid g\in G\}=\bigcup _{n=1}^\infty O_{B_n,F_n}(x)$
for almost every (a.e.)
 $x\in X$
.
$x\in X$
.
It follows from property (i) that ![]() and
and
![]() ${\bigcup _{n=0}^\infty X_{B_n,F_n}=X}$
. The piecewise constant property of the Radon–Nikodym derivative on the Rokhlin towers yields that:
${\bigcup _{n=0}^\infty X_{B_n,F_n}=X}$
. The piecewise constant property of the Radon–Nikodym derivative on the Rokhlin towers yields that:
-
(iii) if
 $T_cB_{n+1}\subset B_{n}$
for some
$T_cB_{n+1}\subset B_{n}$
for some
 $c\in F_{n+1}$
, then
$c\in F_{n+1}$
, then  $$ \begin{align*} \frac{\mu(T_{fc}B_{n+1})}{\mu(T_fB_n)}=\frac{\mu(T_cB_{n+1})}{\mu(B_n)}\quad\text{for each } f\in F_n \text{ and } n\ge 0. \end{align*} $$
$$ \begin{align*} \frac{\mu(T_{fc}B_{n+1})}{\mu(T_fB_n)}=\frac{\mu(T_cB_{n+1})}{\mu(B_n)}\quad\text{for each } f\in F_n \text{ and } n\ge 0. \end{align*} $$
Proposition 2.2. Let T satisfy condition (i) from Definition 2.1. Then T is ergodic. In particular, every rank-one non-singular action is ergodic.
Proof. Let two subsets ![]() be of positive measure. It follows from condition (i) that there are
be of positive measure. It follows from condition (i) that there are
![]() $n>0$
and
$n>0$
and
![]() $f_1,f_2\in F_n$
such that
$f_1,f_2\in F_n$
such that
As
![]() $(B_n,F_n)$
is a Rokhlin tower,
$(B_n,F_n)$
is a Rokhlin tower,
![]() $T_{f_2f_1^{-1}}T_{f_1}B_n=T_{f_2}B_n$
and
$T_{f_2f_1^{-1}}T_{f_1}B_n=T_{f_2}B_n$
and
 $$ \begin{align*} \frac{d\mu\circ T_{f_2f_1^{-1}}}{d\mu}(x) = \frac{\mu(T_{f_2}B_n)}{\mu(T_{f_1}B_n)}\quad\text{at a.e. } x\in A_1. \end{align*} $$
$$ \begin{align*} \frac{d\mu\circ T_{f_2f_1^{-1}}}{d\mu}(x) = \frac{\mu(T_{f_2}B_n)}{\mu(T_{f_1}B_n)}\quad\text{at a.e. } x\in A_1. \end{align*} $$
It follows that
 $$ \begin{align*} \begin{aligned} \mu(T_{f_2f_1^{-1}}A_1\cap T_{f_2}B_n)&= \mu (T_{f_2f_1^{-1}}(A_1\cap T_{f_1}B_n))\\ &= \mu(A_1\cap T_{f_1}B_n) \frac{\mu(T_{f_2}B_n)}{\mu(T_{f_1}B_n)}\\ &>0.9\mu(T_{f_2B_n}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mu(T_{f_2f_1^{-1}}A_1\cap T_{f_2}B_n)&= \mu (T_{f_2f_1^{-1}}(A_1\cap T_{f_1}B_n))\\ &= \mu(A_1\cap T_{f_1}B_n) \frac{\mu(T_{f_2}B_n)}{\mu(T_{f_1}B_n)}\\ &>0.9\mu(T_{f_2B_n}). \end{aligned} \end{align*} $$
Therefore,
![]() $\mu (T_{f_2f_1^{-1}}A_1\cap T_{f_2}B_n\cap A_2)>0.8\mu (T_{f_2}B_n)$
. Hence,
$\mu (T_{f_2f_1^{-1}}A_1\cap T_{f_2}B_n\cap A_2)>0.8\mu (T_{f_2}B_n)$
. Hence,
![]() $\mu (T_{f_2f_1^{-1}}A_1\cap A_2)>0$
, as desired.
$\mu (T_{f_2f_1^{-1}}A_1\cap A_2)>0$
, as desired.
2.2.
 $(C,F)$
-equivalence relations and non-singular
$(C,F)$
-equivalence relations and non-singular
 $(C,F)$
-measures
$(C,F)$
-measures
Fix two sequences
![]() $(F_n)_{n\geq 0}$
and
$(F_n)_{n\geq 0}$
and
![]() $(C_n)_{n\geq 1}$
of finite subsets in G such that
$(C_n)_{n\geq 1}$
of finite subsets in G such that
![]() $F_{0} = \{1_G\}$
and for each
$F_{0} = \{1_G\}$
and for each
![]() $n>0$
,
$n>0$
,
 $$ \begin{align} \begin{aligned} & 1_G\in F_n\cap C_n, \ \#C_{n}> 1, \\ &F_{n} C_{n+1}\subset F_{n+1},\\ &F_{n} c\cap F_{n} c' = \emptyset\quad\text{if } c, c'\in C_{n+1}\text{ and } c \neq c'. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & 1_G\in F_n\cap C_n, \ \#C_{n}> 1, \\ &F_{n} C_{n+1}\subset F_{n+1},\\ &F_{n} c\cap F_{n} c' = \emptyset\quad\text{if } c, c'\in C_{n+1}\text{ and } c \neq c'. \end{aligned} \end{align} $$
We let ![]() and endow this set with the infinite product topology. Then
and endow this set with the infinite product topology. Then
![]() $X_n$
is a compact Cantor space. The mapping
$X_n$
is a compact Cantor space. The mapping
is a continuous embedding of
![]() $X_n$
into
$X_n$
into
![]() $X_{n+1}$
. Therefore, the topological inductive limit X of the sequence
$X_{n+1}$
. Therefore, the topological inductive limit X of the sequence
![]() $(X_n)_{n\geq 0}$
is well defined. Moreover, X is a locally compact Cantor space. Given a subset
$(X_n)_{n\geq 0}$
is well defined. Moreover, X is a locally compact Cantor space. Given a subset
![]() $A\subset F_n$
, we let
$A\subset F_n$
, we let
and call this set an n-cylinder in X. It is open and compact in X. For brevity, we will write
![]() $[f]_n$
for
$[f]_n$
for
![]() $[\{f\}]_n$
for an element
$[\{f\}]_n$
for an element
![]() $f\in F_n$
.
$f\in F_n$
.
We remind that two points
![]() $x=(f_n,c_{n+1},\ldots )$
and
$x=(f_n,c_{n+1},\ldots )$
and
![]() $x'=(f_n',c_{n+1}',\ldots )$
of
$x'=(f_n',c_{n+1}',\ldots )$
of
![]() $X_n$
are tail equivalent if there is
$X_n$
are tail equivalent if there is
![]() $N>n$
such that
$N>n$
such that
![]() $c_l=c_{l}'$
for each
$c_l=c_{l}'$
for each
![]() $l>N$
. We thus obtain the tail equivalence relation on
$l>N$
. We thus obtain the tail equivalence relation on
![]() $X_n$
.
$X_n$
.
Definition 2.3. [Reference DanilenkoDa3]
The
![]() $(C,F)$
-equivalence relation (or the tail equivalence relation)
$(C,F)$
-equivalence relation (or the tail equivalence relation)
![]() $\mathcal R$
on X is defined as follows: for each
$\mathcal R$
on X is defined as follows: for each
![]() $n\ge 0$
, the restriction of
$n\ge 0$
, the restriction of
![]() $\mathcal R$
to
$\mathcal R$
to
![]() $X_n$
is the tail equivalence relation on
$X_n$
is the tail equivalence relation on
![]() $X_n$
.
$X_n$
.
The following properties of
![]() $\mathcal R$
are easy to check:
$\mathcal R$
are easy to check:
-
• each
 $\mathcal R$
-class is countable;
$\mathcal R$
-class is countable; -
•
 $\mathcal R$
is minimal, that is, the
$\mathcal R$
is minimal, that is, the
 $\mathcal R$
-class of every point is dense in X;
$\mathcal R$
-class of every point is dense in X; -
•
 $\mathcal R$
is hyperfinite, that is, there is a sequence
$\mathcal R$
is hyperfinite, that is, there is a sequence
 $(\mathcal S_n)_{n=1}^\infty $
of subrelations of
$(\mathcal S_n)_{n=1}^\infty $
of subrelations of
 $\mathcal R$
such that
$\mathcal R$
such that  ,
,
 $\bigcup _{n=1}^\infty \mathcal S_n=\mathcal R$
and
$\bigcup _{n=1}^\infty \mathcal S_n=\mathcal R$
and
 $\#\mathcal S_n(x)<\infty $
for each
$\#\mathcal S_n(x)<\infty $
for each
 $x\in X$
and
$x\in X$
and
 $n > 0$
. Indeed, we can define
$n > 0$
. Indeed, we can define
 $\mathcal S_n$
by the following:
$\mathcal S_n$
by the following:
 $(x,y)\in \mathcal S_n$
if either
$(x,y)\in \mathcal S_n$
if either
 $x,y\not \in X_n$
and
$x,y\not \in X_n$
and
 $x=y$
or
$x=y$
or
 $x=(f_n,c_{n+1},\ldots )\in X_n,y=(f_n',c_{n+1}',\ldots )\in X_n$
and
$x=(f_n,c_{n+1},\ldots )\in X_n,y=(f_n',c_{n+1}',\ldots )\in X_n$
and
 $c_m=c_m'$
for all
$c_m=c_m'$
for all
 $m>n$
.
$m>n$
.
We recall that the full group
![]() $[\mathcal R]$
of
$[\mathcal R]$
of
![]() $\mathcal R$
is the group of all Borel bijections
$\mathcal R$
is the group of all Borel bijections
![]() $\gamma :X\to X$
such that
$\gamma :X\to X$
such that
![]() $(x,\gamma x)\in \mathcal R$
for each
$(x,\gamma x)\in \mathcal R$
for each
![]() $x\in X$
. A Borel measure
$x\in X$
. A Borel measure
![]() $\mu $
on X is called
$\mu $
on X is called
![]() $\mathcal R$
-quasi-invariant if
$\mathcal R$
-quasi-invariant if
![]() $\mu \circ \gamma \sim \mu $
for each
$\mu \circ \gamma \sim \mu $
for each
![]() $\gamma \in [\mathcal R]$
. Then there is a Borel mapping
$\gamma \in [\mathcal R]$
. Then there is a Borel mapping
![]() $\rho _\mu :\mathcal R\to \mathbb R^*_+$
such that
$\rho _\mu :\mathcal R\to \mathbb R^*_+$
such that
and
![]() $\rho _\mu (\gamma x,x)= ({d\mu \circ \gamma }/{d\mu })(x)$
at a.e.
$\rho _\mu (\gamma x,x)= ({d\mu \circ \gamma }/{d\mu })(x)$
at a.e.
![]() $x\in X$
for each
$x\in X$
for each
![]() $\gamma \in [\mathcal R]$
. The mapping
$\gamma \in [\mathcal R]$
. The mapping
![]() $\rho _\mu $
is called the Radon–Nikodym cocycle of
$\rho _\mu $
is called the Radon–Nikodym cocycle of
![]() $(\mathcal R,\mu )$
.
$(\mathcal R,\mu )$
.
Suppose that for each
![]() $n\in \mathbb N$
, a non-degenerated probability measure
$n\in \mathbb N$
, a non-degenerated probability measure
![]() $\kappa _n$
on
$\kappa _n$
on
![]() $C_n$
is given. We now let
$C_n$
is given. We now let ![]() , where
, where
![]() $\nu _0$
is the Dirac measure supported at
$\nu _0$
is the Dirac measure supported at
![]() $1_G$
. Then,
$1_G$
. Then,
![]() $\mu _0$
is an
$\mu _0$
is an
![]() $(\mathcal R\restriction X_0)$
-quasi-invariant probability on
$(\mathcal R\restriction X_0)$
-quasi-invariant probability on
![]() $X_0$
. Of course,
$X_0$
. Of course,
![]() $\mu _0$
is non-atomic if and only if
$\mu _0$
is non-atomic if and only if
By the Kolmogorov 0-1 law,
![]() $(\mathcal R\restriction X_0)$
is ergodic on the probability space
$(\mathcal R\restriction X_0)$
is ergodic on the probability space
![]() $(X_0,\mu _0)$
. There are many ways to extend
$(X_0,\mu _0)$
. There are many ways to extend
![]() $\mu _0$
to an
$\mu _0$
to an
![]() $\mathcal R$
-quasi-invariant measure on X. However, all such measures will be mutually equivalent. Select for each
$\mathcal R$
-quasi-invariant measure on X. However, all such measures will be mutually equivalent. Select for each
![]() $n\in \mathbb N$
a non-degenerated finite measure
$n\in \mathbb N$
a non-degenerated finite measure
![]() $\nu _n$
on
$\nu _n$
on
![]() $F_n$
such that
$F_n$
such that
It is often convenient to consider
![]() $\nu _n$
and
$\nu _n$
and
![]() $\kappa _n$
as finite measures on G supported on
$\kappa _n$
as finite measures on G supported on
![]() $F_n$
and
$F_n$
and
![]() $C_{n}$
, respectively. Then equation (2.3) means that
$C_{n}$
, respectively. Then equation (2.3) means that
![]() $\nu _{n+1}\restriction F_nC_{n+1}=\nu _n*\kappa _{n+1}$
, where the symbol
$\nu _{n+1}\restriction F_nC_{n+1}=\nu _n*\kappa _{n+1}$
, where the symbol
![]() $*$
means the convolution. We now define a Borel measure
$*$
means the convolution. We now define a Borel measure
![]() $\mu $
on X by setting
$\mu $
on X by setting
It is straightforward to verify that
![]() $\mu $
is a well-defined
$\mu $
is a well-defined
![]() $\sigma $
-finite Radon measure. Moreover,
$\sigma $
-finite Radon measure. Moreover,
![]() $\mu $
is
$\mu $
is
![]() $\mathcal R$
-quasi-invariant and
$\mathcal R$
-quasi-invariant and
 $$ \begin{align*} \rho_\mu(x,y)=\frac{\nu_n(f_n)}{\nu_n(f^{\prime}_n)}\prod_{m>n}\frac{\kappa_m(c_m)}{\kappa_m(c_m')}, \end{align*} $$
$$ \begin{align*} \rho_\mu(x,y)=\frac{\nu_n(f_n)}{\nu_n(f^{\prime}_n)}\prod_{m>n}\frac{\kappa_m(c_m)}{\kappa_m(c_m')}, \end{align*} $$
whenever
![]() $x=(f_n,c_{n+1},\ldots )$
and
$x=(f_n,c_{n+1},\ldots )$
and
![]() $y=(f_n',c_{n+1}',\ldots )$
are
$y=(f_n',c_{n+1}',\ldots )$
are
![]() $\mathcal R$
-equivalent points that belong to
$\mathcal R$
-equivalent points that belong to ![]() for some
for some
![]() $n>0$
.
$n>0$
.
The following definition extends [Reference DanilenkoDa1, Definition 4.2], where the case of Abelian G was considered.
Definition 2.4. If equations (2.2) and (2.3) hold, then we call
![]() $\mu $
the
$\mu $
the
![]() $(C,F)$
-measure on X determined by
$(C,F)$
-measure on X determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
.
$(\nu _n)_{n=0}^\infty $
.
Consider another sequence
![]() $(\nu _n')_{n=0}^\infty $
of non-degenerated measures on
$(\nu _n')_{n=0}^\infty $
of non-degenerated measures on
![]() $(F_n)_{n=0}^\infty $
(in n) such that
$(F_n)_{n=0}^\infty $
(in n) such that
![]() $\nu _0'$
is the Dirac measure supported at
$\nu _0'$
is the Dirac measure supported at
![]() $1_G$
and
$1_G$
and
![]() $\nu _{n+1}'(fc)=\nu _n'(f)\kappa _{n+1}(c)$
for each
$\nu _{n+1}'(fc)=\nu _n'(f)\kappa _{n+1}(c)$
for each
![]() $f\in F_n$
and
$f\in F_n$
and
![]() $c\in C_{n+1}$
for each
$c\in C_{n+1}$
for each
![]() $n>0$
. Then, the
$n>0$
. Then, the
![]() $(C,F)$
-measure
$(C,F)$
-measure
![]() $\mu '$
determined by
$\mu '$
determined by
![]() $(\kappa _n)_{n=1}^\infty $
, and
$(\kappa _n)_{n=1}^\infty $
, and
![]() $(\nu _n')_{n=0}^\infty $
is equivalent to
$(\nu _n')_{n=0}^\infty $
is equivalent to
![]() $\mu $
and
$\mu $
and
 $$ \begin{align*} \frac{d\mu'}{d\mu}(x)=\frac{\nu_n'(f_n)}{\nu_n(f_n)}\quad\text{if } x=(f_n,\ldots)\in X_n. \end{align*} $$
$$ \begin{align*} \frac{d\mu'}{d\mu}(x)=\frac{\nu_n'(f_n)}{\nu_n(f_n)}\quad\text{if } x=(f_n,\ldots)\in X_n. \end{align*} $$
Another useful observation is that given
![]() $(\kappa _n)_{n=1}^\infty $
, we can always find
$(\kappa _n)_{n=1}^\infty $
, we can always find
![]() $(\nu _n)_{n=0}^\infty $
satisfying equation (2.3). Thus, the equivalence class of a non-singular
$(\nu _n)_{n=0}^\infty $
satisfying equation (2.3). Thus, the equivalence class of a non-singular
![]() $(C,F)$
-measure is completely determined by
$(C,F)$
-measure is completely determined by
![]() $(\kappa _n)_{n=1}^\infty $
alone. In particular, we may always replace a
$(\kappa _n)_{n=1}^\infty $
alone. In particular, we may always replace a
![]() $\sigma $
-finite non-singular
$\sigma $
-finite non-singular
![]() $(C,F)$
-measure with an equivalent finite non-singular
$(C,F)$
-measure with an equivalent finite non-singular
![]() $(C,F)$
-measure.
$(C,F)$
-measure.
Remark 2.5. We note that
![]() $\mathcal R$
is Radon uniquely ergodic, that is, there is a unique
$\mathcal R$
is Radon uniquely ergodic, that is, there is a unique
![]() $\mathcal R$
-invariant Radon measure
$\mathcal R$
-invariant Radon measure
![]() $\xi $
on X such that
$\xi $
on X such that
![]() $\xi (X_0)=1$
. We call it the Haar measure for
$\xi (X_0)=1$
. We call it the Haar measure for
![]() $\mathcal R$
. It is
$\mathcal R$
. It is
![]() $\sigma $
-finite. Let
$\sigma $
-finite. Let
![]() $k_n$
be the equidistribution on
$k_n$
be the equidistribution on
![]() $C_n$
and let
$C_n$
and let
![]() $\nu _n(f)=\prod _{k=1}^n\kappa _k(1_G)$
for each
$\nu _n(f)=\prod _{k=1}^n\kappa _k(1_G)$
for each
![]() $f\in F_n$
and
$f\in F_n$
and
![]() $n\ge 0$
. Then, equations (2.2) and (2.3) hold for
$n\ge 0$
. Then, equations (2.2) and (2.3) hold for
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
. Of course, the Haar measure for
$(\nu _n)_{n=0}^\infty $
. Of course, the Haar measure for
![]() $\mathcal R$
is a
$\mathcal R$
is a
![]() $(C,F)$
-measure determined by
$(C,F)$
-measure determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
. The Haar measure is finite if and only if
$(\nu _n)_{n=0}^\infty $
. The Haar measure is finite if and only if
 $$ \begin{align*} \prod_{n=1}^\infty\frac{\# F_{n+1}}{\# F_n\# C_{n+1}}<\infty. \end{align*} $$
$$ \begin{align*} \prod_{n=1}^\infty\frac{\# F_{n+1}}{\# F_n\# C_{n+1}}<\infty. \end{align*} $$
It is easy to verify that
![]() $\mathcal R$
is conservative and ergodic on the
$\mathcal R$
is conservative and ergodic on the
![]() $\sigma $
-finite measure space
$\sigma $
-finite measure space
![]() $(X,\mu )$
. This means that for each
$(X,\mu )$
. This means that for each
![]() $\mathcal R$
-invariant subset
$\mathcal R$
-invariant subset
![]() $A\subset X$
, either
$A\subset X$
, either
![]() $\mu (A)=0$
or
$\mu (A)=0$
or
![]() $\mu (X\setminus A)=0$
.
$\mu (X\setminus A)=0$
.
Since the set of quasi-invariant probability measures with a fixed Radon–Nikodym derivative is a simplex [Reference Greschonig and SchmidtGrSc], it makes sense to introduce the following definition.
Definition 2.6. Let
![]() $\mathcal S$
be a Borel countable equivalence relation on a locally compact Polish space Z. Given a Borel cocycle
$\mathcal S$
be a Borel countable equivalence relation on a locally compact Polish space Z. Given a Borel cocycle
![]() $\rho :\mathcal S\to \mathbb R^*_+$
, we say that
$\rho :\mathcal S\to \mathbb R^*_+$
, we say that
![]() $\mathcal S$
is Radon
$\mathcal S$
is Radon
![]() $\rho $
-uniquely ergodic if there is a unique (up to scaling) Radon
$\rho $
-uniquely ergodic if there is a unique (up to scaling) Radon
![]() $\mathcal S$
-quasi-invariant measure
$\mathcal S$
-quasi-invariant measure
![]() $\unicode{x3bb} $
on Z such that
$\unicode{x3bb} $
on Z such that
![]() $\rho _\unicode{x3bb} =\rho $
.
$\rho _\unicode{x3bb} =\rho $
.
Proposition 2.7. Let
![]() $\mu $
be a
$\mu $
be a
![]() $(C,F)$
-measure on X determined by two sequences
$(C,F)$
-measure on X determined by two sequences
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
of finite measures satisfying equations (2.2) and (2.3). Then,
$(\nu _n)_{n=0}^\infty $
of finite measures satisfying equations (2.2) and (2.3). Then,
![]() $\mathcal R$
is Radon
$\mathcal R$
is Radon
![]() $\rho _\mu $
-uniquely ergodic.
$\rho _\mu $
-uniquely ergodic.
Proof. Let
![]() $\unicode{x3bb} $
be a Radon measure on X such that
$\unicode{x3bb} $
be a Radon measure on X such that
![]() $\rho _\unicode{x3bb} =\rho _\mu $
and
$\rho _\unicode{x3bb} =\rho _\mu $
and
![]() $\unicode{x3bb} (X_0)=1$
. We will prove that
$\unicode{x3bb} (X_0)=1$
. We will prove that
![]() $\unicode{x3bb} =\mu $
. For that, it suffices to show that
$\unicode{x3bb} =\mu $
. For that, it suffices to show that
![]() $\unicode{x3bb} ([f]_n)=\mu ([f]_n)$
for all
$\unicode{x3bb} ([f]_n)=\mu ([f]_n)$
for all
![]() $f\in F_n$
and
$f\in F_n$
and
![]() $n\ge 0$
. As
$n\ge 0$
. As
it is enough to prove that
![]() $\mu ([1_G]_n)=\unicode{x3bb} ([1_G]_n)$
for each
$\mu ([1_G]_n)=\unicode{x3bb} ([1_G]_n)$
for each
![]() $n\ge 0$
. This will be done inductively. Of course,
$n\ge 0$
. This will be done inductively. Of course,
![]() $\mu (X_0)=\mu ([1_G]_0)=\unicode{x3bb} ([1_G]_0)=\unicode{x3bb} (X_0)=1$
. Suppose that
$\mu (X_0)=\mu ([1_G]_0)=\unicode{x3bb} ([1_G]_0)=\unicode{x3bb} (X_0)=1$
. Suppose that
![]() $\mu ([1_G]_n)=\unicode{x3bb} ([1_G]_n)$
for some n. Then, for each
$\mu ([1_G]_n)=\unicode{x3bb} ([1_G]_n)$
for some n. Then, for each
![]() $c\in C_{n+1}$
,
$c\in C_{n+1}$
,
Since
![]() $[1_G]_n=\bigsqcup _{c\in C_{n+1}}[c]_{n+1}$
, we obtain that
$[1_G]_n=\bigsqcup _{c\in C_{n+1}}[c]_{n+1}$
, we obtain that
 $$ \begin{align*} \frac{\unicode{x3bb}([1_G]_{n})}{\unicode{x3bb}([1_G]_{n+1})} =\frac{\sum_{c\in C_{n+1}}\unicode{x3bb}([c]_{n+1})}{\unicode{x3bb}([1_G]_{n+1})} =\frac{\sum_{c\in C_{n+1}}\kappa_{n+1}(c)}{\kappa_{n+1}(1_G)} =\frac{1}{\kappa_{n+1}(1_G)} =\frac{\mu([1_G]_n)}{\mu([1_G]_{n+1})}. \end{align*} $$
$$ \begin{align*} \frac{\unicode{x3bb}([1_G]_{n})}{\unicode{x3bb}([1_G]_{n+1})} =\frac{\sum_{c\in C_{n+1}}\unicode{x3bb}([c]_{n+1})}{\unicode{x3bb}([1_G]_{n+1})} =\frac{\sum_{c\in C_{n+1}}\kappa_{n+1}(c)}{\kappa_{n+1}(1_G)} =\frac{1}{\kappa_{n+1}(1_G)} =\frac{\mu([1_G]_n)}{\mu([1_G]_{n+1})}. \end{align*} $$
Hence,
![]() $\unicode{x3bb} ([1_G]_{n+1})=\mu ([1_G]_{n+1})$
, as desired.
$\unicode{x3bb} ([1_G]_{n+1})=\mu ([1_G]_{n+1})$
, as desired.
2.3. Non-singular
 $(C,F)$
-actions
$(C,F)$
-actions
Non-singular
![]() $(C,F)$
-actions were defined in [Reference DanilenkoDa1, Reference DanilenkoDa2] for Abelian groups only. We extend this definition to arbitrary countable groups. Given
$(C,F)$
-actions were defined in [Reference DanilenkoDa1, Reference DanilenkoDa2] for Abelian groups only. We extend this definition to arbitrary countable groups. Given
![]() $g\in G$
, let
$g\in G$
, let
Then,
![]() $X_n^g$
is a compact open subset of
$X_n^g$
is a compact open subset of
![]() $X_n$
and
$X_n$
and
![]() $X_n^g\subset X^g_{n+1}$
. Hence, the union
$X_n^g\subset X^g_{n+1}$
. Hence, the union
![]() ${X^g:=\bigcup _{n\ge 0}X_n^g}$
is an open subset of X. Let
${X^g:=\bigcup _{n\ge 0}X_n^g}$
is an open subset of X. Let
![]() $X^G:=\bigcap _{g\in G}X^g$
. Then,
$X^G:=\bigcap _{g\in G}X^g$
. Then,
![]() $X^G$
is a
$X^G$
is a
![]() $G_\delta $
-subset of X. Hence,
$G_\delta $
-subset of X. Hence,
![]() $X^G$
is Polish and totally disconnected in the induced topology. Given
$X^G$
is Polish and totally disconnected in the induced topology. Given
![]() $g\in G$
and
$g\in G$
and
![]() $x\in X_G$
, there is
$x\in X_G$
, there is
![]() $n>0$
such that
$n>0$
such that
![]() $x= (f_n, c_{n+1},\ldots )\in X_n$
and
$x= (f_n, c_{n+1},\ldots )\in X_n$
and
![]() $gf_n\in F_n$
. We now let
$gf_n\in F_n$
. We now let
![]() $T_gx:= (gf_n, c_{n+1}, \ldots )\in X_n\subset X$
. It is straightforward to verify that:
$T_gx:= (gf_n, c_{n+1}, \ldots )\in X_n\subset X$
. It is straightforward to verify that:
-
(i)
 $T_gx\in X^G$
;
$T_gx\in X^G$
; -
(ii) the mapping
 $T_g:X^G\ni x\mapsto T_gx\in X^G$
is a homeomorphism of
$T_g:X^G\ni x\mapsto T_gx\in X^G$
is a homeomorphism of
 $X^G$
; and
$X^G$
; and -
(iii)
 $T_gT_{g'}=T_{gg'}$
for all
$T_gT_{g'}=T_{gg'}$
for all
 $g, g'\in G$
.
$g, g'\in G$
.
Hence,
![]() $T:=(T_g)_{g\in G}$
is a continuous G-action on
$T:=(T_g)_{g\in G}$
is a continuous G-action on
![]() $X^G$
.
$X^G$
.
Definition 2.8. [Reference DanilenkoDa3]
The action T is called the topological
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $(C_n,F_{n-1})_{n=1}^\infty $
.
$(C_n,F_{n-1})_{n=1}^\infty $
.
This action is free. The subset
![]() $X^G$
is
$X^G$
is
![]() $\mathcal R$
-invariant. The T-orbit equivalence relation coincides with the restriction of
$\mathcal R$
-invariant. The T-orbit equivalence relation coincides with the restriction of
![]() $\mathcal R$
to
$\mathcal R$
to
![]() $X^G$
.
$X^G$
.
Proposition 2.9. [Reference DanilenkoDa3, Proposition 1.2]
![]() $X^G=X$
if and only if for each
$X^G=X$
if and only if for each
![]() $g\in G$
and
$g\in G$
and
![]() $n>0$
, there is
$n>0$
, there is
![]() $m> n$
such that
$m> n$
such that
Thus, if equation (2.4) holds, then T is a minimal continuous G-action on a locally compact Cantor space X. Moreover, T is Radon uniquely ergodic, that is, there exists a unique T-invariant Radon measure
![]() $\xi $
on X such that
$\xi $
on X such that
![]() $\xi (X_0)=1$
.
$\xi (X_0)=1$
.
From now on, T is a topological
![]() $(C,F)$
-action of G on
$(C,F)$
-action of G on
![]() $X^G$
and
$X^G$
and
![]() $\mu $
is the non-singular
$\mu $
is the non-singular
![]() $(C,F)$
-measure on X determined by
$(C,F)$
-measure on X determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
satisfying equations (2.2) and (2.3). Since
$(\nu _n)_{n=0}^\infty $
satisfying equations (2.2) and (2.3). Since
![]() $X^G$
is
$X^G$
is
![]() $\mathcal R$
-invariant, we obtain that either
$\mathcal R$
-invariant, we obtain that either
![]() $\mu (X^G)=0$
or
$\mu (X^G)=0$
or
![]() $\mu (X\setminus X^G)=0$
. In the latter case, T is
$\mu (X\setminus X^G)=0$
. In the latter case, T is
![]() $\mu $
-non-singular, conservative and ergodic.
$\mu $
-non-singular, conservative and ergodic.
Proposition 2.10. The following are equivalent.
-
(i)
 $\mu (X\setminus X^G)=0$
.
$\mu (X\setminus X^G)=0$
. -
(ii) For each
 $g\in G$
and every
$g\in G$
and every
 $n \ge 0$
,
$n \ge 0$
, 
-
(iii) For each
 $g\in G$
,
$g\in G$
, 
Proof. (i)
![]() $\Leftrightarrow $
(ii) Since
$\Leftrightarrow $
(ii) Since
![]() $\mu (X\setminus X^G)=0$
if and only if
$\mu (X\setminus X^G)=0$
if and only if
![]() $ \mu (X_n\cap X^g_m)\to \mu (X_n)$
as
$ \mu (X_n\cap X^g_m)\to \mu (X_n)$
as
![]() $m\to \infty $
for each
$m\to \infty $
for each
![]() $g\in G$
and
$g\in G$
and
![]() $n \ge 0$
, it suffices to note that
$n \ge 0$
, it suffices to note that

and
![]() $\mu (X_n)=\mu ([F_n]_n)=\nu _n(F_n)$
.
$\mu (X_n)=\mu ([F_n]_n)=\nu _n(F_n)$
.
(ii)
![]() $\Rightarrow $
(iii) We set
$\Rightarrow $
(iii) We set ![]() . Then,
. Then,

Hence, ![]() according to item (ii). As
according to item (ii). As
![]() $\kappa _{1,m}$
is supported on
$\kappa _{1,m}$
is supported on ![]() , it follows that
, it follows that

as desired.
(iii)
![]() $\Rightarrow $
(i) Fix
$\Rightarrow $
(i) Fix
![]() $g\in G$
. Take arbitrary
$g\in G$
. Take arbitrary
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $f\in F_n$
. Then, it follows from property (iii) that for
$f\in F_n$
. Then, it follows from property (iii) that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x= (1_G, c_{n+1}, c_{n+2},\ldots)\in [1_G]_n$
, there exists
$x= (1_G, c_{n+1}, c_{n+2},\ldots)\in [1_G]_n$
, there exists
![]() $m>0$
such that
$m>0$
such that ![]() . This means that for
. This means that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $y= (f_n, c_{n+1}, c_{n+2},\ldots )\in X_n$
,
$y= (f_n, c_{n+1}, c_{n+2},\ldots )\in X_n$
,
that is,
![]() $y\in X^g$
. Hence,
$y\in X^g$
. Hence,
![]() $\mu (X\setminus X^g)=0$
and property (i) follows.
$\mu (X\setminus X^g)=0$
and property (i) follows.
In the case where
![]() $\mu $
is the Haar measure for
$\mu $
is the Haar measure for
![]() $\mathcal R$
, the equivalence (i)
$\mathcal R$
, the equivalence (i)
![]() $\Leftrightarrow $
(ii) of Proposition 2.10 was proved in [Reference DanilenkoDa3].
$\Leftrightarrow $
(ii) of Proposition 2.10 was proved in [Reference DanilenkoDa3].
Corollary 2.11.
-
(i) If
 $\mu (X\setminus X^G)=0$
and
$\mu (X\setminus X^G)=0$
and
 $\mu (X)<\infty $
, then
$\mu (X)<\infty $
, then
 $\nu _n(F_n\triangle gF_n)\to 0$
as
$\nu _n(F_n\triangle gF_n)\to 0$
as
 $n\to \infty $
for each
$n\to \infty $
for each
 $g\in G$
.
$g\in G$
. -
(ii) If
 $\mu (X\setminus X^G)=0$
,
$\mu (X\setminus X^G)=0$
,
 $\mu (X)<\infty $
and
$\mu (X)<\infty $
and
 $\mu $
is the Haar measure for
$\mu $
is the Haar measure for
 $\mathcal R$
, then G is amenable and
$\mathcal R$
, then G is amenable and
 $(F_n)_{n=1}^\infty $
is a left Følner sequence in G.
$(F_n)_{n=1}^\infty $
is a left Følner sequence in G. -
(iii) If
 $\mu (X\setminus X^G)=0$
,
$\mu (X\setminus X^G)=0$
,
 $\mu (X)<\infty $
,
$\mu (X)<\infty $
,
 $\mu $
is the Haar measure for
$\mu $
is the Haar measure for
 $\mathcal R$
and there exists a subgroup H of G such that
$\mathcal R$
and there exists a subgroup H of G such that
 $C_n\subset H$
eventually in n, then H is of finite index in G.
$C_n\subset H$
eventually in n, then H is of finite index in G.
Proof. (i) We note that
![]() $\nu _n(F_n)=\mu ([F_n]_n)=\mu (X_n)\to \mu (X)$
as
$\nu _n(F_n)=\mu ([F_n]_n)=\mu (X_n)\to \mu (X)$
as
![]() $n\to \infty $
. Hence, it follows from Proposition 2.10(ii) that for each
$n\to \infty $
. Hence, it follows from Proposition 2.10(ii) that for each
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $n>0$
such that if
$n>0$
such that if
![]() $m>n$
, then
$m>n$
, then

Hence,
![]() $\nu _m(F_m\cap gF_m)>(1-2\epsilon )\nu _m(F_m)$
. It follows that
$\nu _m(F_m\cap gF_m)>(1-2\epsilon )\nu _m(F_m)$
. It follows that
![]() $\lim _{m\to \infty }\nu _m(F_m\triangle gF_m)=0$
, as desired.
$\lim _{m\to \infty }\nu _m(F_m\triangle gF_m)=0$
, as desired.
(ii) Since
![]() $\mu $
is the Haar measure for
$\mu $
is the Haar measure for
![]() $\mathcal R$
, it follows that
$\mathcal R$
, it follows that ![]() for each subset
for each subset
![]() $A\subset F_n$
. Since
$A\subset F_n$
. Since
![]() $\mu $
is finite, there exists a limit
$\mu $
is finite, there exists a limit
This fact and condition (i) yield that for each
![]() $g\in G$
,
$g\in G$
,
Hence,
![]() $(F_n)_{n=1}^\infty $
is a left Følner sequence in G. Therefore, G is amenable.
$(F_n)_{n=1}^\infty $
is a left Følner sequence in G. Therefore, G is amenable.
(iii) Suppose that H is of infinite index in G. We first prove an auxiliary claim.
Claim A. For each finite subset
![]() $S\subset G$
, there exists an element
$S\subset G$
, there exists an element
![]() $g\in G$
such that
$g\in G$
such that
![]() $g\not \in \bigcup _{a,b\in S}aHb^{-1}$
.
$g\not \in \bigcup _{a,b\in S}aHb^{-1}$
.
By condition (ii), G is amenable. Hence, there exists a left-invariant finitely additive measure
![]() $\xi $
on the
$\xi $
on the
![]() $\sigma $
-algebra of all subsets of G such that
$\sigma $
-algebra of all subsets of G such that
![]() $\xi (G)=1$
. We first observe that since H is of infinite index,
$\xi (G)=1$
. We first observe that since H is of infinite index,
![]() $\xi (H)=0$
. Indeed, for each
$\xi (H)=0$
. Indeed, for each
![]() $n>0$
, there are elements
$n>0$
, there are elements
![]() $g_1,\ldots ,g_n\in G$
such that the cosets
$g_1,\ldots ,g_n\in G$
such that the cosets
![]() $g_1H,\ldots ,g_nH$
are mutually disjoint. Hence,
$g_1H,\ldots ,g_nH$
are mutually disjoint. Hence,
 $$ \begin{align*} 1\ge \xi\bigg(\bigsqcup_{j=1}^ng_jH\bigg)=\sum_{j=1}^n\xi(g_jH)=\sum_{j=1}^n\xi(H)=n\xi(H). \end{align*} $$
$$ \begin{align*} 1\ge \xi\bigg(\bigsqcup_{j=1}^ng_jH\bigg)=\sum_{j=1}^n\xi(g_jH)=\sum_{j=1}^n\xi(H)=n\xi(H). \end{align*} $$
This yields that
![]() $\xi (H)=0$
, as desired. As
$\xi (H)=0$
, as desired. As
![]() $g^{-1}Hg$
is also a subgroup of infinite index in G, it follows that
$g^{-1}Hg$
is also a subgroup of infinite index in G, it follows that
![]() $\xi (g^{-1}Hg)=0$
for each
$\xi (g^{-1}Hg)=0$
for each
![]() $g\in G$
. Since
$g\in G$
. Since
![]() $\xi $
is left-invariant,
$\xi $
is left-invariant,
![]() $\xi (kHg)=0$
for all
$\xi (kHg)=0$
for all
![]() $k,g\in G$
. This implies that
$k,g\in G$
. This implies that
![]() $ \xi (\bigcup _{a,b\in S}aHb^{-1})=0. $
Therefore,
$ \xi (\bigcup _{a,b\in S}aHb^{-1})=0. $
Therefore,
![]() $G\ne \bigcup _{a,b\in S}aHb^{-1}$
. Thus, Claim A is proved.
$G\ne \bigcup _{a,b\in S}aHb^{-1}$
. Thus, Claim A is proved.
Since
![]() $\mu (X)<\infty $
, there exists n such that
$\mu (X)<\infty $
, there exists n such that
![]() $\nu _n(F_n)>0.5\nu _m(F_m)$
and
$\nu _n(F_n)>0.5\nu _m(F_m)$
and
![]() $C_m\subset H$
for each
$C_m\subset H$
for each
![]() $m\ge n$
. Hence,
$m\ge n$
. Hence,
for each
![]() $m\ge n$
. By Claim A, there is
$m\ge n$
. By Claim A, there is
![]() $g\in G$
such that
$g\in G$
such that
![]() $gF_nH\cap F_nH=\emptyset $
. Since
$gF_nH\cap F_nH=\emptyset $
. Since
![]() $\mu $
is the Haar measure, it follows that
$\mu $
is the Haar measure, it follows that

This inequality and condition (i) yield that
![]() $\nu _m ((gF_nH)\cap F_m)>0.5\nu _m(F_m)$
eventually in m. Therefore,
$\nu _m ((gF_nH)\cap F_m)>0.5\nu _m(F_m)$
eventually in m. Therefore,
![]() $\nu _m(F_nH\cap gF_nH)>0$
eventually in m, which is a contradiction.
$\nu _m(F_nH\cap gF_nH)>0$
eventually in m, which is a contradiction.
Definition 2.12. If
![]() $\mu (X\setminus X^G)=0$
, then the dynamical system
$\mu (X\setminus X^G)=0$
, then the dynamical system
![]() $(X,\mu , T)$
(or simply T) is called the non-singular
$(X,\mu , T)$
(or simply T) is called the non-singular
![]() $(C,F)$
-action associated with
$(C,F)$
-action associated with
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
.
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
.
From now on, we consider only the case where
![]() $\mu (X\setminus X^G)=0$
. As
$\mu (X\setminus X^G)=0$
. As
![]() $X=X^G$
mod 0, we will assume that T is defined on the entire space X. Then for each n and every two elements
$X=X^G$
mod 0, we will assume that T is defined on the entire space X. Then for each n and every two elements
![]() $g,h\in F_n$
, we have that
$g,h\in F_n$
, we have that
![]() $T_{hg^{-1}}[g]_n=[h]_n$
and the Radon–Nikodym derivative of the transformation
$T_{hg^{-1}}[g]_n=[h]_n$
and the Radon–Nikodym derivative of the transformation
![]() $T_{hg^{-1}}$
is constant on the subset
$T_{hg^{-1}}$
is constant on the subset
![]() $[g]_n$
. More precisely, this constant equals
$[g]_n$
. More precisely, this constant equals
![]() ${\nu _n(h)}/{\nu _n(g)}$
.
${\nu _n(h)}/{\nu _n(g)}$
.
We now prove the main result of this section.
Theorem 2.13. Each non-singular
![]() $(C,F)$
-action is of rank one. Conversely, each rank-one non-singular G-action is isomorphic (via a measure preserving isomorphism) to a
$(C,F)$
-action is of rank one. Conversely, each rank-one non-singular G-action is isomorphic (via a measure preserving isomorphism) to a
![]() $(C,F)$
-action.
$(C,F)$
-action.
Proof. Let a sequence
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). We claim that the
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). We claim that the
![]() $(C,F)$
-action
$(C,F)$
-action
![]() $T=(T_g)_{g\in G}$
associated with this sequence is of rank one along
$T=(T_g)_{g\in G}$
associated with this sequence is of rank one along
![]() $(F_n)_{n=0}^\infty $
. Let X be the space of this action and let
$(F_n)_{n=0}^\infty $
. Let X be the space of this action and let
![]() $\mu $
be the
$\mu $
be the
![]() $(C,F)$
-measure on X determined by
$(C,F)$
-measure on X determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
. Then,
$(\nu _n)_{n=0}^\infty $
. Then,
![]() $X=\bigcup _{n\ge 0}X_n$
and
$X=\bigcup _{n\ge 0}X_n$
and
![]() $\mathcal R=\bigcup _{n\ge 1}\mathcal S_n$
, where
$\mathcal R=\bigcup _{n\ge 1}\mathcal S_n$
, where
![]() $X_n$
and
$X_n$
and
![]() $\mathcal S_n$
were introduced in §2.2. Of course, for each
$\mathcal S_n$
were introduced in §2.2. Of course, for each
![]() $n\in \mathbb N$
, the pair
$n\in \mathbb N$
, the pair
![]() $([1_G]_n,F_n)$
is a Rokhlin tower for T. Moreover:
$([1_G]_n,F_n)$
is a Rokhlin tower for T. Moreover:
-
(a)
 $X_{[1_G]_n,F_n}=X_n$
;
$X_{[1_G]_n,F_n}=X_n$
; -
(b)
 $\xi _{[1_G]_n,F_n}$
is the partition of
$\xi _{[1_G]_n,F_n}$
is the partition of
 $X_n$
into cylinders
$X_n$
into cylinders
 $[f]_n$
,
$[f]_n$
,
 $f\in F_n$
; and
$f\in F_n$
; and -
(c) if
 $x=(f_n,c_{n+1},\ldots )\in X_n\cap X^G$
, then
$x=(f_n,c_{n+1},\ldots )\in X_n\cap X^G$
, then
 $O_{[1_G]_n,F_n}(x)=\{T_gx\mid g\in {F_nf_n^{-1}}\}=\mathcal S_n(x)$
.
$O_{[1_G]_n,F_n}(x)=\{T_gx\mid g\in {F_nf_n^{-1}}\}=\mathcal S_n(x)$
.
We note that items (a) and (b) imply that Definition 2.1(i) holds. It follows from Proposition 2.10 that for a.e.
![]() $x\in X$
(or, more precisely, for each
$x\in X$
(or, more precisely, for each
![]() $x\in X^G$
), the T-orbit of x equals
$x\in X^G$
), the T-orbit of x equals
![]() $\mathcal R(x)$
. As
$\mathcal R(x)$
. As
![]() $\mathcal R(x)=\bigcup _{n=1}^\infty \mathcal S_n(x)$
, it follows that item (c) implies condition (ii) from Definition 2.1. Hence, T is of rank one along
$\mathcal R(x)=\bigcup _{n=1}^\infty \mathcal S_n(x)$
, it follows that item (c) implies condition (ii) from Definition 2.1. Hence, T is of rank one along
![]() $(F_n)_{n=1}^\infty $
.
$(F_n)_{n=1}^\infty $
.
Conversely, suppose that T is a non-singular G-action of rank one along an increasing sequence
![]() $(Q_n)_{n=0}^\infty $
of finite subsets in G with
$(Q_n)_{n=0}^\infty $
of finite subsets in G with
![]() $Q_0=\{1_G\}$
. Let
$Q_0=\{1_G\}$
. Let
![]() $(B_n,Q_n)_{n=0}^\infty $
be the corresponding generating sequence of Rokhlin towers such that conditions (i) and (ii) of Definition 2.1 hold. We have to define a sequence
$(B_n,Q_n)_{n=0}^\infty $
be the corresponding generating sequence of Rokhlin towers such that conditions (i) and (ii) of Definition 2.1 hold. We have to define a sequence
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
, satisfying equations (2.1)–(2.3) and Proposition 2.10(ii) such that the associated
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
, satisfying equations (2.1)–(2.3) and Proposition 2.10(ii) such that the associated
![]() $(C,F)$
-action is isomorphic to T. We first set
$(C,F)$
-action is isomorphic to T. We first set
![]() $F_n:=Q_n$
for each
$F_n:=Q_n$
for each
![]() $n\ge 0$
. By Definition 2.1(i), for each
$n\ge 0$
. By Definition 2.1(i), for each
![]() $n\ge 0$
, there is a subset
$n\ge 0$
, there is a subset
![]() $R_{n+1}\subset Q_{n+1}$
such that
$R_{n+1}\subset Q_{n+1}$
such that
![]() $B_n=\bigsqcup _{f\in R_{n+1}}T_f B_{n+1}$
. Without loss of generality, we may assume that
$B_n=\bigsqcup _{f\in R_{n+1}}T_f B_{n+1}$
. Without loss of generality, we may assume that
![]() $1_G\in R_{n+1}$
. Indeed, if this is not the case, we replace
$1_G\in R_{n+1}$
. Indeed, if this is not the case, we replace
![]() $(B_{n+1},Q_{n+1})$
with another Rokhlin tower
$(B_{n+1},Q_{n+1})$
with another Rokhlin tower
![]() $(T_sB_{n+1}, Q_{n+1}s^{-1})$
for an element
$(T_sB_{n+1}, Q_{n+1}s^{-1})$
for an element
![]() ${s\in R_{n+1}}$
. Then,
${s\in R_{n+1}}$
. Then,
![]() $\xi _{B_{n+1},Q_{n+1}}=\xi _{T_sB_{n+1}, Q_{n+1}s^{-1}}$
and
$\xi _{B_{n+1},Q_{n+1}}=\xi _{T_sB_{n+1}, Q_{n+1}s^{-1}}$
and
![]() $O_{B_{n+1},Q_{n+1}}(x)= O_{T_sB_{n+1}, Q_{n+1}s^{-1}}(x)$
for each
$O_{B_{n+1},Q_{n+1}}(x)= O_{T_sB_{n+1}, Q_{n+1}s^{-1}}(x)$
for each
![]() $x\in X$
. Hence, such replacements will not affect conditions (i) and (ii) of Definition 2.1. We now set
$x\in X$
. Hence, such replacements will not affect conditions (i) and (ii) of Definition 2.1. We now set
![]() $C_{n+1}:=R_{n+1}$
. Thus, we defined the entire sequence
$C_{n+1}:=R_{n+1}$
. Thus, we defined the entire sequence
![]() $(C_n,F_{n-1})_{n\ge 1}$
. It is straightforward to verify that equation (2.1) holds. Let
$(C_n,F_{n-1})_{n\ge 1}$
. It is straightforward to verify that equation (2.1) holds. Let
![]() $\nu _0$
be the Dirac measure supported at
$\nu _0$
be the Dirac measure supported at
![]() $1_G$
. Next, for each
$1_G$
. Next, for each
![]() $n> 0$
and
$n> 0$
and
![]() $f\in F_n$
, we let
$f\in F_n$
, we let
![]() $\nu _n(f):=\mu (T_fB_n)$
. Thus, we obtain a non-degenerated measure
$\nu _n(f):=\mu (T_fB_n)$
. Thus, we obtain a non-degenerated measure
![]() $\nu _n$
on
$\nu _n$
on
![]() $F_n$
. Finally, we define a probability
$F_n$
. Finally, we define a probability
![]() $\kappa _{n+1}$
on
$\kappa _{n+1}$
on
![]() $C_{n+1}$
by setting
$C_{n+1}$
by setting
Thus, the entire sequence of measures
![]() $(\kappa _n,\nu _{n-1})_{n\ge 1}$
is defined. It follows from condition (iii) which is below Definition 2.1 that
$(\kappa _n,\nu _{n-1})_{n\ge 1}$
is defined. It follows from condition (iii) which is below Definition 2.1 that
that is equation (2.3) holds. We note that for each
![]() $n>0$
, the restrictions of
$n>0$
, the restrictions of
![]() $\xi _{B_n,Q_n}$
to the subset
$\xi _{B_n,Q_n}$
to the subset
![]() $X_{B_0,Q_0}=B_0$
is the finite partition of
$X_{B_0,Q_0}=B_0$
is the finite partition of
![]() $B_0$
into subsets
$B_0$
into subsets ![]() , where
, where
![]() $(c_1,\ldots ,c_n)$
runs the subset
$(c_1,\ldots ,c_n)$
runs the subset ![]() . As
. As
![]() $\xi _{B_n,Q_n}\restriction B_0$
converges to the partition into singletons, we obtain that
$\xi _{B_n,Q_n}\restriction B_0$
converges to the partition into singletons, we obtain that
Since ![]() equation (2.2) follows.
equation (2.2) follows.
Fix
![]() $n>0$
,
$n>0$
,
![]() $g\in G$
and
$g\in G$
and
![]() $\epsilon>0$
. It follows from Definition 2.1(ii) that there exists
$\epsilon>0$
. It follows from Definition 2.1(ii) that there exists
![]() $M>n$
such that for each
$M>n$
such that for each
![]() $m>M$
, there is a subset
$m>M$
, there is a subset
![]() $A\subset X_{B_n,Q_n}$
such that
$A\subset X_{B_n,Q_n}$
such that
![]() $\mu ( X_{B_n,Q_n}\setminus A)<\epsilon $
and
$\mu ( X_{B_n,Q_n}\setminus A)<\epsilon $
and
![]() $T_gx\in O_{B_m,Q_m}(x)$
for each
$T_gx\in O_{B_m,Q_m}(x)$
for each
![]() $x\in A$
. Hence, there exist
$x\in A$
. Hence, there exist
![]() $f_1,f_2\in Q_m$
such that
$f_1,f_2\in Q_m$
such that
![]() ${T_gx=T_{f_1f_2^{-1}}x}$
and
${T_gx=T_{f_1f_2^{-1}}x}$
and
![]() $T_{f_2^{-1}}x\in B_m$
. As T is free,
$T_{f_2^{-1}}x\in B_m$
. As T is free,
![]() $gf_2=f_1\in Q_m=F_m$
. It follows that
$gf_2=f_1\in Q_m=F_m$
. It follows that
![]() ${T_{gf_2}B_m=T_{f_1}B_m\subset X_{B_m,Q_m}}$
. Since
${T_{gf_2}B_m=T_{f_1}B_m\subset X_{B_m,Q_m}}$
. Since
![]() $T_{f_2}B_m\ni x$
and
$T_{f_2}B_m\ni x$
and
![]() $x\in X_{B_n,Q_n}$
, we obtain that
$x\in X_{B_n,Q_n}$
, we obtain that
![]() $T_{f_2}B_m\subset X_{B_n,Q_n}$
because
$T_{f_2}B_m\subset X_{B_n,Q_n}$
because
![]() $\xi _{B_m,Q_m}$
is finer than
$\xi _{B_m,Q_m}$
is finer than
![]() $\xi _{B_n,Q_n}$
. Thus, without loss of generality, we may assume that A is measurable with respect to the partition
$\xi _{B_n,Q_n}$
. Thus, without loss of generality, we may assume that A is measurable with respect to the partition
![]() $\xi _{B_m,Q_m}$
. Since
$\xi _{B_m,Q_m}$
. Since

it follows that
![]() $T_{f_2}B_m\subset X_{B_n,Q_n}$
if and only if
$T_{f_2}B_m\subset X_{B_n,Q_n}$
if and only if ![]() . Hence,
. Hence,
This implies Proposition 2.10(ii).
Thus,
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
, satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by R the non-singular
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
, satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by R the non-singular
![]() $(C,F)$
-action associated with
$(C,F)$
-action associated with
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Let
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Let
![]() $(Y,\nu )$
be the space of this action. The correspondence
$(Y,\nu )$
be the space of this action. The correspondence
gives rise to a Boolean measure preserving isomorphism of the underlying algebras of measurable subsets on X and Y. The Boolean isomorphism is generated by a certain pointwise measure preserving isomorphism
![]() $\theta $
of
$\theta $
of
![]() $(X,\mu )$
onto
$(X,\mu )$
onto
![]() $(Y,\nu )$
. We claim that
$(Y,\nu )$
. We claim that
![]() $\theta $
intertwines T with R. Indeed, take
$\theta $
intertwines T with R. Indeed, take
![]() $g\in G$
. As was shown above, for each
$g\in G$
. As was shown above, for each
![]() $n>0$
and
$n>0$
and
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $M>n$
such that for each
$M>n$
such that for each
![]() $m>M$
, there is a subset
$m>M$
, there is a subset
![]() $Q'\subset Q_m$
such that
$Q'\subset Q_m$
such that
![]() $\bigsqcup _{f\in Q'}T_fB_m\subset X_{B_n,Q_n}$
,
$\bigsqcup _{f\in Q'}T_fB_m\subset X_{B_n,Q_n}$
,
![]() $\mu (X_{B_n,Q_n}\setminus \bigsqcup _{f\in Q'}T_fB_m)<\epsilon $
and
$\mu (X_{B_n,Q_n}\setminus \bigsqcup _{f\in Q'}T_fB_m)<\epsilon $
and
![]() $gQ'\subset Q_m$
. Hence,
$gQ'\subset Q_m$
. Hence,
Passing to the limit as
![]() $\epsilon \to 0$
and using the fact that
$\epsilon \to 0$
and using the fact that
![]() $\nu \circ \theta =\mu $
, we obtain that
$\nu \circ \theta =\mu $
, we obtain that
![]() ${\theta (T_gx)=R_g\theta x}$
for a.e.
${\theta (T_gx)=R_g\theta x}$
for a.e.
![]() $x\in X_n$
. Since n is arbitrary,
$x\in X_n$
. Since n is arbitrary,
![]() $\theta T_g=R_g\theta $
, as claimed.
$\theta T_g=R_g\theta $
, as claimed.
Remark 2.14.
-
(a) Theorem 2.13 corrects [Reference DanilenkoDa3, Theorem 1.6], where the particular case of
 $\sigma $
-finite measure preserving rank-one actions was under consideration: the condition (ii) (see Definition 2.1) is missing in the definition of rank one in [Reference DanilenkoDa3]. However, this condition cannot be omitted: counterexamples of non-rank-one action satisfying condition (i) (and hence not satisfying condition (ii)) is provided in Examples 4.4–4.6 below.
$\sigma $
-finite measure preserving rank-one actions was under consideration: the condition (ii) (see Definition 2.1) is missing in the definition of rank one in [Reference DanilenkoDa3]. However, this condition cannot be omitted: counterexamples of non-rank-one action satisfying condition (i) (and hence not satisfying condition (ii)) is provided in Examples 4.4–4.6 below. -
(b) It is worth noting that the condition on the Radon–Nikodym derivatives in the definition of Rokhlin tower in §2.1 is important and cannot be omitted either. Indeed, the associated flow of each non-singular
 $(C,F)$
-system is AT in the sense of Connes and Woods [Reference Connes and WoodsCoWo] (see also [Reference HamachiHa]). In [Reference Dooley and HamachiDoHa], Dooley and Hamachi constructed explicitly a Markov non-singular odometer (
$(C,F)$
-system is AT in the sense of Connes and Woods [Reference Connes and WoodsCoWo] (see also [Reference HamachiHa]). In [Reference Dooley and HamachiDoHa], Dooley and Hamachi constructed explicitly a Markov non-singular odometer (
 ${\mathbb Z}$
-action) whose associated flow is non-AT. Hence, this Markov odometer is not isomorphic (if fact, it is not even orbit equivalent) to any rank-one non-singular
${\mathbb Z}$
-action) whose associated flow is non-AT. Hence, this Markov odometer is not isomorphic (if fact, it is not even orbit equivalent) to any rank-one non-singular
 ${\mathbb Z}$
-action. (We do not provide definitions of orbit equivalence, associated flow and AT-flow because we will not use it anywhere below in this paper. Instead, we refer the interested reader to the survey [Reference Danilenko, Silva and MeyersDaSi].) However, it is easy to see that this odometer satisfies a ‘relaxed version’ of Definition 2.1 in which we drop only the condition on the Radon–Nikodym derivatives.
${\mathbb Z}$
-action. (We do not provide definitions of orbit equivalence, associated flow and AT-flow because we will not use it anywhere below in this paper. Instead, we refer the interested reader to the survey [Reference Danilenko, Silva and MeyersDaSi].) However, it is easy to see that this odometer satisfies a ‘relaxed version’ of Definition 2.1 in which we drop only the condition on the Radon–Nikodym derivatives.
2.4. Telescopings and reductions
Let a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
![]() $T=(T_g)_{g\in G}$
the
$T=(T_g)_{g\in G}$
the
![]() $(C,F)$
-action of G on X associated with
$(C,F)$
-action of G on X associated with
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $\mu $
stand for the non-singular
$\mu $
stand for the non-singular
![]() $(C,F)$
-measure on X determined by
$(C,F)$
-measure on X determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
.
$(\nu _n)_{n=0}^\infty $
.
Given a strictly increasing infinite sequence of integers
![]() $\boldsymbol l=(l_n)_{n=0}^\infty $
such that
$\boldsymbol l=(l_n)_{n=0}^\infty $
such that
![]() $l_0=0$
, we let
$l_0=0$
, we let
for each
![]() $n\ge 0$
.
$n\ge 0$
.
Definition 2.15. We call the sequence
![]() $\widetilde {\mathcal T}:=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
the
$\widetilde {\mathcal T}:=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
the
![]() $\boldsymbol l$
-telescoping of
$\boldsymbol l$
-telescoping of
![]() $\mathcal T$
.
$\mathcal T$
.
It is easy to check that
![]() $\widetilde {\mathcal T}$
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Hence, a non-singular
$\widetilde {\mathcal T}$
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Hence, a non-singular
![]() $(C,F)$
-action
$(C,F)$
-action
![]() $\widetilde T=(\widetilde T_g)_{g\in G}$
of G associated with
$\widetilde T=(\widetilde T_g)_{g\in G}$
of G associated with
![]() $\widetilde {\mathcal T}$
is well defined. Let
$\widetilde {\mathcal T}$
is well defined. Let
![]() $\widetilde X$
denote the space of
$\widetilde X$
denote the space of
![]() $\widetilde T$
and let
$\widetilde T$
and let
![]() $\widetilde \mu $
denote the non-singular
$\widetilde \mu $
denote the non-singular
![]() $(C,F)$
-measure on
$(C,F)$
-measure on
![]() $\widetilde X$
determined by
$\widetilde X$
determined by
![]() $(\widetilde \kappa _n)_{n=1}^\infty $
and
$(\widetilde \kappa _n)_{n=1}^\infty $
and
![]() $(\widetilde \nu _n)_{n=0}^\infty $
. There is a canonical measure preserving isomorphism
$(\widetilde \nu _n)_{n=0}^\infty $
. There is a canonical measure preserving isomorphism
![]() $\iota _{\boldsymbol l}$
of
$\iota _{\boldsymbol l}$
of
![]() $(X,\mu )$
onto
$(X,\mu )$
onto
![]() $(\widetilde X,\widetilde \mu )$
that intertwines T with
$(\widetilde X,\widetilde \mu )$
that intertwines T with
![]() $\widetilde T$
. Indeed, if
$\widetilde T$
. Indeed, if
![]() $x\in X$
, then we select the smallest
$x\in X$
, then we select the smallest
![]() $n\ge 0$
such that
$n\ge 0$
such that
![]() $x=(f_{l_n},c_{l_n+1},c_{l_n+2},\ldots )\in X_{l_n}$
. Let
$x=(f_{l_n},c_{l_n+1},c_{l_n+2},\ldots )\in X_{l_n}$
. Let
where ![]() . It is a routine to verify that
. It is a routine to verify that
![]() $\iota _{\boldsymbol l}$
is a homeomorphism of X onto
$\iota _{\boldsymbol l}$
is a homeomorphism of X onto
![]() $\widetilde X$
such that
$\widetilde X$
such that
![]() $\iota _{\boldsymbol l} T_g=\widetilde T_g\iota _{\boldsymbol l}$
for each
$\iota _{\boldsymbol l} T_g=\widetilde T_g\iota _{\boldsymbol l}$
for each
![]() $g\in G$
, as desired.
$g\in G$
, as desired.
Let
![]() $\boldsymbol l=(l_n)_{n=0}^\infty $
and
$\boldsymbol l=(l_n)_{n=0}^\infty $
and
![]() $\boldsymbol m=(m_n)_{n=0}^\infty $
be two strictly increasing sequences of integers such that
$\boldsymbol m=(m_n)_{n=0}^\infty $
be two strictly increasing sequences of integers such that
![]() $l_0=m_0=0$
. If
$l_0=m_0=0$
. If
![]() $\widetilde {\mathcal T}$
is the
$\widetilde {\mathcal T}$
is the
![]() $\boldsymbol l$
-telescoping of
$\boldsymbol l$
-telescoping of
![]() ${\mathcal T}$
and
${\mathcal T}$
and
![]() $\mathcal S$
is the
$\mathcal S$
is the
![]() $\boldsymbol m$
-telescoping of
$\boldsymbol m$
-telescoping of
![]() $\widetilde {\mathcal T}$
, then
$\widetilde {\mathcal T}$
, then
![]() $\mathcal S$
is the
$\mathcal S$
is the
![]() $\boldsymbol l\circ \boldsymbol m$
-telescoping of
$\boldsymbol l\circ \boldsymbol m$
-telescoping of
![]() $\mathcal T$
, where
$\mathcal T$
, where
![]() $\boldsymbol l\circ \boldsymbol m:=(l_{m_n})_{n=1}^\infty $
and
$\boldsymbol l\circ \boldsymbol m:=(l_{m_n})_{n=1}^\infty $
and
![]() $\iota _{\boldsymbol m}\circ \iota _{\boldsymbol l}=\iota _{\boldsymbol l\circ \boldsymbol m}$
.
$\iota _{\boldsymbol m}\circ \iota _{\boldsymbol l}=\iota _{\boldsymbol l\circ \boldsymbol m}$
.
Given a sequence
![]() $\boldsymbol A=(A_n)_{n=1}^\infty $
of subsets
$\boldsymbol A=(A_n)_{n=1}^\infty $
of subsets
![]() $A_n\subset C_{n}$
such that
$A_n\subset C_{n}$
such that
![]() $1_G\in A_n$
for each
$1_G\in A_n$
for each
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $\sum _{n=1}^\infty (1- \kappa _n(A_n))<\infty $
, we let
$\sum _{n=1}^\infty (1- \kappa _n(A_n))<\infty $
, we let
Then,
![]() $ \kappa ^{\prime }_n$
is a non-degenerated probability on
$ \kappa ^{\prime }_n$
is a non-degenerated probability on
![]() $A_n$
for each
$A_n$
for each
![]() $n\in \mathbb N$
. We also define a measure
$n\in \mathbb N$
. We also define a measure
![]() $\nu _n'$
on
$\nu _n'$
on
![]() $F_n$
by setting
$F_n$
by setting

if
![]() $n>0$
and
$n>0$
and
![]() $\nu _0':=\nu _0$
. Let
$\nu _0':=\nu _0$
. Let
![]() $\mathcal T':=(A_n,F_{n-1},\kappa _n',\nu _{n-1}')_{n=1}^\infty $
.
$\mathcal T':=(A_n,F_{n-1},\kappa _n',\nu _{n-1}')_{n=1}^\infty $
.
Definition 2.16. We call
![]() $\mathcal T'$
an
$\mathcal T'$
an
![]() $\boldsymbol A$
-reduction of
$\boldsymbol A$
-reduction of
![]() $\mathcal T$
.
$\mathcal T$
.
It is easy to check that
![]() $\mathcal T'$
satisfies equations (2.1)–(2.3). We note that
$\mathcal T'$
satisfies equations (2.1)–(2.3). We note that

for each
![]() $g\in G$
. Passing to the limit and using Proposition 2.10(iii) for
$g\in G$
. Passing to the limit and using Proposition 2.10(iii) for
![]() $\mathcal T$
, we obtain that
$\mathcal T$
, we obtain that ![]() as
as
![]() $m\to \infty $
. In other words,
$m\to \infty $
. In other words,
that is, Proposition 2.10(iii) holds for
![]() $\mathcal T'$
. Hence, a non-singular
$\mathcal T'$
. Hence, a non-singular
![]() $(C,F)$
-action
$(C,F)$
-action
![]() $ {T'=(T_g')_{g\in G}}$
of G associated with
$ {T'=(T_g')_{g\in G}}$
of G associated with
![]() $\mathcal T'$
is well defined. Let
$\mathcal T'$
is well defined. Let
![]() $X'$
denote the space of
$X'$
denote the space of
![]() $T'$
and let
$T'$
and let
![]() $\mu '$
denote the non-singular
$\mu '$
denote the non-singular
![]() $(C,F)$
-measure on
$(C,F)$
-measure on
![]() $X'$
determined by
$X'$
determined by
![]() $(\kappa _n')_{n=1}^\infty $
and
$(\kappa _n')_{n=1}^\infty $
and
![]() $(\nu _n')_{n=0}^\infty $
.
$(\nu _n')_{n=0}^\infty $
.
Proposition 2.17. There is a canonical measure scaling isomorphism
![]() $\iota _{\boldsymbol A}$
of
$\iota _{\boldsymbol A}$
of
![]() $(X,\mu )$
onto
$(X,\mu )$
onto
![]() $(X',\mu ')$
that intertwines T with
$(X',\mu ')$
that intertwines T with
![]() $T'$
and
$T'$
and ![]() .
.
Proof. Indeed, fix
![]() $n\in \mathbb N$
. Since
$n\in \mathbb N$
. Since ![]() , it follows from the Borel–Cantelli lemma that for a.e.
, it follows from the Borel–Cantelli lemma that for a.e.
![]() $x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n$
, there is
$x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n$
, there is
![]() $N=N_x>n$
such that
$N=N_x>n$
such that
![]() $c_m\in A_m$
for each
$c_m\in A_m$
for each
![]() $m>N$
. We then let
$m>N$
. We then let
It is routine to verify that
![]() $\iota _{\boldsymbol A,n}:X_n\ni x\mapsto \iota _{\boldsymbol A,n}(x)\in X'$
is a well-defined non-singular mapping and
$\iota _{\boldsymbol A,n}:X_n\ni x\mapsto \iota _{\boldsymbol A,n}(x)\in X'$
is a well-defined non-singular mapping and

Moreover,
![]() $\iota _{\boldsymbol A,n+1}\restriction X_n=\iota _{\boldsymbol A,n}$
for each
$\iota _{\boldsymbol A,n+1}\restriction X_n=\iota _{\boldsymbol A,n}$
for each
![]() $n\in \mathbb N$
. Hence, a measurable mapping
$n\in \mathbb N$
. Hence, a measurable mapping
![]() $\iota _{\boldsymbol A}:X\to X'$
is well defined by the restrictions
$\iota _{\boldsymbol A}:X\to X'$
is well defined by the restrictions
![]() $\iota _{\boldsymbol A}\restriction X_n=\iota _{\boldsymbol A,n}$
for all
$\iota _{\boldsymbol A}\restriction X_n=\iota _{\boldsymbol A,n}$
for all
![]() $n\in \mathbb N$
. It is straightforward to verify that
$n\in \mathbb N$
. It is straightforward to verify that
![]() $\iota _{\boldsymbol A}$
is an isomorphism of
$\iota _{\boldsymbol A}$
is an isomorphism of
![]() $(X,\mu )$
onto
$(X,\mu )$
onto
![]() $(X',\mu ')$
with
$(X',\mu ')$
with ![]() and
and
![]() $\iota _{\boldsymbol A}T_g=T_g'\iota _{\boldsymbol A}$
for each
$\iota _{\boldsymbol A}T_g=T_g'\iota _{\boldsymbol A}$
for each
![]() $g\in G$
.
$g\in G$
.
2.5. Locally compact models for rank-one non-singular systems
Let Z be a locally compact Polish G-space. We remind that a Borel mapping
![]() $\rho :G\times Z\to \mathbb R^*_+$
is called a G-cocycle if
$\rho :G\times Z\to \mathbb R^*_+$
is called a G-cocycle if
The following definition is a dynamical analogue of Definition 2.6.
Definition 2.18. Fix a G-cocycle
![]() $\rho $
. We say that the G-action on Z is Radon
$\rho $
. We say that the G-action on Z is Radon
![]() $\rho $
-uniquely ergodic if there exists a unique (up to scaling) Radon G-quasi-invariant measure
$\rho $
-uniquely ergodic if there exists a unique (up to scaling) Radon G-quasi-invariant measure
![]() $\gamma $
on Z such that
$\gamma $
on Z such that
We now show that each rank-one non-singular action has a uniquely ergodic continuous realization on a locally compact Cantor space.
Theorem 2.19. Let a non-singular action R of G on a
![]() $\sigma $
-finite standard non-atomic measure space
$\sigma $
-finite standard non-atomic measure space
![]() $(Z,\eta )$
be of rank one along a sequence
$(Z,\eta )$
be of rank one along a sequence
![]() $(Q_n)_{n=1}^\infty $
. Then there exist:
$(Q_n)_{n=1}^\infty $
. Then there exist:
-
(i) a continuous, minimal, Radon uniquely ergodic G-action
 $T'=(T_g')_{g\in G}$
defined on a locally compact Cantor space
$T'=(T_g')_{g\in G}$
defined on a locally compact Cantor space
 $X'$
;
$X'$
; -
(ii) a
 $T'$
-quasi-invariant Radon measure
$T'$
-quasi-invariant Radon measure
 $\mu '$
on
$\mu '$
on
 $X'$
such that the Radon–Nikodym derivative
$X'$
such that the Radon–Nikodym derivative
 ${d\mu '\circ T_g'}/{d\mu '} : X'\to \mathbb R^*_+$
is continuous for each
${d\mu '\circ T_g'}/{d\mu '} : X'\to \mathbb R^*_+$
is continuous for each
 $g\in G$
;
$g\in G$
; -
(iii) a measure preserving Borel isomorphism of
 $(Z,\eta )$
onto
$(Z,\eta )$
onto
 $(X',\mu ')$
that intertwines R with
$(X',\mu ')$
that intertwines R with
 $T'$
;
$T'$
; -
(iv) a sequence
 $\mathcal T'=(C_n',F_{n-1}',\kappa _n',\nu _{n-1}')_{n=1}^\infty $
satisfying equations (2.1)–(2.4) such that
$\mathcal T'=(C_n',F_{n-1}',\kappa _n',\nu _{n-1}')_{n=1}^\infty $
satisfying equations (2.1)–(2.4) such that
 $(X',\mu ',T')$
is the
$(X',\mu ',T')$
is the
 $(C,F)$
-action associated with
$(C,F)$
-action associated with
 $\mathcal T'$
; and
$\mathcal T'$
; and -
(v) a sequence
 $(z_n)_{n=1}^\infty $
such that
$(z_n)_{n=1}^\infty $
such that
 $z_n\in Q_n$
for each n and
$z_n\in Q_n$
for each n and
 $(F_n')_{n=1}^\infty $
is a subsequence of
$(F_n')_{n=1}^\infty $
is a subsequence of
 $(z_n^{-1}Q_n)_{n=1}^\infty $
.
$(z_n^{-1}Q_n)_{n=1}^\infty $
.
Moreover,
![]() $T'$
is Radon
$T'$
is Radon
![]() $({d\mu '\circ T_g'}/{d\mu '})_{g\in G}$
-uniquely ergodic.
$({d\mu '\circ T_g'}/{d\mu '})_{g\in G}$
-uniquely ergodic.
Proof. By Theorem 2.13, there is a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii) such that the
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii) such that the
![]() $(C,F)$
-action T of G associated with
$(C,F)$
-action T of G associated with
![]() $\mathcal T$
is isomorphic to R via a measure preserving isomorphism. Denote by
$\mathcal T$
is isomorphic to R via a measure preserving isomorphism. Denote by
![]() $(X,\mu )$
the space of T. Let
$(X,\mu )$
the space of T. Let
![]() $G=\{g_j\mid j\in \mathbb N\}$
. It follows from Proposition 2.10(ii) that there are an increasing sequence
$G=\{g_j\mid j\in \mathbb N\}$
. It follows from Proposition 2.10(ii) that there are an increasing sequence
![]() $\boldsymbol l=(l_n)_{n=0}^\infty $
of integers and a sequence
$\boldsymbol l=(l_n)_{n=0}^\infty $
of integers and a sequence
![]() $(D_n)_{n=1}^\infty $
of subsets in G such that
$(D_n)_{n=1}^\infty $
of subsets in G such that
![]() $l_0=0$
,
$l_0=0$
, ![]() and
and
for each
![]() $n\ge 0$
. Denote by
$n\ge 0$
. Denote by
![]() $\widetilde { \mathcal T}=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
the
$\widetilde { \mathcal T}=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
the
![]() $\boldsymbol l$
-telescoping of
$\boldsymbol l$
-telescoping of
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $(\widetilde X,\widetilde \mu , \widetilde T)$
stand for the
$(\widetilde X,\widetilde \mu , \widetilde T)$
stand for the
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\widetilde { \mathcal T}$
. Then,
$\widetilde { \mathcal T}$
. Then,
![]() $D_n\subset \widetilde C_n$
and
$D_n\subset \widetilde C_n$
and
![]() $\widetilde \kappa _n(D_n)>1-n^{-2}$
for each
$\widetilde \kappa _n(D_n)>1-n^{-2}$
for each
![]() $n>0$
. Denote by
$n>0$
. Denote by
![]() $\iota _{\boldsymbol l}$
the canonical measure preserving isomorphism intertwining T with
$\iota _{\boldsymbol l}$
the canonical measure preserving isomorphism intertwining T with
![]() $\widetilde T$
. In general,
$\widetilde T$
. In general,
![]() $1_G\not \in D_n$
. Therefore, we need to modify the
$1_G\not \in D_n$
. Therefore, we need to modify the
![]() $(C,F)$
-parameters
$(C,F)$
-parameters
![]() $\widetilde {\mathcal T}$
. First, we choose, for each
$\widetilde {\mathcal T}$
. First, we choose, for each
![]() $n>0$
, an element
$n>0$
, an element
![]() $c_n\in D_n$
. Then, we let
$c_n\in D_n$
. Then, we let
![]() $z_0:=1_G$
and
$z_0:=1_G$
and ![]() for each
for each
![]() $n>0$
. Finally, we define a new sequence
$n>0$
. Finally, we define a new sequence
![]() $\widehat { \mathcal T}=(\widehat C_n,\widehat F_{n-1},\widehat \kappa _n,\widehat \nu _{n-1})_{n=1}^\infty $
by setting
$\widehat { \mathcal T}=(\widehat C_n,\widehat F_{n-1},\widehat \kappa _n,\widehat \nu _{n-1})_{n=1}^\infty $
by setting
![]() $\widehat \kappa _n$
is the image of
$\widehat \kappa _n$
is the image of
![]() $\kappa _n$
under the bijection
$\kappa _n$
under the bijection
![]() $\widetilde C_n\ni c\mapsto z_{n-1}cz_n^{-1}\in \widehat C_n $
and
$\widetilde C_n\ni c\mapsto z_{n-1}cz_n^{-1}\in \widehat C_n $
and
![]() $\widehat \nu _{n-1}$
is the image of
$\widehat \nu _{n-1}$
is the image of
![]() $\nu _{n-1}$
under the bijection
$\nu _{n-1}$
under the bijection
![]() $\widetilde F_{n-1}\ni f\mapsto fz_{n-1}^{-1}\in \widehat F_{n-1}$
. It is straightforward to verify that
$\widetilde F_{n-1}\ni f\mapsto fz_{n-1}^{-1}\in \widehat F_{n-1}$
. It is straightforward to verify that
![]() $\widehat { \mathcal T}$
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
$\widehat { \mathcal T}$
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
![]() $(\widehat X,\widehat \mu ,\widehat T)$
the
$(\widehat X,\widehat \mu ,\widehat T)$
the
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\widehat { \mathcal T}$
. Then there is a canonical continuous measure preserving isomorphism
$\widehat { \mathcal T}$
. Then there is a canonical continuous measure preserving isomorphism
![]() $\vartheta : (\widetilde X,\widetilde \mu )\to ( \widehat X,\widehat \mu )$
that intertwines
$\vartheta : (\widetilde X,\widetilde \mu )\to ( \widehat X,\widehat \mu )$
that intertwines
![]() $\widetilde T$
with
$\widetilde T$
with
![]() $\widehat T$
:
$\widehat T$
:
Let
![]() $\widehat D_n$
be the image of
$\widehat D_n$
be the image of
![]() $D_n$
under the bijection
$D_n$
under the bijection
![]() $\widetilde C_n\ni c\mapsto z_{n-1}cz_n^{-1}\in \widehat C_n$
. Then,
$\widetilde C_n\ni c\mapsto z_{n-1}cz_n^{-1}\in \widehat C_n$
. Then,
![]() $1\in \widehat D_n$
and
$1\in \widehat D_n$
and
![]() $\widehat \kappa _n(\widehat D_n)>1-n^{-2}$
for each
$\widehat \kappa _n(\widehat D_n)>1-n^{-2}$
for each
![]() $n\in \mathbb N$
. Hence,
$n\in \mathbb N$
. Hence,
![]() $\sum _{n=1}^\infty (1-\widehat \kappa _n(\widehat D_n))<\infty $
. We now set
$\sum _{n=1}^\infty (1-\widehat \kappa _n(\widehat D_n))<\infty $
. We now set
![]() $\boldsymbol D:=(D_n)_{n=1}^\infty $
. Denote by
$\boldsymbol D:=(D_n)_{n=1}^\infty $
. Denote by
![]() $\mathcal T'$
the
$\mathcal T'$
the
![]() $\boldsymbol D$
-reduction of
$\boldsymbol D$
-reduction of
![]() $\widehat { \mathcal T}$
. Then,
$\widehat { \mathcal T}$
. Then,
![]() $\mathcal T'$
satisfies not only equations (2.1)–(2.3) and Proposition 2.10(ii), but also equation (2.4). Let
$\mathcal T'$
satisfies not only equations (2.1)–(2.3) and Proposition 2.10(ii), but also equation (2.4). Let
![]() $( X',\mu ', T')$
denote the
$( X',\mu ', T')$
denote the
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\mathcal T'$
and let
$\mathcal T'$
and let
![]() $\iota _{\boldsymbol D}$
stand for the canonical measure scaling isomorphism of
$\iota _{\boldsymbol D}$
stand for the canonical measure scaling isomorphism of
![]() $(\widehat X,\widehat \mu )$
onto
$(\widehat X,\widehat \mu )$
onto
![]() $( X',\mu ')$
that intertwines
$( X',\mu ')$
that intertwines
![]() $\widehat T$
with
$\widehat T$
with
![]() $T'$
. Then,
$T'$
. Then,
![]() $\iota _{\boldsymbol D}\circ \vartheta \circ \iota _{\boldsymbol l}$
is a measure-scaling isomorphism of
$\iota _{\boldsymbol D}\circ \vartheta \circ \iota _{\boldsymbol l}$
is a measure-scaling isomorphism of
![]() $(X,\mu , T)$
onto
$(X,\mu , T)$
onto
![]() $(X',\mu ',T')$
. Replacing
$(X',\mu ',T')$
. Replacing
![]() $\mu '$
with
$\mu '$
with ![]() for an appropriate
for an appropriate
![]() $a>0$
, we obtain that
$a>0$
, we obtain that
![]() $\iota _{\boldsymbol D}\circ \vartheta \circ \iota _{\boldsymbol l}$
is measure preserving. It follows from Proposition 2.9 that
$\iota _{\boldsymbol D}\circ \vartheta \circ \iota _{\boldsymbol l}$
is measure preserving. It follows from Proposition 2.9 that
![]() $T'$
is a Radon uniquely ergodic minimal continuous action of G on the locally compact Polish space
$T'$
is a Radon uniquely ergodic minimal continuous action of G on the locally compact Polish space
![]() $X'$
. Thus, we proved conditions (i), (iii), (iv) and (v). The condition (ii) follows easily from equation (2.4) and the definition of
$X'$
. Thus, we proved conditions (i), (iii), (iv) and (v). The condition (ii) follows easily from equation (2.4) and the definition of
![]() $\mu '$
.
$\mu '$
.
The final claim of the theorem follows from condition (iv) and Proposition 2.7.
2.6. Non-singular
 ${\mathbb Z}$
-actions of rank one along intervals and
${\mathbb Z}$
-actions of rank one along intervals and
 $(C,F)$
-construction
$(C,F)$
-construction
Let
![]() $G={\mathbb Z}$
. Suppose that a sequence
$G={\mathbb Z}$
. Suppose that a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii), and there is a sequence
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii), and there is a sequence
![]() $(h_n)_{n=0}^\infty $
of positive integers such that
$(h_n)_{n=0}^\infty $
of positive integers such that
![]() $F_n=\{0,1,\ldots ,h_n-1\}$
. Denote by
$F_n=\{0,1,\ldots ,h_n-1\}$
. Denote by
![]() $(X,\mu ,T)$
the
$(X,\mu ,T)$
the
![]() $(C,F)$
-dynamical system associated with
$(C,F)$
-dynamical system associated with
![]() $\mathcal T$
.
$\mathcal T$
.
We now show how to obtain
![]() $(X,\mu ,T)$
via the classical inductive geometric cutting-and-stacking in the case of
$(X,\mu ,T)$
via the classical inductive geometric cutting-and-stacking in the case of
![]() ${\mathbb Z}$
-actions. On the initial step of the construction, we define a column
${\mathbb Z}$
-actions. On the initial step of the construction, we define a column
![]() $Y_0$
consisting of a single interval
$Y_0$
consisting of a single interval
![]() $[0,1)$
equipped with Lebesgue measure. Assume that at the nth step, we have a column
$[0,1)$
equipped with Lebesgue measure. Assume that at the nth step, we have a column
consisting of disjoint intervals
![]() $I(i,n) \subset \mathbb R$
such that
$I(i,n) \subset \mathbb R$
such that
![]() $\bigsqcup _{i=0}^{h_n-1} I(i,n) = [0,\nu _n(F_n))$
. Then we define a continuous nth column mapping
$\bigsqcup _{i=0}^{h_n-1} I(i,n) = [0,\nu _n(F_n))$
. Then we define a continuous nth column mapping
such that
![]() $T^{(n)}\restriction I(i,n)$
is the orientation preserving affine mapping of
$T^{(n)}\restriction I(i,n)$
is the orientation preserving affine mapping of
![]() $I(i,n)$
onto
$I(i,n)$
onto
![]() $I(i+1,n)$
for
$I(i+1,n)$
for
![]() $i=0,\ldots ,h_n-2$
. It is convenient to think of
$i=0,\ldots ,h_n-2$
. It is convenient to think of
![]() $I(i,n)$
as a level of
$I(i,n)$
as a level of
![]() $Y_n$
. The levels may be of different length, but they are parallel to each other and the ith level is above the jth level if
$Y_n$
. The levels may be of different length, but they are parallel to each other and the ith level is above the jth level if
![]() $i>j$
. The nth column mapping moves every level, except the highest one, one level up. By the move here, we mean the orientation preserving affine mapping. On the highest level,
$i>j$
. The nth column mapping moves every level, except the highest one, one level up. By the move here, we mean the orientation preserving affine mapping. On the highest level,
![]() $T^{(n)}$
is not defined.
$T^{(n)}$
is not defined.
On the
![]() $(n+1)$
th step of the construction, we first cut each
$(n+1)$
th step of the construction, we first cut each
![]() $I(i, n)$
into subintervals
$I(i, n)$
into subintervals
![]() $I(i+c, n+1)$
,
$I(i+c, n+1)$
,
![]() $c\in C_{n+1}$
, such that
$c\in C_{n+1}$
, such that
![]() $I(i+c, n+1)$
is from the left of
$I(i+c, n+1)$
is from the left of
![]() $I(i+c', n+1)$
whenever
$I(i+c', n+1)$
whenever
![]() $c<c'$
and
$c<c'$
and
Hence, we obtain that
![]() $\bigsqcup _{j\in F_n+C_{n+1}}I(j,n+1)=[0,\nu _{n}(F_n))$
. Next, we cut the interval
$\bigsqcup _{j\in F_n+C_{n+1}}I(j,n+1)=[0,\nu _{n}(F_n))$
. Next, we cut the interval
![]() $[\nu _{n}(F_n),\nu _{n+1}(F_{n+1}))$
into subintervals
$[\nu _{n}(F_n),\nu _{n+1}(F_{n+1}))$
into subintervals
![]() $I(j, n+1)$
,
$I(j, n+1)$
,
![]() $j\in F_{n+1}\setminus (F_n+C_{n+1})$
, such that the length of
$j\in F_{n+1}\setminus (F_n+C_{n+1})$
, such that the length of
![]() $I(j, n+1)$
is
$I(j, n+1)$
is
![]() $\nu _{n+1}(j)$
for each j. These new levels are called spacers. Thus, we obtain a new column
$\nu _{n+1}(j)$
for each j. These new levels are called spacers. Thus, we obtain a new column
![]() $Y_{n+1}=\{I(j,n+1) \mid j \in F_{n+1}\}$
with
$Y_{n+1}=\{I(j,n+1) \mid j \in F_{n+1}\}$
with
![]() $\bigsqcup _{i\in F_{n+1}} I(i,n+1) = [0,\nu _{n+1}(F_{n+1}))$
. If an element
$\bigsqcup _{i\in F_{n+1}} I(i,n+1) = [0,\nu _{n+1}(F_{n+1}))$
. If an element
![]() $c\in C_{n+1}$
is not maximal in
$c\in C_{n+1}$
is not maximal in
![]() $C_{n+1}$
, then we denote by
$C_{n+1}$
, then we denote by
![]() $c^+$
the least element of
$c^+$
the least element of
![]() $C_{n+1}$
that is greater than c. We define a spacer mapping
$C_{n+1}$
that is greater than c. We define a spacer mapping
![]() ${s_{n+1}:C_{n+1}\to {\mathbb Z}_+}$
by setting
${s_{n+1}:C_{n+1}\to {\mathbb Z}_+}$
by setting
 $$ \begin{align*} s_{n+1}(c):= \begin{cases} c^+-c-h_n &\text{if } c\ne \max C_{n+1},\\ h_{n+1}-c-h_n&\text{if } c= \max C_{n+1}. \end{cases} \end{align*} $$
$$ \begin{align*} s_{n+1}(c):= \begin{cases} c^+-c-h_n &\text{if } c\ne \max C_{n+1},\\ h_{n+1}-c-h_n&\text{if } c= \max C_{n+1}. \end{cases} \end{align*} $$
The subcolumn
![]() $Y_{n,c}:=\{I(i+c,n+1)\mid i\in F_n\}\subset Y_{n+1}$
is called the c-copy of
$Y_{n,c}:=\{I(i+c,n+1)\mid i\in F_n\}\subset Y_{n+1}$
is called the c-copy of
![]() $Y_n$
,
$Y_n$
,
![]() ${c\in C_{n+1}}$
. Thus,
${c\in C_{n+1}}$
. Thus,
![]() $Y_{n+1}$
consists of
$Y_{n+1}$
consists of
![]() $\# C_{n+1}$
copies of
$\# C_{n+1}$
copies of
![]() $Y_{n}$
, and spacers between them and above the highest copy of
$Y_{n}$
, and spacers between them and above the highest copy of
![]() $Y_n$
. More precisely, there are exactly
$Y_n$
. More precisely, there are exactly
![]() $s_{n+1}(c)$
spacers above the c-copy of
$s_{n+1}(c)$
spacers above the c-copy of
![]() $Y_n$
in
$Y_n$
in
![]() $Y_{n+1}$
. The
$Y_{n+1}$
. The
![]() $(n+1)$
th column mapping
$(n+1)$
th column mapping
is defined in a similar way as
![]() $T^{(n)}$
. Of course,
$T^{(n)}$
. Of course,
Passing to the limit as
![]() $n\to \infty $
, we obtain a well-defined non-singular (piecewise affine) transformation Q of the interval
$n\to \infty $
, we obtain a well-defined non-singular (piecewise affine) transformation Q of the interval
![]() $[0,\lim _{n\to \infty }\nu _n(F_n))\subset \mathbb R$
equipped with Lebesgue measure such that
$[0,\lim _{n\to \infty }\nu _n(F_n))\subset \mathbb R$
equipped with Lebesgue measure such that
It is possible that
![]() $\lim _{n\to \infty }\nu _n(F_n)=\infty $
and then T is defined on
$\lim _{n\to \infty }\nu _n(F_n)=\infty $
and then T is defined on
![]() $[0,+\infty )$
. Of course, this transformation (or, more precisely, the
$[0,+\infty )$
. Of course, this transformation (or, more precisely, the
![]() ${\mathbb Z}$
-action generated by Q) is isomorphic to
${\mathbb Z}$
-action generated by Q) is isomorphic to
![]() $(X,\mu , T)$
. The according non-singular isomorphism is generated by the following correspondence:
$(X,\mu , T)$
. The according non-singular isomorphism is generated by the following correspondence:
Without loss of generality, we may assume
![]() $s_n(\max C_n)=0$
for each
$s_n(\max C_n)=0$
for each
![]() $n>0$
(see, for instance, [Reference DanilenkoDa4]). This means that there are no spacers over the highest copy of
$n>0$
(see, for instance, [Reference DanilenkoDa4]). This means that there are no spacers over the highest copy of
![]() $Y_n$
in
$Y_n$
in
![]() $Y_{n+1}$
.
$Y_{n+1}$
.
2.7. Non-singular rank-one
 ${\mathbb Z}$
-actions as transformations built under function over non-singular odometer base
${\mathbb Z}$
-actions as transformations built under function over non-singular odometer base
Let
![]() $(X,\mu , T)$
be as in the previous subsection. We will assume that
$(X,\mu , T)$
be as in the previous subsection. We will assume that
![]() $\max F_{n+1}=\max F_n+\max C_{n+1}$
for each
$\max F_{n+1}=\max F_n+\max C_{n+1}$
for each
![]() $n\ge 0$
. In terms of the geometrical cutting-and-stacking (see §2.6), this means exactly that there are no spacers on the top of the
$n\ge 0$
. In terms of the geometrical cutting-and-stacking (see §2.6), this means exactly that there are no spacers on the top of the
![]() $(n\kern1.5pt{+}\kern1.5pt1)$
th column. We remind that
$(n\kern1.5pt{+}\kern1.5pt1)$
th column. We remind that ![]() ,
, ![]() and
and
for each
![]() $n>0$
and
$n>0$
and
![]() $c\in C_n$
such that
$c\in C_n$
such that
![]() $c\ne \max C_n$
. Denote by R the transformation induced by
$c\ne \max C_n$
. Denote by R the transformation induced by
![]() $T_1$
on
$T_1$
on
![]() $(X_0,\mu \restriction X_0)$
. Since
$(X_0,\mu \restriction X_0)$
. Since
![]() $T_1$
is conservative, R is a well-defined non-singular transformation of
$T_1$
is conservative, R is a well-defined non-singular transformation of
![]() $X_0$
. Take
$X_0$
. Take
![]() $x=(c_1,c_2,\ldots )\in X_0$
. Choose
$x=(c_1,c_2,\ldots )\in X_0$
. Choose
![]() $n\ge 0$
such that
$n\ge 0$
such that
![]() $c_i=\max C_i$
for each
$c_i=\max C_i$
for each
![]() $i=1,\ldots ,n$
and
$i=1,\ldots ,n$
and
![]() $c_{n+1}\ne \max C_{n+1}$
. It is straightforward to verify that
$c_{n+1}\ne \max C_{n+1}$
. It is straightforward to verify that
 $$ \begin{align*} Rx:= (\underbrace{0,\ldots,0}_{n\text{ times}}, c_{n+1}^+, c_{n+2}, c_{n+3}\ldots) \end{align*} $$
$$ \begin{align*} Rx:= (\underbrace{0,\ldots,0}_{n\text{ times}}, c_{n+1}^+, c_{n+2}, c_{n+3}\ldots) \end{align*} $$
Thus, R is a classical non-singular odometer of product type (see [Reference AaronsonAa, Reference Danilenko, Silva and MeyersDaSi] and references therein). Let
![]() $x^{\max }:=(\max C_1,\max C_2,\ldots )\in X_0$
. We now define a function
$x^{\max }:=(\max C_1,\max C_2,\ldots )\in X_0$
. We now define a function
![]() $\vartheta :X_0\setminus \{x^{\max }\}\to {\mathbb Z}_+$
by setting
$\vartheta :X_0\setminus \{x^{\max }\}\to {\mathbb Z}_+$
by setting
if
![]() $x=(c_1,c_2,\ldots )$
,
$x=(c_1,c_2,\ldots )$
,
![]() $c_i=\max C_i$
for
$c_i=\max C_i$
for
![]() $i=1,\ldots ,n-1$
and
$i=1,\ldots ,n-1$
and
![]() $c_n\ne \max C_n$
, where
$c_n\ne \max C_n$
, where
![]() $s_n$
is the spacer mapping (see §2.6). Of course,
$s_n$
is the spacer mapping (see §2.6). Of course,
![]() $\vartheta $
is continuous. Then
$\vartheta $
is continuous. Then
![]() $(X,\mu ,T_1)$
is isomorphic to the transformation
$(X,\mu ,T_1)$
is isomorphic to the transformation
![]() $R^\theta $
built under
$R^\theta $
built under
![]() $\vartheta $
over the base R. We do not provide a proof of this fact which is essentially folklore.
$\vartheta $
over the base R. We do not provide a proof of this fact which is essentially folklore.
3. Finite factors of non-singular
 $(C,F)$
-actions
$(C,F)$
-actions
Let a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii), and let
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii), and let
![]() $\lim _{n\to \infty }\nu _n(F_n)<\infty $
. Let
$\lim _{n\to \infty }\nu _n(F_n)<\infty $
. Let
![]() $\Gamma $
be a cofinite subgroup of G. We consider the left coset space
$\Gamma $
be a cofinite subgroup of G. We consider the left coset space
![]() $G/\Gamma $
as a homogeneous G-space on which G acts by left translations. It is obvious that for each coset
$G/\Gamma $
as a homogeneous G-space on which G acts by left translations. It is obvious that for each coset
![]() $g\Gamma \in G/\Gamma $
, the subgroup
$g\Gamma \in G/\Gamma $
, the subgroup
![]() $g\Gamma g^{-1}\subset G$
is the stabilizer of
$g\Gamma g^{-1}\subset G$
is the stabilizer of
![]() $g\Gamma $
in G.
$g\Gamma $
in G.
Definition 3.1. Given a coset
![]() $g\Gamma \in G/\Gamma $
, we say that
$g\Gamma \in G/\Gamma $
, we say that
![]() ${\mathcal T}$
is compatible with
${\mathcal T}$
is compatible with
![]() $g\Gamma $
if
$g\Gamma $
if
 $$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g\Gamma g^{-1}\}) <\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g\Gamma g^{-1}\}) <\infty. \end{align*} $$
Denote by
![]() $(X,\mu ,T)$
the
$(X,\mu ,T)$
the
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\mathcal T$
. Then,
$\mathcal T$
. Then,
![]() $\mu (X)=\lim _{n\to \infty }\nu _n(F_n)<\infty $
. For a point
$\mu (X)=\lim _{n\to \infty }\nu _n(F_n)<\infty $
. For a point ![]() , we let
, we let
whenever this limit exists. (The quotient space
![]() $G/\Gamma $
is endowed with the discrete topology.) It follows from the Borel–Cantelli lemma that if
$G/\Gamma $
is endowed with the discrete topology.) It follows from the Borel–Cantelli lemma that if
![]() $\mathcal T$
is compatible with
$\mathcal T$
is compatible with
![]() ${g\Gamma \in G/\Gamma }$
, then
${g\Gamma \in G/\Gamma }$
, then
![]() $\pi _{({\mathcal T},g\Gamma )}(x)$
is well defined for
$\pi _{({\mathcal T},g\Gamma )}(x)$
is well defined for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in X_0$
. It is straightforward to verify that for each
$x\in X_0$
. It is straightforward to verify that for each
![]() $h\in G$
,
$h\in G$
,
whenever
![]() $\pi _{({\mathcal T},g\Gamma )}( x)$
is well defined and
$\pi _{({\mathcal T},g\Gamma )}( x)$
is well defined and
![]() $ T_h x\in X_0$
. It follows that the mapping
$ T_h x\in X_0$
. It follows that the mapping
extends uniquely (mod 0) to a measurable G-equivariant mapping from
![]() $ X$
to
$ X$
to
![]() $G/\Gamma $
. We denote the extension by the same symbol
$G/\Gamma $
. We denote the extension by the same symbol
![]() $\pi _{(\mathcal T,g\Gamma )}$
. It is routine to verify that if
$\pi _{(\mathcal T,g\Gamma )}$
. It is routine to verify that if
![]() $x=( f_n, c_{n+1}, c_{n+2},\ldots )\in X_n$
for some
$x=( f_n, c_{n+1}, c_{n+2},\ldots )\in X_n$
for some
![]() $n\in \mathbb N$
, then
$n\in \mathbb N$
, then
Definition 3.2. We call
![]() $\pi _{({\mathcal T},g\Gamma )}$
the
$\pi _{({\mathcal T},g\Gamma )}$
the
![]() $({\mathcal T},g\Gamma )$
-factor mapping for T.
$({\mathcal T},g\Gamma )$
-factor mapping for T.
We need some notation. Given
![]() $1<n<m$
, we denote the subset
$1<n<m$
, we denote the subset ![]() of G by
of G by
![]() $C_{n,m}$
. Let
$C_{n,m}$
. Let
![]() $\kappa _{n,m}$
stand for the probability measure
$\kappa _{n,m}$
stand for the probability measure ![]() . It is supported on
. It is supported on ![]() . We now state the main result of the section.
. We now state the main result of the section.
Theorem 3.3. The following are equivalent.
-
(i) There is a measurable factor map
 $\tau : X\to G/\Gamma $
, that is, for each
$\tau : X\to G/\Gamma $
, that is, for each
 $g\in G$
,
$g\in G$
,  $$ \begin{align*} \tau(T_gx)=g\tau(x)\quad\text{at}\ \mu-\text{a.e.}\ x\in X. \end{align*} $$
$$ \begin{align*} \tau(T_gx)=g\tau(x)\quad\text{at}\ \mu-\text{a.e.}\ x\in X. \end{align*} $$
-
(ii) There exists a sequence
 $(g_n)_{n>0}$
of elements of G such that
$(g_n)_{n>0}$
of elements of G such that  $$ \begin{align*} \lim\limits_{N\to\infty}\sup\limits_{m> n\geq N}\kappa_{n+1,m} (\{c\in C_{n+1,m} \mid c\notin g_n^{-1}\Gamma g_m\}) = 0. \end{align*} $$
$$ \begin{align*} \lim\limits_{N\to\infty}\sup\limits_{m> n\geq N}\kappa_{n+1,m} (\{c\in C_{n+1,m} \mid c\notin g_n^{-1}\Gamma g_m\}) = 0. \end{align*} $$
-
(iii) There exist a coset
 $g_0\Gamma \in G/\Gamma $
and a
$g_0\Gamma \in G/\Gamma $
and a
 $g_0\Gamma $
-compatible telescoping of
$g_0\Gamma $
-compatible telescoping of
 $\mathcal T$
.
$\mathcal T$
.
It follows that T has no factors isomorphic to
![]() $G/\Gamma $
if and only if there is no telescoping of
$G/\Gamma $
if and only if there is no telescoping of
![]() $\mathcal T$
compatible with
$\mathcal T$
compatible with
![]() $g\Gamma g^{-1}$
for any
$g\Gamma g^{-1}$
for any
![]() $g\in G$
.
$g\in G$
.
Proof. (i)
![]() $\Longrightarrow $
(ii) Let
$\Longrightarrow $
(ii) Let
![]() $Y_j := \tau ^{-1}(j)$
for each
$Y_j := \tau ^{-1}(j)$
for each
![]() $j\in G/\Gamma $
. Then,
$j\in G/\Gamma $
. Then,
![]() $X=\bigsqcup _{j\in G/\Gamma }Y_j$
. Consider n large so that
$X=\bigsqcup _{j\in G/\Gamma }Y_j$
. Consider n large so that
![]() $\mu (Y_j\cap X_n)>0$
for each
$\mu (Y_j\cap X_n)>0$
for each
![]() $j\in G/\Gamma $
. Let
$j\in G/\Gamma $
. Let
![]() $g,h\in F_n$
. Since
$g,h\in F_n$
. Since
![]() $\tau $
is G-equivariant, it follows that
$\tau $
is G-equivariant, it follows that
![]() $T_{hg^{-1}} Y_j = Y_{hg^{-1}j}$
and hence,
$T_{hg^{-1}} Y_j = Y_{hg^{-1}j}$
and hence,
For each
![]() $j\in G/\Gamma $
and
$j\in G/\Gamma $
and
![]() $g \in F_n$
, let
$g \in F_n$
, let
Then, the set
![]() $\{d_{n, g}(j)\mid j\in G/\Gamma \}\subset (0,1)$
does not depend on
$\{d_{n, g}(j)\mid j\in G/\Gamma \}\subset (0,1)$
does not depend on
![]() $g\in F_n$
. Indeed, for each
$g\in F_n$
. Indeed, for each
![]() $h\in F_n$
, the Radon–Nikodym derivative of the transformation
$h\in F_n$
, the Radon–Nikodym derivative of the transformation
![]() $T_{gh^{-1}}$
is constant on
$T_{gh^{-1}}$
is constant on
![]() $[h]_n$
and we deduce from equation (3.2) that
$[h]_n$
and we deduce from equation (3.2) that
 $$ \begin{align} d_{n,h}(j) := \frac{\mu([h]_n\cap Y_j)}{\mu([h]_n)} = \frac{\mu([g]_n\cap Y_{gh^{-1}j})}{\mu([g]_n)}=d_{n,g}(gh^{-1}j). \end{align} $$
$$ \begin{align} d_{n,h}(j) := \frac{\mu([h]_n\cap Y_j)}{\mu([h]_n)} = \frac{\mu([g]_n\cap Y_{gh^{-1}j})}{\mu([g]_n)}=d_{n,g}(gh^{-1}j). \end{align} $$
Hence,
![]() $ \{d_{n, h}(j): j\in G/\Gamma \} = \{d_{n, g}(j): j\in G/\Gamma \}. $
Let
$ \{d_{n, h}(j): j\in G/\Gamma \} = \{d_{n, g}(j): j\in G/\Gamma \}. $
Let
We claim that
![]() $\delta _m \to 1$
as
$\delta _m \to 1$
as
![]() $m\to \infty $
. Indeed, for
$m\to \infty $
. Indeed, for
![]() $m\ge n$
, let
$m\ge n$
, let
![]() ${\mathcal P}_m$
denote the finite
${\mathcal P}_m$
denote the finite
![]() $\sigma $
-algebra generated by the m-cylinders (which are compact and open subsets of X) that are contained in
$\sigma $
-algebra generated by the m-cylinders (which are compact and open subsets of X) that are contained in
![]() $X_n$
. Then,
$X_n$
. Then, ![]() and
and
![]() $\bigvee _{m>n}{\mathcal P}_m$
is the entire Borel
$\bigvee _{m>n}{\mathcal P}_m$
is the entire Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $X_n$
. Hence, for each
$X_n$
. Hence, for each
![]() $j\in G/\Gamma $
, there is
$j\in G/\Gamma $
, there is
![]() $g_m\in F_m$
such that
$g_m\in F_m$
such that
This implies that
![]() $\delta _m \to 1$
as
$\delta _m \to 1$
as
![]() $m\to \infty $
, as claimed. In what follows, we consider n large so that
$m\to \infty $
, as claimed. In what follows, we consider n large so that
![]() $\delta _n> 0.9$
. Then for each
$\delta _n> 0.9$
. Then for each
![]() $g\in F_n$
, there is a unique
$g\in F_n$
, there is a unique
![]() $\Gamma $
-coset
$\Gamma $
-coset
![]() $j_n(g)\in G/\Gamma $
such that
$j_n(g)\in G/\Gamma $
such that
![]() $\delta _n=d_{n,g}(j_n(g))$
. It is convenient to consider
$\delta _n=d_{n,g}(j_n(g))$
. It is convenient to consider
![]() $G/\Gamma $
as a set of colours. Then,
$G/\Gamma $
as a set of colours. Then,
![]() $j_n(g)$
is the dominating colour on
$j_n(g)$
is the dominating colour on
![]() $[g]_n$
. It follows from equation (3.3) that
$[g]_n$
. It follows from equation (3.3) that
![]() $j_n(g)=gh^{-1} j_n(h)$
for all
$j_n(g)=gh^{-1} j_n(h)$
for all
![]() $g,h\in F_n$
. Choose
$g,h\in F_n$
. Choose
![]() $g_n\in F_n$
such that
$g_n\in F_n$
such that
![]() $j_n(g_n) = \Gamma $
. Then,
$j_n(g_n) = \Gamma $
. Then,
![]() $j_n(g)= gg_n^{-1} \Gamma $
for each
$j_n(g)= gg_n^{-1} \Gamma $
for each
![]() $g\in F_n$
. Given
$g\in F_n$
. Given
![]() $\epsilon < \tfrac {1}{2}$
, there is
$\epsilon < \tfrac {1}{2}$
, there is
![]() $N> 0$
such that
$N> 0$
such that
![]() $\delta _n> 1-\epsilon ^2$
for all
$\delta _n> 1-\epsilon ^2$
for all
![]() $n> N$
. Hence, for all
$n> N$
. Hence, for all
![]() $m> n > N$
,
$m> n > N$
,
We recall that
![]() $[1_G]_n=\bigsqcup _{c\in C_{n+1,m}}[c]_m$
. Let
$[1_G]_n=\bigsqcup _{c\in C_{n+1,m}}[c]_m$
. Let
It follows from equation (3.4) that
 $$ \begin{align*} \begin{aligned} (1-\epsilon^2)\mu([1_G]_n)&<\sum_{c\in D}\mu([c]_m)+(1-\epsilon)\sum_{c\in C_{n+1,m}\setminus D}\mu([c]_m)\\ &=\sum_{c\in D}\mu([c]_m)+(1-\epsilon)\bigg(\mu([1_G]_n)-\sum_{c\in D}\mu([c]_m)\bigg). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (1-\epsilon^2)\mu([1_G]_n)&<\sum_{c\in D}\mu([c]_m)+(1-\epsilon)\sum_{c\in C_{n+1,m}\setminus D}\mu([c]_m)\\ &=\sum_{c\in D}\mu([c]_m)+(1-\epsilon)\bigg(\mu([1_G]_n)-\sum_{c\in D}\mu([c]_m)\bigg). \end{aligned} \end{align*} $$
This yields that
![]() $\sum _{c\in D}\mu ([c]_m)>(1-\epsilon )\mu ([1_G]_n)$
or, equivalently,
$\sum _{c\in D}\mu ([c]_m)>(1-\epsilon )\mu ([1_G]_n)$
or, equivalently,
By the definition of D, an element
![]() $c\in C_{n+1,m}$
belongs to D if and only if
$c\in C_{n+1,m}$
belongs to D if and only if
![]() $j_n(1_G)$
is the dominating colour on
$j_n(1_G)$
is the dominating colour on
![]() $[c]_m$
, that is,
$[c]_m$
, that is,
![]() $j_m(c)=j_n(1_G)$
. Therefore,
$j_m(c)=j_n(1_G)$
. Therefore,
![]() $cg_m^{-1}\Gamma =g_n^{-1}\Gamma $
, that is,
$cg_m^{-1}\Gamma =g_n^{-1}\Gamma $
, that is,
![]() $c\in g_n^{-1}\Gamma g_m$
. Hence, equation (3.5) yields that
$c\in g_n^{-1}\Gamma g_m$
. Hence, equation (3.5) yields that
and property (ii) follows.
(ii)
![]() $\Longrightarrow $
(iii) As
$\Longrightarrow $
(iii) As
![]() $\Gamma $
is cofinite and property (ii) holds, there exist an increasing sequence
$\Gamma $
is cofinite and property (ii) holds, there exist an increasing sequence ![]() of positive integers and an element
of positive integers and an element
![]() $g_0\in G$
such that
$g_0\in G$
such that
![]() $g_n^{-1}\in g_0\Gamma $
and
$g_n^{-1}\in g_0\Gamma $
and
for each
![]() $n\in \mathbb N$
. Let
$n\in \mathbb N$
. Let
![]() $\boldsymbol q:=(q_n)_{n=0}^\infty $
. Then
$\boldsymbol q:=(q_n)_{n=0}^\infty $
. Then
![]() $g_0\Gamma $
is compatible with the
$g_0\Gamma $
is compatible with the
![]() $\boldsymbol q$
-telescoping of
$\boldsymbol q$
-telescoping of
![]() $\mathcal T$
. This implies property (iii).
$\mathcal T$
. This implies property (iii).
(iii)
![]() $\Longrightarrow $
(i) Denote by
$\Longrightarrow $
(i) Denote by
![]() $\widetilde {\mathcal T}$
the
$\widetilde {\mathcal T}$
the
![]() $\boldsymbol q$
-telescoping of
$\boldsymbol q$
-telescoping of
![]() $\mathcal T$
. Then
$\mathcal T$
. Then
![]() $\pi _{(\widetilde {\mathcal T},g_0\Gamma )}\circ \iota _{\boldsymbol q}$
is a factor mapping of T onto
$\pi _{(\widetilde {\mathcal T},g_0\Gamma )}\circ \iota _{\boldsymbol q}$
is a factor mapping of T onto
![]() $G/\Gamma $
.
$G/\Gamma $
.
Thus, the first statement of the theorem is proved completely. The second statement follows from the first one and a simple observation that given two subgroups
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
of G, the corresponding G-actions by left translations on
$\Gamma '$
of G, the corresponding G-actions by left translations on
![]() $G/\Gamma $
and
$G/\Gamma $
and
![]() $G/\Gamma '$
are isomorphic if and only if
$G/\Gamma '$
are isomorphic if and only if
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
are conjugate.
$\Gamma '$
are conjugate.
The following important remark will be used essentially in the proof of the main result of §4.
Remark 3.4. In fact, we obtained more than what is stated in Theorem 3.3. We proved indeed that given a factor mapping
![]() $\tau :X\to G/\Gamma $
, there exist a coset
$\tau :X\to G/\Gamma $
, there exist a coset
![]() $g_0\Gamma $
and a
$g_0\Gamma $
and a
![]() $g_0\Gamma $
-compatible
$g_0\Gamma $
-compatible
![]() $\boldsymbol q$
-telescoping
$\boldsymbol q$
-telescoping
![]() $\widetilde {\mathcal T}$
of
$\widetilde {\mathcal T}$
of
![]() $\mathcal T$
such that
$\mathcal T$
such that
![]() $\tau =\pi _{(\widetilde {\mathcal T},g_0\Gamma )}\circ \iota _{\boldsymbol q}$
. To explain this fact, we use below the notation from the proof of Theorem 3.3. For
$\tau =\pi _{(\widetilde {\mathcal T},g_0\Gamma )}\circ \iota _{\boldsymbol q}$
. To explain this fact, we use below the notation from the proof of Theorem 3.3. For
![]() $n\in \mathbb N$
, let
$n\in \mathbb N$
, let
 $$ \begin{align*} X_n':=\bigsqcup_{f_n\in F_n} ([f_n]_n\cap Y_{j_n(f_n)})\subset X_n. \end{align*} $$
$$ \begin{align*} X_n':=\bigsqcup_{f_n\in F_n} ([f_n]_n\cap Y_{j_n(f_n)})\subset X_n. \end{align*} $$
We remind that
![]() $\mu (X)<\infty $
. Since
$\mu (X)<\infty $
. Since
![]() $\delta _n\to 1$
and
$\delta _n\to 1$
and
![]() $\mu (X_n)\to \mu (X)$
as
$\mu (X_n)\to \mu (X)$
as
![]() $n\to \infty $
, it follows that
$n\to \infty $
, it follows that
![]() $\mu (X_{q_n}') \to \mu (X)$
as
$\mu (X_{q_n}') \to \mu (X)$
as
![]() $n\to \infty $
. We can assume (passing to a subsequence of
$n\to \infty $
. We can assume (passing to a subsequence of
![]() $(q_n)_{n=1}^\infty $
if needed) that
$(q_n)_{n=1}^\infty $
if needed) that
![]() $\sum \limits _{n=1}^{\infty } \mu (X\setminus X_{q_n}') < \infty $
. Then, the Borel–Cantelli lemma yields that for a.e.
$\sum \limits _{n=1}^{\infty } \mu (X\setminus X_{q_n}') < \infty $
. Then, the Borel–Cantelli lemma yields that for a.e.
![]() $x\in X$
, we have that
$x\in X$
, we have that
![]() $x\in X_{q_n}'$
eventually in n. Hence, for a.e.
$x\in X_{q_n}'$
eventually in n. Hence, for a.e.
![]() $x\in X$
,
$x\in X$
,
where
![]() $f_{q_m}$
is the first coordinate of x in
$f_{q_m}$
is the first coordinate of x in
![]() $X_{q_m}$
, that is,
$X_{q_m}$
, that is,
![]() $x=(f_{q_m}, c_{q_m+1},\ldots )\in X_{q_m}$
. Howerver, it follows from equations (3.1) and (3.2) that
$x=(f_{q_m}, c_{q_m+1},\ldots )\in X_{q_m}$
. Howerver, it follows from equations (3.1) and (3.2) that
at a.e.
![]() $x\in X$
. Therefore, equations (3.6) and (3.7) yield that
$x\in X$
. Therefore, equations (3.6) and (3.7) yield that
![]() $ \tau = \pi _{(\widetilde{\mathcal T}, g_0\Gamma )}\circ \iota _{\boldsymbol q}$
almost everywhere, as desired.
$ \tau = \pi _{(\widetilde{\mathcal T}, g_0\Gamma )}\circ \iota _{\boldsymbol q}$
almost everywhere, as desired.
We note in this connection that if:
-
• G is Abelian or G is arbitrary but
 $\Gamma $
is normal in G; and
$\Gamma $
is normal in G; and -
• the homogeneous space
 $G/\Gamma $
is a factor of an ergodic non-singular free action of G on a standard measure space
$G/\Gamma $
is a factor of an ergodic non-singular free action of G on a standard measure space  ,
,
then this factor (considered as an invariant sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of ![]() ) is defined uniquely by
) is defined uniquely by
![]() $\Gamma $
. Indeed, if
$\Gamma $
. Indeed, if
![]() $\pi _1,\pi _2:Y\to G/\Gamma $
are two G-equivariant measurable maps, then the mapping
$\pi _1,\pi _2:Y\to G/\Gamma $
are two G-equivariant measurable maps, then the mapping
![]() $Y\ni y\mapsto \pi _1(y)\pi _2(y)^{-1}\in G/\Gamma $
is invariant under G. Hence, it is constant. Therefore, there is
$Y\ni y\mapsto \pi _1(y)\pi _2(y)^{-1}\in G/\Gamma $
is invariant under G. Hence, it is constant. Therefore, there is
![]() $a\in G/\Gamma $
such that
$a\in G/\Gamma $
such that
![]() $\pi _1(y)=a\pi _2(y)$
for a.e.
$\pi _1(y)=a\pi _2(y)$
for a.e.
![]() $y\in Y$
. It follows that
$y\in Y$
. It follows that
Therefore, the equality
![]() $ \tau = \pi _{(\widetilde {\mathcal T}, g_0\Gamma )}\circ \iota _{\boldsymbol q}$
(at least, up to a rotation of
$ \tau = \pi _{(\widetilde {\mathcal T}, g_0\Gamma )}\circ \iota _{\boldsymbol q}$
(at least, up to a rotation of
![]() $G/\Gamma $
) stated in Remark 3.4 is a trivial fact. However, it is no longer true if
$G/\Gamma $
) stated in Remark 3.4 is a trivial fact. However, it is no longer true if
![]() $\Gamma $
is not normal.
$\Gamma $
is not normal.
Example 3.5. Let
![]() ${\mathbb Z}_3:={\mathbb Z}/3{\mathbb Z}$
,
${\mathbb Z}_3:={\mathbb Z}/3{\mathbb Z}$
,
![]() ${\mathbb Z}_2:={\mathbb Z}/2{\mathbb Z}$
,
${\mathbb Z}_2:={\mathbb Z}/2{\mathbb Z}$
,
![]() $G={\mathbb Z}_3\rtimes {\mathbb Z}_2$
and
$G={\mathbb Z}_3\rtimes {\mathbb Z}_2$
and
![]() $\Gamma = \{0\}\times {\mathbb Z}_2$
. Then
$\Gamma = \{0\}\times {\mathbb Z}_2$
. Then
![]() $\Gamma $
is a non-normal cofinite subgroup of G of index
$\Gamma $
is a non-normal cofinite subgroup of G of index
![]() $3$
. We consider
$3$
. We consider
![]() ${\mathbb Z}_3$
as a quotient
${\mathbb Z}_3$
as a quotient
![]() $G/\Gamma $
. Then
$G/\Gamma $
. Then
![]() ${\mathbb Z}_3$
is a G-space. Hence, the product space
${\mathbb Z}_3$
is a G-space. Hence, the product space
![]() ${\mathbb Z}_3\times {\mathbb Z}_3$
is also a G-space (we consider the diagonal G-action). Since the diagonal
${\mathbb Z}_3\times {\mathbb Z}_3$
is also a G-space (we consider the diagonal G-action). Since the diagonal
![]() $D=\{(j,j)\mid j\in G/\Gamma \}$
is an invariant subspace of
$D=\{(j,j)\mid j\in G/\Gamma \}$
is an invariant subspace of
![]() ${\mathbb Z}_3\times {\mathbb Z}_3$
, the complement
${\mathbb Z}_3\times {\mathbb Z}_3$
, the complement
![]() $Y:=({\mathbb Z}_3\times {\mathbb Z}_3)\setminus D$
of D in
$Y:=({\mathbb Z}_3\times {\mathbb Z}_3)\setminus D$
of D in
![]() ${\mathbb Z}_3\times {\mathbb Z}_3$
is also G-invariant. It is easy to verify that the G-action on Y is transitive and free. Endow Y with the (unique) G-invariant probability measure
${\mathbb Z}_3\times {\mathbb Z}_3$
is also G-invariant. It is easy to verify that the G-action on Y is transitive and free. Endow Y with the (unique) G-invariant probability measure
![]() $\nu $
. Of course, the coordinate projections
$\nu $
. Of course, the coordinate projections
![]() ${\pi _1,\pi _2:Y\to {\mathbb Z}_3}$
are two-to-one G-equivariant maps. However, the corresponding
${\pi _1,\pi _2:Y\to {\mathbb Z}_3}$
are two-to-one G-equivariant maps. However, the corresponding
![]() $\sigma $
-algebras of
$\sigma $
-algebras of
![]() $\pi _1$
-measurable and
$\pi _1$
-measurable and
![]() $\pi _2$
-measurable subsets in Y are different. Consider a rank-one
$\pi _2$
-measurable subsets in Y are different. Consider a rank-one
![]() ${\mathbb Z}$
-action on a standard probability space
${\mathbb Z}$
-action on a standard probability space ![]() . Then the product
. Then the product
![]() $({\mathbb Z}\times G)$
-action on
$({\mathbb Z}\times G)$
-action on
![]() $(Z\times Y,\kappa \otimes \nu )$
is of rank one. Denote it by R. The subgroup
$(Z\times Y,\kappa \otimes \nu )$
is of rank one. Denote it by R. The subgroup
![]() ${\mathbb Z}\times \Gamma $
of
${\mathbb Z}\times \Gamma $
of
![]() ${\mathbb Z}\times G$
is non-normal. It is of index 3. Hence, we can consider the corresponding finite quotient space
${\mathbb Z}\times G$
is non-normal. It is of index 3. Hence, we can consider the corresponding finite quotient space
![]() ${\mathbb Z}_3$
as a
${\mathbb Z}_3$
as a
![]() $({\mathbb Z}\times G)$
-space. The mappings
$({\mathbb Z}\times G)$
-space. The mappings
![]() $1\otimes \pi _1$
and
$1\otimes \pi _1$
and
![]() $1\otimes \pi _2$
from
$1\otimes \pi _2$
from
![]() $Z\times Y$
onto
$Z\times Y$
onto
![]() ${\mathbb Z}_3$
are
${\mathbb Z}_3$
are
![]() $({\mathbb Z}\times G)$
-equivariant. However, the corresponding factors of R, that is, the invariant sub-
$({\mathbb Z}\times G)$
-equivariant. However, the corresponding factors of R, that is, the invariant sub-
![]() $\sigma $
-algebras, are different.
$\sigma $
-algebras, are different.
A non-singular G-action is totally ergodic if and only if it has no non-trivial finite factors or, equivalently, each cofinite subgroup of G acts ergodically. We thus deduce from Theorem 3.3 the following criterion of total ergodicity for the rank-one non-singular actions.
Corollary 3.6. Let T be a
![]() $(C,F)$
-action of G associated with a sequence
$(C,F)$
-action of G associated with a sequence
![]() $\mathcal T$
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then, T is totally ergodic if no telescoping of
$\mathcal T$
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then, T is totally ergodic if no telescoping of
![]() $\mathcal T$
is compatible with any proper cofinite subgroup of
$\mathcal T$
is compatible with any proper cofinite subgroup of
![]() $ G$
, that is, for each increasing sequence
$ G$
, that is, for each increasing sequence ![]() of integers and each proper cofinite subgroup
of integers and each proper cofinite subgroup
![]() $\Gamma $
in G,
$\Gamma $
in G,

4. Non-singular odometer actions of residually finite groups
4.1. Non-singular odometers
From now on, G is residually finite. If
![]() $\Gamma $
is a cofinite subgroup in G, then the largest subgroup
$\Gamma $
is a cofinite subgroup in G, then the largest subgroup
![]() $\widetilde \Gamma $
of
$\widetilde \Gamma $
of
![]() $\Gamma $
which is normal in G is also cofinite in G. Of course,
$\Gamma $
which is normal in G is also cofinite in G. Of course,
![]() $\widetilde \Gamma =\bigcap _{g\in G}g\Gamma g^{-1}$
. If
$\widetilde \Gamma =\bigcap _{g\in G}g\Gamma g^{-1}$
. If
![]() $\Xi $
is cofinite subgroup in
$\Xi $
is cofinite subgroup in
![]() $\Gamma $
, then
$\Gamma $
, then
![]() $\widetilde \Xi \subset \widetilde \Gamma $
. We now fix a decreasing sequence
$\widetilde \Xi \subset \widetilde \Gamma $
. We now fix a decreasing sequence ![]() of cofinite subgroups
of cofinite subgroups
![]() $\Gamma _n$
in G such that
$\Gamma _n$
in G such that
 $$ \begin{align} \bigcap_{n=1}^\infty\bigcap_{g\in G}g\Gamma_ng^{-1}=\{1_G\}. \end{align} $$
$$ \begin{align} \bigcap_{n=1}^\infty\bigcap_{g\in G}g\Gamma_ng^{-1}=\{1_G\}. \end{align} $$
It exists because G is residually finite. We note that equation (4.1) means that the intersection of the maximal normal (in G) subgroups of
![]() $\Gamma _n$
,
$\Gamma _n$
,
![]() $n\in \mathbb N$
, is trivial. At the same time, the intersection of all
$n\in \mathbb N$
, is trivial. At the same time, the intersection of all
![]() $\Gamma _n$
can be non-trivial. Consider the natural inverse sequence of homogeneous G-spaces and G-equivariant mappings intertwining them:
$\Gamma _n$
can be non-trivial. Consider the natural inverse sequence of homogeneous G-spaces and G-equivariant mappings intertwining them:
Denote by Y the projective limit of this sequence. A point of Y is a sequence
![]() $(g_n\Gamma _n)_{n=1}^\infty $
such that
$(g_n\Gamma _n)_{n=1}^\infty $
such that
![]() $g_n\Gamma _n=g_{n+1}\Gamma _n$
, that is,
$g_n\Gamma _n=g_{n+1}\Gamma _n$
, that is,
![]() $g_n^{-1}g_{n+1}\in \Gamma _n$
for each
$g_n^{-1}g_{n+1}\in \Gamma _n$
for each
![]() $n>0$
. Endow Y with the topology of projective limit. Then Y is a compact Cantor G-space. Of course, the G-action on Y is minimal and uniquely ergodic. Denote this action by
$n>0$
. Endow Y with the topology of projective limit. Then Y is a compact Cantor G-space. Of course, the G-action on Y is minimal and uniquely ergodic. Denote this action by
![]() $O=(O_g)_{g\in G}$
. It follows from equation (4.1) that O is faithful, that is,
$O=(O_g)_{g\in G}$
. It follows from equation (4.1) that O is faithful, that is,
![]() $O_g\ne I$
if
$O_g\ne I$
if
![]() $g\ne 1_G$
. We note that a faithful action is not necessarily free.
$g\ne 1_G$
. We note that a faithful action is not necessarily free.
Definition 4.1. The dynamical system
![]() $(Y,O)$
is called the topological G-odometer associated with
$(Y,O)$
is called the topological G-odometer associated with
![]() $(\Gamma _n)_{n=1}^\infty $
. If
$(\Gamma _n)_{n=1}^\infty $
. If
![]() $\nu $
is a non-atomic Borel measure on Y which is quasi-invariant and ergodic under O, then we call the dynamical system
$\nu $
is a non-atomic Borel measure on Y which is quasi-invariant and ergodic under O, then we call the dynamical system
![]() $(Y,\nu ,O)$
a non-singular G-odometer. By the Haar measure for
$(Y,\nu ,O)$
a non-singular G-odometer. By the Haar measure for
![]() $(Y,O)$
, we mean the unique G-invariant probability on Y.
$(Y,O)$
, we mean the unique G-invariant probability on Y.
In the finite measure preserving case, one can find the above definition in [Reference Danilenko and LemańczykDaLe] (see also [Reference Lightwood, Şahin and UgarcoviciLiSaUg], where odometers are called ‘subodometers’.)
We note that equation (4.1) is in no way restrictive. Indeed, let
![]() $\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=N\ne \{1_G\}$
. Define
$\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Gamma _ng^{-1}=N\ne \{1_G\}$
. Define
![]() $(Y,O)$
as above. Then, N is a proper normal subgroup of G and
$(Y,O)$
as above. Then, N is a proper normal subgroup of G and
![]() $N=\{g\in G\mid O_g=I\}$
. We now let
$N=\{g\in G\mid O_g=I\}$
. We now let
![]() $\widetilde G:=G/N$
and
$\widetilde G:=G/N$
and
![]() $\widetilde \Gamma _n:=\Gamma _n/N$
. Then,
$\widetilde \Gamma _n:=\Gamma _n/N$
. Then,
![]() $\widetilde \Gamma _n$
is a cofinite subgroup in
$\widetilde \Gamma _n$
is a cofinite subgroup in
![]() $\widetilde G$
for each
$\widetilde G$
for each
![]() $n\in \mathbb N$
,
$n\in \mathbb N$
, ![]() and
and
![]() $\bigcap _{n=1}^\infty \bigcap _{g\in \widetilde G}g\widetilde \Gamma _ng^{-1}=\{1_{\widetilde G}\}$
. Let
$\bigcap _{n=1}^\infty \bigcap _{g\in \widetilde G}g\widetilde \Gamma _ng^{-1}=\{1_{\widetilde G}\}$
. Let
![]() $(\widetilde Y,\widetilde O)$
denote the topological
$(\widetilde Y,\widetilde O)$
denote the topological
![]() $\widetilde G$
-odometer associated with the sequence
$\widetilde G$
-odometer associated with the sequence
![]() $(\widetilde \Gamma _n)_{n=1}^\infty $
. Then, of course,
$(\widetilde \Gamma _n)_{n=1}^\infty $
. Then, of course,
![]() $Y=\widetilde Y$
and
$Y=\widetilde Y$
and
![]() $O_g=\widetilde O_{gN}$
for each
$O_g=\widetilde O_{gN}$
for each
![]() $g\in G$
.
$g\in G$
.
We now isolate a class of non-singular odometers of rank one. For each
![]() $n>0$
, we choose a finite subset
$n>0$
, we choose a finite subset
![]() $D_n\subset \Gamma _{n-1}$
such that
$D_n\subset \Gamma _{n-1}$
such that
![]() $1_G\in D_n$
and each
$1_G\in D_n$
and each
![]() $\Gamma _{n}$
-coset in
$\Gamma _{n}$
-coset in
![]() $\Gamma _{n-1}$
intersects
$\Gamma _{n-1}$
intersects
![]() $D_n$
exactly once. (For consistency of the notation, we let
$D_n$
exactly once. (For consistency of the notation, we let
![]() $\Gamma _0:=G$
.) We then call
$\Gamma _0:=G$
.) We then call
![]() $D_n$
a
$D_n$
a
![]() $\Gamma _n$
-cross-section in
$\Gamma _n$
-cross-section in
![]() $\Gamma _{n-1}$
. Then, the product
$\Gamma _{n-1}$
. Then, the product ![]() is a
is a
![]() $\Gamma _n$
-cross-section in G. Hence, there is a unique bijection
$\Gamma _n$
-cross-section in G. Hence, there is a unique bijection
such that
![]() $\omega _n(g\Gamma _n)\Gamma _n=g\Gamma _n$
for each
$\omega _n(g\Gamma _n)\Gamma _n=g\Gamma _n$
for each
![]() $g\in G$
and
$g\in G$
and
![]() $\omega _n(\Gamma _n)=1_G$
. It follows, in particular, that
$\omega _n(\Gamma _n)=1_G$
. It follows, in particular, that
It is straightforward to verify that the diagram

commutes. The horizontal arrows in the upper line denote the natural projections. The other mappings in the diagram are defined as follows:

for each ![]() and
and
![]() $n\ge 0$
. It follows from equation (4.3) that there exists a natural homeomorphism of Y onto the infinite product space
$n\ge 0$
. It follows from equation (4.3) that there exists a natural homeomorphism of Y onto the infinite product space ![]() . (The homeomorphism pushes down to a bijection between
. (The homeomorphism pushes down to a bijection between
![]() $G/\Gamma _n$
and
$G/\Gamma _n$
and ![]() for each n.)
for each n.)
Proposition 4.2. If, for each
![]() $n\in \mathbb N$
, there is a
$n\in \mathbb N$
, there is a
![]() $\Gamma _n$
-cross-section
$\Gamma _n$
-cross-section
![]() $D_n$
in
$D_n$
in
![]() $\Gamma _{n-1}$
and a probability
$\Gamma _{n-1}$
and a probability
![]() $\kappa _n$
on G such that:
$\kappa _n$
on G such that:
-
(i)
 $\mathrm {supp}\, \kappa _n=D_n$
for each n;
$\mathrm {supp}\, \kappa _n=D_n$
for each n; -
(ii)
 $\prod _{n=1}^\infty \max _{d\in D_n}\kappa _n(d)=0$
; and
$\prod _{n=1}^\infty \max _{d\in D_n}\kappa _n(d)=0$
; and -
(iii)
 for each
for each
 $g\in G$
,
$g\in G$
,
then there is a non-atomic probability Borel measure
![]() $\mu $
on Y which is quasi-invariant under O and such that the non-singular odometer
$\mu $
on Y which is quasi-invariant under O and such that the non-singular odometer
![]() $(Y,\mu ,O)$
is of rank one along the sequence
$(Y,\mu ,O)$
is of rank one along the sequence ![]() .
.
Proof. We set
![]() $F_0:=\{1_G\}$
,
$F_0:=\{1_G\}$
, ![]() ,
,
![]() $C_n:=D_n$
and
$C_n:=D_n$
and ![]() for each
for each
![]() $n\in \mathbb N$
. Then equations (2.1)–(2.3) hold for the sequence
$n\in \mathbb N$
. Then equations (2.1)–(2.3) hold for the sequence
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Moreover, Proposition 2.10(iii) is exactly property (iii) in the case under consideration. Hence, the
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Moreover, Proposition 2.10(iii) is exactly property (iii) in the case under consideration. Hence, the
![]() $(C,F)$
-action T of G associated with
$(C,F)$
-action T of G associated with
![]() $(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
is well defined. Let
$(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
is well defined. Let
![]() $(X,\mu )$
stand for the space of this action. It follows from the
$(X,\mu )$
stand for the space of this action. It follows from the
![]() $(C,F)$
-construction that
$(C,F)$
-construction that
![]() $\mu $
is non-atomic and T is free (mod
$\mu $
is non-atomic and T is free (mod
![]() $\mu $
). In view of equation (4.3), we can identify X with Y. Hence, we consider
$\mu $
). In view of equation (4.3), we can identify X with Y. Hence, we consider
![]() $\mu $
as a probability on Y. Moreover, equation (4.2) yields that T is conjugate to O. Thus,
$\mu $
as a probability on Y. Moreover, equation (4.2) yields that T is conjugate to O. Thus,
![]() $(Y,\mu ,O)$
is a non-singular odometer. It remains to apply Theorem 2.13.
$(Y,\mu ,O)$
is a non-singular odometer. It remains to apply Theorem 2.13.
We now show that the classical non-singular
![]() ${\mathbb Z}$
-odometers of product type are covered by Definition 4.1.
${\mathbb Z}$
-odometers of product type are covered by Definition 4.1.
Example 4.3. Let
![]() $G={\mathbb Z}$
and let
$G={\mathbb Z}$
and let
![]() $(a_n)_{n=1}^\infty $
be a sequence of integers such that
$(a_n)_{n=1}^\infty $
be a sequence of integers such that
![]() $a_n>1$
for each
$a_n>1$
for each
![]() $n\in \mathbb N$
. We set
$n\in \mathbb N$
. We set ![]() . Then,
. Then, ![]() and
and
![]() $\bigcap _{n=1}^\infty \Gamma _n=\{0\}$
. The set
$\bigcap _{n=1}^\infty \Gamma _n=\{0\}$
. The set ![]() is a
is a
![]() $\Gamma _n$
-cross-section in
$\Gamma _n$
-cross-section in
![]() $\Gamma _{n-1}$
. Hence, in view of equation (4.4), the space Y of the
$\Gamma _{n-1}$
. Hence, in view of equation (4.4), the space Y of the
![]() ${\mathbb Z}$
-odometer
${\mathbb Z}$
-odometer
![]() $O=(O_n)_{n\in {\mathbb Z}}$
associated with
$O=(O_n)_{n\in {\mathbb Z}}$
associated with
![]() $(\Gamma _n)_{n=1}^\infty $
is homeomorphic to the infinite product
$(\Gamma _n)_{n=1}^\infty $
is homeomorphic to the infinite product ![]() . We identify
. We identify
![]() $D_n$
naturally with the set
$D_n$
naturally with the set
![]() $\{0,1,\ldots ,a_n-1\}$
. Then,
$\{0,1,\ldots ,a_n-1\}$
. Then,
To define O explicitly on this space, we take
![]() $y=(y_n)_{n=1}^\infty \in D$
. It is a routine to check that if there is
$y=(y_n)_{n=1}^\infty \in D$
. It is a routine to check that if there is
![]() $k> 0$
such that
$k> 0$
such that
![]() $y_j=a_{j}-1$
for each
$y_j=a_{j}-1$
for each
![]() $j<k$
and
$j<k$
and
![]() $y_k\ne a_k-1$
, then
$y_k\ne a_k-1$
, then
If such a k does not exist, that is,
![]() $y_j=a_j-1$
for each
$y_j=a_j-1$
for each
![]() $j>0$
, then
$j>0$
, then
![]() $O_1y=(0,0,\ldots )$
. Let
$O_1y=(0,0,\ldots )$
. Let
![]() $\kappa _n$
be a non-degenerated probability measure on
$\kappa _n$
be a non-degenerated probability measure on
![]() $\{0,1,\ldots ,a_n-1\}$
and let
$\{0,1,\ldots ,a_n-1\}$
and let
![]() $\prod _{n>0}\max _{0\le d<a_n}\kappa _n(d)=0$
. This means that properties (i) and (ii) of Proposition 4.2 hold. Of course, Proposition 4.2(iii) holds also. Hence, by Proposition 4.2, the non-singular odometer
$\prod _{n>0}\max _{0\le d<a_n}\kappa _n(d)=0$
. This means that properties (i) and (ii) of Proposition 4.2 hold. Of course, Proposition 4.2(iii) holds also. Hence, by Proposition 4.2, the non-singular odometer
 $$ \begin{align*} \bigg(\bigotimes_{n=1}^\infty \{0,\ldots,a_n-1\}, \bigotimes_{n=1}^\infty\kappa_n, O\bigg) \end{align*} $$
$$ \begin{align*} \bigg(\bigotimes_{n=1}^\infty \{0,\ldots,a_n-1\}, \bigotimes_{n=1}^\infty\kappa_n, O\bigg) \end{align*} $$
is of rank one. Thus, in this case, our definition of non-singular odometer coincides with the classical definition of non-singular
![]() ${\mathbb Z}$
-odometers of product type (see [Reference AaronsonAa, Reference Danilenko, Silva and MeyersDaSi]). Moreover, the
${\mathbb Z}$
-odometers of product type (see [Reference AaronsonAa, Reference Danilenko, Silva and MeyersDaSi]). Moreover, the
![]() ${\mathbb Z}$
-odometers of product type are of rank one.
${\mathbb Z}$
-odometers of product type are of rank one.
It is routine to verify that if
![]() $G={\mathbb Z}^d$
with
$G={\mathbb Z}^d$
with
![]() $d\in \mathbb N$
, then each probability preserving G-odometer is of rank one. This follows from Proposition 4.2 if one chooses the
$d\in \mathbb N$
, then each probability preserving G-odometer is of rank one. This follows from Proposition 4.2 if one chooses the
![]() $\Gamma _n$
-cross-sections
$\Gamma _n$
-cross-sections
![]() $D_n$
in
$D_n$
in
![]() $\Gamma _{n-1}$
in such a way that the sum
$\Gamma _{n-1}$
in such a way that the sum ![]() is a parallelepiped
is a parallelepiped ![]() for some
for some
![]() $a_{1,n},\ldots ,a_{d,n}\in \mathbb N$
with
$a_{1,n},\ldots ,a_{d,n}\in \mathbb N$
with
![]() $\lim _{n\to \infty }a_{j,n}=\infty $
for each j. We leave details to the reader (see also [Reference Johnson and McClendonJoMc, Theorem 2.11]).
$\lim _{n\to \infty }a_{j,n}=\infty $
for each j. We leave details to the reader (see also [Reference Johnson and McClendonJoMc, Theorem 2.11]).
Note, however, that there exist probability preserving free G-odometers which are not of rank one.
Example 4.4. The free group with two generators
![]() $\boldsymbol F_2$
is residually finite. Hence, there is a sequence
$\boldsymbol F_2$
is residually finite. Hence, there is a sequence ![]() of normal subgroups in
of normal subgroups in
![]() $\boldsymbol F_2$
such that
$\boldsymbol F_2$
such that
![]() $\bigcap _{n=1}^\infty N_n=\{1_{\boldsymbol F_2}\}$
. Then, the topological
$\bigcap _{n=1}^\infty N_n=\{1_{\boldsymbol F_2}\}$
. Then, the topological
![]() $\boldsymbol F_2$
-odometer associated with
$\boldsymbol F_2$
-odometer associated with
![]() $(N_n)_{n=1}^\infty $
is a free minimal
$(N_n)_{n=1}^\infty $
is a free minimal
![]() $\boldsymbol F_2$
-action by translation on a compact group Y. Let
$\boldsymbol F_2$
-action by translation on a compact group Y. Let
![]() $\chi $
denote the Haar measure on Y. Then,
$\chi $
denote the Haar measure on Y. Then,
![]() $(K,\chi , O)$
is an ergodic probability preserving
$(K,\chi , O)$
is an ergodic probability preserving
![]() $\boldsymbol F_2$
-odometer. If
$\boldsymbol F_2$
-odometer. If
![]() $(K,\chi , O)$
were of rank one, then
$(K,\chi , O)$
were of rank one, then
![]() $\boldsymbol F_2$
would be amenable by Corollary 2.11(ii), which is a contradiction. This argument works also for each non-amenable residually finite group in place of
$\boldsymbol F_2$
would be amenable by Corollary 2.11(ii), which is a contradiction. This argument works also for each non-amenable residually finite group in place of
![]() $\boldsymbol F_2$
.
$\boldsymbol F_2$
.
We also provide two examples of non-rank-one odometer actions for amenable groups G. In the first example, G is locally finite, and in the second one, G is non-locally finite periodic.
Example 4.5. Let
![]() $Z=\{0,1\}^{\mathbb {N}}$
. Endow Z with the infinite product
$Z=\{0,1\}^{\mathbb {N}}$
. Endow Z with the infinite product
![]() $\eta $
of the equidistributions on
$\eta $
of the equidistributions on
![]() $\{0,1\}$
. Fix a sequence
$\{0,1\}$
. Fix a sequence
![]() $\boldsymbol {s}=(s_n)_{n=0}^\infty $
of mappings
$\boldsymbol {s}=(s_n)_{n=0}^\infty $
of mappings
Consider the following transformation
![]() $T_{\boldsymbol {s}}$
of Z:
$T_{\boldsymbol {s}}$
of Z:
Of course,
![]() $T_{\boldsymbol {s}}$
preserves
$T_{\boldsymbol {s}}$
preserves
![]() $\eta $
. Let
$\eta $
. Let
Then, G is a locally finite (and hence amenable) countable group. We claim that the dynamical system
![]() $(Z,\eta , G)$
is a G-odometer. Indeed, for each
$(Z,\eta , G)$
is a G-odometer. Indeed, for each
![]() $n\in \mathbb N$
, we denote by
$n\in \mathbb N$
, we denote by
![]() $\pi _n:Z\to \{0,1\}^{n}$
the projection to the first n coordinates. Of course, there is a natural transitive action of G on
$\pi _n:Z\to \{0,1\}^{n}$
the projection to the first n coordinates. Of course, there is a natural transitive action of G on
![]() $\{0,1\}^{n}$
:
$\{0,1\}^{n}$
:
Then,
![]() $\pi _n$
is a G-equivariant mapping. Thus,
$\pi _n$
is a G-equivariant mapping. Thus,
![]() $\{0,1\}^n$
is a finite factor of
$\{0,1\}^n$
is a finite factor of
![]() $(Z,\eta , G)$
. Let
$(Z,\eta , G)$
. Let
In other words,
![]() $\Gamma _n$
is the stabilizer of a point
$\Gamma _n$
is the stabilizer of a point
![]() $(0,\ldots ,0)\in \{0,1\}^n$
. It is straightforward to verify that
$(0,\ldots ,0)\in \{0,1\}^n$
. It is straightforward to verify that
Hence,
![]() $\Gamma _n$
is a cofinite subgroup in G for each n. Moreover,
$\Gamma _n$
is a cofinite subgroup in G for each n. Moreover, ![]() . Thus, we obtain, for each n, a G-equivariant bijection
. Thus, we obtain, for each n, a G-equivariant bijection
![]() $\phi _n:\{0,1\}^n\to G/\Gamma _n$
such that the following diagram commutes:
$\phi _n:\{0,1\}^n\to G/\Gamma _n$
such that the following diagram commutes:

where
![]() $\tau _n(z_1,\ldots ,z_{n+1}):=(z_1,\ldots ,z_{n})$
for each
$\tau _n(z_1,\ldots ,z_{n+1}):=(z_1,\ldots ,z_{n})$
for each
![]() $(z_1,\ldots ,z_{n+1})\in \{0,1\}^{n+1}$
and all
$(z_1,\ldots ,z_{n+1})\in \{0,1\}^{n+1}$
and all
![]() ${n\in \mathbb N}$
. It is routine to check that
${n\in \mathbb N}$
. It is routine to check that
 $$ \begin{align*} \widetilde\Gamma_n:=\bigcap_{g\in G}g\Gamma_n g^{-1}= \{T_{\boldsymbol{s}}\mid \boldsymbol{s}=(s_k)_{k=0}^\infty\text{ with } s_0=I, s_1\equiv I,s_2\equiv I,\ldots, s_{n-1}\equiv I\} \end{align*} $$
$$ \begin{align*} \widetilde\Gamma_n:=\bigcap_{g\in G}g\Gamma_n g^{-1}= \{T_{\boldsymbol{s}}\mid \boldsymbol{s}=(s_k)_{k=0}^\infty\text{ with } s_0=I, s_1\equiv I,s_2\equiv I,\ldots, s_{n-1}\equiv I\} \end{align*} $$
and
![]() $\bigcap _{n=1}^\infty \widetilde \Gamma _n=\{I\}$
. Denote by
$\bigcap _{n=1}^\infty \widetilde \Gamma _n=\{I\}$
. Denote by
![]() $(Y,O)$
the topological G-odometer associated with the sequence
$(Y,O)$
the topological G-odometer associated with the sequence
![]() $(\Gamma _n)_{n=1}^\infty $
. Furnish it with the Haar measure
$(\Gamma _n)_{n=1}^\infty $
. Furnish it with the Haar measure
![]() $\nu $
. Then, equation (4.5) yields a G-equivariant isomorphism
$\nu $
. Then, equation (4.5) yields a G-equivariant isomorphism
![]() $\phi :(Z,\eta )\to (Y,\nu )$
, as desired.
$\phi :(Z,\eta )\to (Y,\nu )$
, as desired.
We now show that
![]() $(Z,\eta ,G)$
is not free. Take a point
$(Z,\eta ,G)$
is not free. Take a point
![]() $z=(z_n)_{n=1}^\infty \in Z$
. Then, the G-stabilizer
$z=(z_n)_{n=1}^\infty \in Z$
. Then, the G-stabilizer
![]() $G_z$
of z is the group
$G_z$
of z is the group

Let
![]() $r_1:\{0,1\}\to \text {Homeo}(\{0,1\})$
be the only mapping such that
$r_1:\{0,1\}\to \text {Homeo}(\{0,1\})$
be the only mapping such that
![]() $r_1(z_1)=I$
but
$r_1(z_1)=I$
but
![]() $r_1\not \equiv I$
. We define a transformation R of
$r_1\not \equiv I$
. We define a transformation R of
![]() $(Z,\eta )$
by setting
$(Z,\eta )$
by setting
Then,
![]() $G_z\ni R\ne I$
. Hence, O is not free. Therefore, O is not of rank one.
$G_z\ni R\ne I$
. Hence, O is not free. Therefore, O is not of rank one.
Example 4.6. Let
![]() $(Z,\eta )$
and
$(Z,\eta )$
and
![]() $\pi _n$
be as in Example 4.5. Denote by
$\pi _n$
be as in Example 4.5. Denote by
![]() $\mathcal R$
the tail equivalence relation on Z. We let
$\mathcal R$
the tail equivalence relation on Z. We let
Then,
![]() ${ \mathcal A}$
is a subgroup of
${ \mathcal A}$
is a subgroup of
![]() $[\mathcal R]$
. Of course,
$[\mathcal R]$
. Of course,
![]() ${ \mathcal A}$
generates
${ \mathcal A}$
generates
![]() $\mathcal R$
. Let
$\mathcal R$
. Let
![]() $\theta $
denote the non-identity bijection of
$\theta $
denote the non-identity bijection of
![]() $\{0,1\}$
. Define four transformations
$\{0,1\}$
. Define four transformations
![]() $a,b,c,d\in \mathcal A$
by the following formulae:
$a,b,c,d\in \mathcal A$
by the following formulae:
 $$ \begin{align*} \begin{aligned} a(z_1,z_2,\ldots) &:=(\theta(z_1),z_2,\ldots),\\ b(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}, \end{cases} \\ c(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 1+3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}, \end{cases} \\ d(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 2+3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}. \end{cases} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} a(z_1,z_2,\ldots) &:=(\theta(z_1),z_2,\ldots),\\ b(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}, \end{cases} \\ c(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 1+3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}, \end{cases} \\ d(1^n,0,z_{n+2},\ldots)&:= \begin{cases} (1^n,0,\theta(z_{n+2}),z_{n+3},\ldots) &\text{if }n\not\in 2+3{\mathbb Z}_+,\\ (1^n,0,z_{n+2},z_{n+3},\ldots) &\text{otherwise}. \end{cases} \end{aligned} \end{align*} $$
We remind that the group G generated by
![]() $a,b,c,d$
is called the Grigorchuk group. It was introduced in [Reference GrigorchukGri]. The group is residually finite, amenable, non-locally finite. Every proper quotient subgroup of G is finite. Of course,
$a,b,c,d$
is called the Grigorchuk group. It was introduced in [Reference GrigorchukGri]. The group is residually finite, amenable, non-locally finite. Every proper quotient subgroup of G is finite. Of course,
![]() $G\subset {\mathcal A}$
. It is routine to verify
$G\subset {\mathcal A}$
. It is routine to verify
![]() $\mathcal R$
is the G-orbit equivalence relation. Hence, G is an ergodic transformation group of
$\mathcal R$
is the G-orbit equivalence relation. Hence, G is an ergodic transformation group of
![]() $(Z,\eta )$
. Since
$(Z,\eta )$
. Since
![]() $\pi _n$
is a G-equivariant mapping of Z onto
$\pi _n$
is a G-equivariant mapping of Z onto
![]() $\{0,1\}^n$
and the dynamical system
$\{0,1\}^n$
and the dynamical system
![]() $(Z,\eta , G)$
is ergodic, G acts transitively on
$(Z,\eta , G)$
is ergodic, G acts transitively on
![]() $\{0,1\}^n$
. Therefore, repeating our reasoning in Example 4.5 almost literally, we obtain that
$\{0,1\}^n$
. Therefore, repeating our reasoning in Example 4.5 almost literally, we obtain that
![]() $(Z,\eta , G)$
is isomorphic to the probability preserving G-odometer associated with the following sequence
$(Z,\eta , G)$
is isomorphic to the probability preserving G-odometer associated with the following sequence
![]() $(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups
$(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups
![]() ${\Gamma _n\subset G}$
:
${\Gamma _n\subset G}$
:
and
![]() $\bigcap _{g\in G}\bigcap _{n=1}^\infty g\Gamma _ng^{-1}=\{I\}$
. Furthermore, the stabilizer
$\bigcap _{g\in G}\bigcap _{n=1}^\infty g\Gamma _ng^{-1}=\{I\}$
. Furthermore, the stabilizer
![]() $G_z$
of this odometer at a point
$G_z$
of this odometer at a point
![]() $z=(z_n)_{n=1}^\infty \in Z$
is the group
$z=(z_n)_{n=1}^\infty \in Z$
is the group
Hence, G is not free. Therefore, G is not of rank one.
However, we will show that each probability preserving G-odometer is a factor of a rank-one
![]() $\sigma $
-finite measure preserving G-action.
$\sigma $
-finite measure preserving G-action.
Theorem 4.7. Let
![]() $(Y,O)$
be a topological G-odometer associated with a decreasing sequence
$(Y,O)$
be a topological G-odometer associated with a decreasing sequence ![]() of cofinite subgroups in G satisfying equation (4.1). Then there is a topological
of cofinite subgroups in G satisfying equation (4.1). Then there is a topological
![]() $(C,F)$
-action T of G on a locally compact Cantor space X and a continuous G-equivariant mapping
$(C,F)$
-action T of G on a locally compact Cantor space X and a continuous G-equivariant mapping
![]() $\tau :X\to Y$
. Moreover,
$\tau :X\to Y$
. Moreover,
![]() $\tau $
maps the Haar measure (see Remark 2.5) on X to a (non-
$\tau $
maps the Haar measure (see Remark 2.5) on X to a (non-
![]() $\sigma $
-finite, in general) measure which is equivalent to the Haar measure on Y. (This means that the two measures have the same class of subsets of zero measure.)
$\sigma $
-finite, in general) measure which is equivalent to the Haar measure on Y. (This means that the two measures have the same class of subsets of zero measure.)
Proof. Construct inductively sequences
![]() $(C_n)_{n=1}^\infty $
and
$(C_n)_{n=1}^\infty $
and
![]() $(F_{n})_{n=0}^\infty $
of finite subsets in G such that equations (2.1) and (2.4) hold,
$(F_{n})_{n=0}^\infty $
of finite subsets in G such that equations (2.1) and (2.4) hold,
![]() $C_n\subset \Gamma _n$
and the projection
$C_n\subset \Gamma _n$
and the projection
for each
![]() $n\in \mathbb N$
. Let T be the topological
$n\in \mathbb N$
. Let T be the topological
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $(C_n,F_{n-1})_{n=1}^\infty $
. By Proposition 2.9, T is defined on the entire locally compact space
$(C_n,F_{n-1})_{n=1}^\infty $
. By Proposition 2.9, T is defined on the entire locally compact space
![]() $X=\bigcup _{n=0}^\infty X_n$
, where
$X=\bigcup _{n=0}^\infty X_n$
, where ![]() . We define
. We define
![]() $\tau :X\to Y$
by setting
$\tau :X\to Y$
by setting
if
![]() $x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n$
for some
$x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n$
for some
![]() $n\in X_n$
. Of course,
$n\in X_n$
. Of course,
![]() $\tau $
is well defined, continuous and G-equivariant. Thus, the first claim of the proposition is proved.
$\tau $
is well defined, continuous and G-equivariant. Thus, the first claim of the proposition is proved.
Let
![]() $\mu $
denote the Haar measure on X and let
$\mu $
denote the Haar measure on X and let
![]() $\chi $
be the Haar measure on Y. Then,
$\chi $
be the Haar measure on Y. Then,
![]() $\mu $
is the unique T-invariant
$\mu $
is the unique T-invariant
![]() $(C,F)$
-measure such that
$(C,F)$
-measure such that
![]() $\mu (X_0)=1$
. It is determined by the sequence
$\mu (X_0)=1$
. It is determined by the sequence
![]() $(\kappa _n,\nu _{n-1})_{n=1}^\infty $
, where
$(\kappa _n,\nu _{n-1})_{n=1}^\infty $
, where
![]() $\kappa _n$
is the equidistribution on
$\kappa _n$
is the equidistribution on
![]() $C_n$
, and
$C_n$
, and
![]() $\nu _n(f)=\prod _{k=1}^n\kappa _k(1_G)$
for each
$\nu _n(f)=\prod _{k=1}^n\kappa _k(1_G)$
for each
![]() $f\in F_n$
and
$f\in F_n$
and
![]() $n\in \mathbb N$
. We now show that
$n\in \mathbb N$
. We now show that
![]() $ (\mu \restriction X_0)\circ \tau ^{-1}=\chi. $
Let
$ (\mu \restriction X_0)\circ \tau ^{-1}=\chi. $
Let
![]() $\tau _n$
stand for the mapping
$\tau _n$
stand for the mapping
We note that if
for some
![]() $c_1,c_1'\in C_1,\ldots ,c_n,c_n'\in C_n$
, then
$c_1,c_1'\in C_1,\ldots ,c_n,c_n'\in C_n$
, then
![]() $c_j=c_j'$
for each
$c_j=c_j'$
for each
![]() $j=1,\ldots ,n$
. Indeed,
$j=1,\ldots ,n$
. Indeed,
Therefore, equation (4.6) yields that
![]() $c_1=c_1'$
and hence
$c_1=c_1'$
and hence ![]() . Arguing in a similar way, we obtain that
. Arguing in a similar way, we obtain that
![]() $c_2=c_2', \ldots , c_n=c_n'$
, as claimed. It follows that
$c_2=c_2', \ldots , c_n=c_n'$
, as claimed. It follows that
![]() $\tau _n$
is one-to-one. Moreover,
$\tau _n$
is one-to-one. Moreover,
![]() $\tau _n$
is onto in view of equation (4.5). Then it is straightforward to verify that the diagram
$\tau _n$
is onto in view of equation (4.5). Then it is straightforward to verify that the diagram

commutes. Passing to the projective limit, we obtain that
![]() $\tau $
is a homeomorphism of
$\tau $
is a homeomorphism of
![]() $X_0$
onto Y. Since
$X_0$
onto Y. Since
![]() $\tau _n$
maps the equidistribution on
$\tau _n$
maps the equidistribution on ![]() to the equidistribution on
to the equidistribution on
![]() $G/\Gamma _{n+1}$
for each n, it follows that
$G/\Gamma _{n+1}$
for each n, it follows that
![]() $\tau $
maps
$\tau $
maps
![]() $\mu \restriction X_0$
to
$\mu \restriction X_0$
to
![]() $\chi $
. Take a probability measure
$\chi $
. Take a probability measure
![]() $\mu '$
on X which is equivalent to
$\mu '$
on X which is equivalent to
![]() $\mu $
. Then,
$\mu $
. Then,
Since
![]() $\mu '$
is quasi-invariant and ergodic under T, it follows that
$\mu '$
is quasi-invariant and ergodic under T, it follows that
![]() $\mu '\circ \tau ^{-1}$
is quasi-invariant and ergodic under O. As the two probability Borel measures
$\mu '\circ \tau ^{-1}$
is quasi-invariant and ergodic under O. As the two probability Borel measures
![]() $\mu '\circ \tau ^{-1}$
and
$\mu '\circ \tau ^{-1}$
and
![]() $\chi $
on Y are quasi-invariant and ergodic under O, they are either equivalent or mutually singular. Therefore, equation (4.7) yields that
$\chi $
on Y are quasi-invariant and ergodic under O, they are either equivalent or mutually singular. Therefore, equation (4.7) yields that
![]() $\mu '\circ \tau ^{-1}\sim \chi $
. Hence,
$\mu '\circ \tau ^{-1}\sim \chi $
. Hence,
![]() $\mu \circ \tau ^{-1}$
is equivalent to
$\mu \circ \tau ^{-1}$
is equivalent to
![]() $\chi $
, as desired.
$\chi $
, as desired.
Remark 4.8. If we change the construction of T in the proof of Theorem 4.7 in such a way that the mapping in equation (4.6) is one-to-one but
![]() $\# (C_n)/\#(\Gamma _n/\Gamma _{n+1})\le 0.5 $
for each
$\# (C_n)/\#(\Gamma _n/\Gamma _{n+1})\le 0.5 $
for each
![]() $n\in \mathbb N$
, then the first claim of Theorem 4.7 still holds: there is a G-equivariant continuous mapping
$n\in \mathbb N$
, then the first claim of Theorem 4.7 still holds: there is a G-equivariant continuous mapping
![]() $\tau :X\to Y$
. However, the second claim fails: the O-quasi-invariant measure
$\tau :X\to Y$
. However, the second claim fails: the O-quasi-invariant measure
![]() ${\mu \circ \tau ^{-1}}$
on Y will be singular with
${\mu \circ \tau ^{-1}}$
on Y will be singular with
![]() $\chi $
.
$\chi $
.
We note that if G is Abelian, then each ergodic non-singular G-action T possesses the following property. Let ![]() be a sequence of cofinite subgroups in G with
be a sequence of cofinite subgroups in G with
![]() $\bigcap _{n\in \mathbb N}\Gamma _n=\{1_G\}$
. If, for each
$\bigcap _{n\in \mathbb N}\Gamma _n=\{1_G\}$
. If, for each
![]() $n\in \mathbb N$
, T has a finite factor
$n\in \mathbb N$
, T has a finite factor ![]() isomorphic to the homogeneous G-space
isomorphic to the homogeneous G-space
![]() $G/\Gamma _n$
, then
$G/\Gamma _n$
, then ![]() and T has an odometer factor
and T has an odometer factor ![]() . This is no longer true if G is non-Abelian (see Example 3.5). However, the following version of the aforementioned property holds for an arbitrary G.
. This is no longer true if G is non-Abelian (see Example 3.5). However, the following version of the aforementioned property holds for an arbitrary G.
Theorem 4.9. Let
![]() $T=(T_g)_{g\in G}$
be an ergodic non-singular G-action on a standard non-atomic probability space
$T=(T_g)_{g\in G}$
be an ergodic non-singular G-action on a standard non-atomic probability space ![]() . Let
. Let ![]() be a sequence of cofinite subgroups in G such that equation (4.1) holds. Denote by
be a sequence of cofinite subgroups in G such that equation (4.1) holds. Denote by
![]() $(Y,O)$
the topological G-odometer associated with this sequence. Suppose that for each
$(Y,O)$
the topological G-odometer associated with this sequence. Suppose that for each
![]() $n\in \mathbb N$
, there exists a T-factor which is isomorphic to the homogeneous G-space
$n\in \mathbb N$
, there exists a T-factor which is isomorphic to the homogeneous G-space
![]() $G/\Gamma _n$
. Then there is an O-quasi-invariant measure
$G/\Gamma _n$
. Then there is an O-quasi-invariant measure
![]() $\nu $
on Y such that the non-singular odometer
$\nu $
on Y such that the non-singular odometer
![]() $(Y,\nu ,O)$
is a factor of
$(Y,\nu ,O)$
is a factor of
![]() $(X,\mu ,T)$
.
$(X,\mu ,T)$
.
Proof. We first prove an auxiliary claim.
Claim A. Let H be a cofinite subgroup in G. There exist no more than
![]() $\# (G/H)$
different factors of T that are isomorphic to the homogeneous G-space
$\# (G/H)$
different factors of T that are isomorphic to the homogeneous G-space
![]() $G/H$
.
$G/H$
.
Proof. Let
![]() $J:=\# (G/H)+1$
. Suppose that there are J pairwise different T-invariant
$J:=\# (G/H)+1$
. Suppose that there are J pairwise different T-invariant
![]() $\sigma $
-algebras
$\sigma $
-algebras ![]() such that
such that ![]() is isomorphic to
is isomorphic to
![]() $G/H$
for each
$G/H$
for each
![]() $j\in J$
. Denote by
$j\in J$
. Denote by
![]() $\tau _j:X\to G/H$
the corresponding G-equivariant mapping. Then the mapping
$\tau _j:X\to G/H$
the corresponding G-equivariant mapping. Then the mapping
is also G-equivariant. Denote by E the support of the measure
![]() $\mu \circ \tau ^{-1}$
. Then:
$\mu \circ \tau ^{-1}$
. Then:
-
• E is a single G-orbit;
-
• the projection of E onto each of the J coordinates is onto.
Take a point
![]() $(g_jH)_{j\in J}\in E$
. Since
$(g_jH)_{j\in J}\in E$
. Since
![]() $J>\#(G/H)$
, there are
$J>\#(G/H)$
, there are
![]() $i_0, j_0\in J$
such that
$i_0, j_0\in J$
such that
![]() $i_0\ne j_0$
but
$i_0\ne j_0$
but
![]() $g_{i_0}H=g_{j_0}H$
. Hence, the projection of E onto the ‘plane’ generated by the
$g_{i_0}H=g_{j_0}H$
. Hence, the projection of E onto the ‘plane’ generated by the
![]() $i_0$
and
$i_0$
and
![]() $j_0$
coordinates is the diagonal
$j_0$
coordinates is the diagonal
![]() $\{(gH,gH)\mid g\in G\}$
in
$\{(gH,gH)\mid g\in G\}$
in
![]() $(G/H)^2$
. Hence,
$(G/H)^2$
. Hence, ![]() . This contradiction proves Claim A.
. This contradiction proves Claim A.
To prove the theorem, we define a graded graph
![]() $\mathcal G$
. The set V of vertices of
$\mathcal G$
. The set V of vertices of
![]() $\mathcal G$
is the union
$\mathcal G$
is the union
![]() $\bigsqcup _{n\ge 0}V_n$
, where
$\bigsqcup _{n\ge 0}V_n$
, where
![]() $V_n$
is the set of all Borel G-equivariant maps from X to
$V_n$
is the set of all Borel G-equivariant maps from X to
![]() $G/\Gamma _n$
. For the consistency of notation, we let
$G/\Gamma _n$
. For the consistency of notation, we let
![]() $\Gamma _0:=G$
. Given
$\Gamma _0:=G$
. Given
![]() $n\ge 0$
, we denote by
$n\ge 0$
, we denote by
![]() $\theta _n$
the projection
$\theta _n$
the projection
The set E of edges of
![]() $\mathcal G$
is the union
$\mathcal G$
is the union
![]() $\bigsqcup _{n\ge 0}E_n$
, where an edge
$\bigsqcup _{n\ge 0}E_n$
, where an edge
![]() $e\in E_n$
joins a vertex
$e\in E_n$
joins a vertex
![]() $\pi \in V_n$
with a vertex
$\pi \in V_n$
with a vertex
![]() $\tau \in V_{n+1}$
if
$\tau \in V_{n+1}$
if
![]() $\pi =\theta _n\circ \tau $
. It follows from Claim A that
$\pi =\theta _n\circ \tau $
. It follows from Claim A that
![]() $V_n$
is finite for each n. Of course, every vertex from
$V_n$
is finite for each n. Of course, every vertex from
![]() $V_n$
is adjacent (that is, connected by an edge) with a vertex in
$V_n$
is adjacent (that is, connected by an edge) with a vertex in
![]() $V_{n-1}$
for each
$V_{n-1}$
for each
![]() $n\in \mathbb N$
. Hence, for each vertex of
$n\in \mathbb N$
. Hence, for each vertex of
![]() $\mathcal G$
, there is a path connecting this vertex with the only vertex from
$\mathcal G$
, there is a path connecting this vertex with the only vertex from
![]() $V_0$
. Thus,
$V_0$
. Thus,
![]() $\mathcal G$
is connected. Of course,
$\mathcal G$
is connected. Of course,
![]() $\mathcal G$
is locally finite and infinite. Hence, by Kőnig’s infinity lemma,
$\mathcal G$
is locally finite and infinite. Hence, by Kőnig’s infinity lemma,
![]() $\mathcal G$
contains a ray. It follows that there exists a Borel G-equivariant mapping
$\mathcal G$
contains a ray. It follows that there exists a Borel G-equivariant mapping
![]() $\iota :X\to Y$
. We set
$\iota :X\to Y$
. We set
![]() $\nu :=\mu \circ \iota ^{-1}$
. Then,
$\nu :=\mu \circ \iota ^{-1}$
. Then,
![]() $(Y,\nu ,O)$
is a factor of
$(Y,\nu ,O)$
is a factor of
![]() $(X,\mu ,T)$
, as desired.
$(X,\mu ,T)$
, as desired.
4.2. Normal covers for non-singular odometers
Let
![]() $(Y,O)$
be a topological G-odometer associated with a decreasing sequence
$(Y,O)$
be a topological G-odometer associated with a decreasing sequence
![]() $(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G such that equation (4.1) holds. If each
$(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G such that equation (4.1) holds. If each
![]() $\Gamma _n$
is normal in G, then
$\Gamma _n$
is normal in G, then
![]() $(Y,O)$
is called normal. In this case, we have that
$(Y,O)$
is called normal. In this case, we have that
![]() $G/\Gamma _n$
is a finite group and hence Y is a compact totally disconnected metric group. Moreover, there is a one-to-one group homomorphism
$G/\Gamma _n$
is a finite group and hence Y is a compact totally disconnected metric group. Moreover, there is a one-to-one group homomorphism
![]() $\phi :G\to Y$
such that
$\phi :G\to Y$
such that
![]() $O_gy=\phi (g)y$
for all
$O_gy=\phi (g)y$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $y\in Y$
. Of course,
$y\in Y$
. Of course,
![]() $\phi (g)=(g\Gamma _1,g\Gamma _2,\ldots )\in Y$
for each
$\phi (g)=(g\Gamma _1,g\Gamma _2,\ldots )\in Y$
for each
![]() $g\in G$
. This homomorphism embeds G densely into Y. Every normal odometer is free.
$g\in G$
. This homomorphism embeds G densely into Y. Every normal odometer is free.
Given a cofinite subgroup
![]() $\Gamma $
in G, the subgroup
$\Gamma $
in G, the subgroup
![]() $\widetilde \Gamma :=\bigcap _{g\in G}g\Gamma g^{-1}$
is the maximal normal (in G) subgroup of
$\widetilde \Gamma :=\bigcap _{g\in G}g\Gamma g^{-1}$
is the maximal normal (in G) subgroup of
![]() $\Gamma $
. Of course,
$\Gamma $
. Of course,
![]() $\widetilde \Gamma $
is of finite index in G. The natural projection
$\widetilde \Gamma $
is of finite index in G. The natural projection
![]() $G/\widetilde \Gamma \ni g\widetilde \Gamma \mapsto g\Gamma \in G/\Gamma $
is G-equivariant. Hence, for a decreasing sequence
$G/\widetilde \Gamma \ni g\widetilde \Gamma \mapsto g\Gamma \in G/\Gamma $
is G-equivariant. Hence, for a decreasing sequence ![]() of cofinite subgroups in G satisfying equation (4.1), we obtain a decreasing sequence
of cofinite subgroups in G satisfying equation (4.1), we obtain a decreasing sequence ![]() of normal cofinite subgroups in G with
of normal cofinite subgroups in G with
![]() $\bigcap _{n=1}^\infty \widetilde \Gamma _n=\{1_G\}$
. Let
$\bigcap _{n=1}^\infty \widetilde \Gamma _n=\{1_G\}$
. Let
![]() $(\widetilde Y, \widetilde O)$
denote the normal topological G-odometer associated with
$(\widetilde Y, \widetilde O)$
denote the normal topological G-odometer associated with
![]() $(\widetilde \Gamma _n)_{n=1}^\infty $
. It is called the topological normal cover of
$(\widetilde \Gamma _n)_{n=1}^\infty $
. It is called the topological normal cover of
![]() $(Y,O)$
. The natural projections
$(Y,O)$
. The natural projections
generate a continuous projection
![]() $w:\widetilde Y\to Y$
that intertwines
$w:\widetilde Y\to Y$
that intertwines
![]() $\widetilde O$
with O. Let
$\widetilde O$
with O. Let
Then, H is a closed subgroup of
![]() $\widetilde Y$
. We claim that
$\widetilde Y$
. We claim that
![]() $\omega $
is the quotient mapping
$\omega $
is the quotient mapping
Indeed, we first observe that
![]() $\omega (\widetilde y)=\omega (\widetilde yh)$
for all
$\omega (\widetilde y)=\omega (\widetilde yh)$
for all
![]() $\widetilde y\in \widetilde Y$
and
$\widetilde y\in \widetilde Y$
and
![]() $h\in H$
. Second, if
$h\in H$
. Second, if
![]() ${\omega (\widetilde y)=\omega (\widetilde z)}$
for some
${\omega (\widetilde y)=\omega (\widetilde z)}$
for some
![]() $\widetilde y,\widetilde z\in \widetilde Y$
, then
$\widetilde y,\widetilde z\in \widetilde Y$
, then
![]() $\widetilde y\widetilde z^{-1}\in H$
. Finally, the subset
$\widetilde y\widetilde z^{-1}\in H$
. Finally, the subset
![]() $\omega (\widetilde Y)$
is G-invariant and closed in Y. Hence,
$\omega (\widetilde Y)$
is G-invariant and closed in Y. Hence,
![]() $\omega (\widetilde Y)=Y$
.
$\omega (\widetilde Y)=Y$
.
It may seem that the coordinate projection
![]() $H\ni (\widetilde y_n)_{n=1}^\infty \mapsto \widetilde y_n\in \Gamma _n/\widetilde \Gamma _n$
is onto for each
$H\ni (\widetilde y_n)_{n=1}^\infty \mapsto \widetilde y_n\in \Gamma _n/\widetilde \Gamma _n$
is onto for each
![]() $n\in \mathbb N$
. That is not true. A counterexample (in which H is trivial but
$n\in \mathbb N$
. That is not true. A counterexample (in which H is trivial but
![]() $\#(\Gamma _n/\widetilde \Gamma _n)=2$
for each n) is constructed in Example 6.7 below.
$\#(\Gamma _n/\widetilde \Gamma _n)=2$
for each n) is constructed in Example 6.7 below.
The concepts of the topological normal cover and the normal cover in the finite measure preserving case can be found in [Reference Cortez and PetiteCorPe, Reference Danilenko and LemańczykDaLe]. We adapt it to the non-singular case in the following way.
Definition 4.10. Let
![]() $(Y,\nu , O)$
be a non-singular G-odometer,
$(Y,\nu , O)$
be a non-singular G-odometer,
![]() $(\widetilde Y,\widetilde O)$
the topological normal cover of
$(\widetilde Y,\widetilde O)$
the topological normal cover of
![]() $(Y,O)$
and
$(Y,O)$
and
![]() $\widetilde \nu $
an
$\widetilde \nu $
an
![]() $\widetilde O$
-quasi-invariant probability on
$\widetilde O$
-quasi-invariant probability on
![]() $\widetilde Y$
. We call the non-singular normal odometer
$\widetilde Y$
. We call the non-singular normal odometer
![]() $(\widetilde Y,\widetilde \nu ,\widetilde O)$
the normal cover of
$(\widetilde Y,\widetilde \nu ,\widetilde O)$
the normal cover of
![]() $(Y,\nu ,O)$
if:
$(Y,\nu ,O)$
if:
-
(i)
 $\widetilde \nu \circ \omega ^{-1}=\nu $
; and
$\widetilde \nu \circ \omega ^{-1}=\nu $
; and -
(ii)
 ${d\widetilde \nu \circ \widetilde O_g}/{d\widetilde \nu }=({d\nu \circ O_g}/{d\nu })\circ \omega $
for each
${d\widetilde \nu \circ \widetilde O_g}/{d\widetilde \nu }=({d\nu \circ O_g}/{d\nu })\circ \omega $
for each
 $g\in G$
.
$g\in G$
.
We note that property (ii) means that
![]() $\widetilde O$
is
$\widetilde O$
is
![]() $\omega $
-relatively finite measure preserving.
$\omega $
-relatively finite measure preserving.
Proposition 4.11. Given a non-singular G-odometer
![]() $(Y,\nu ,O)$
, there is a G-quasi-invariant probability
$(Y,\nu ,O)$
, there is a G-quasi-invariant probability
![]() $\widetilde \nu $
on
$\widetilde \nu $
on
![]() $\widetilde Y$
such that
$\widetilde Y$
such that
![]() $(\widetilde Y,\widetilde \nu ,\widetilde O)$
is a normal cover of
$(\widetilde Y,\widetilde \nu ,\widetilde O)$
is a normal cover of
![]() $(Y,\nu ,O)$
.
$(Y,\nu ,O)$
.
Proof. Without loss of generality, we may assume that
![]() $\widetilde Y=Y\times H$
(as a set, not as a group) and there is a Borel map (1-cocycle)
$\widetilde Y=Y\times H$
(as a set, not as a group) and there is a Borel map (1-cocycle)
![]() $s:G\times Y\to H$
such that
$s:G\times Y\to H$
such that
Denote by
![]() $\unicode{x3bb} _H$
the Haar measure on H. Then the direct product
$\unicode{x3bb} _H$
the Haar measure on H. Then the direct product
![]() $\widetilde \nu :=\nu \otimes \unicode{x3bb} _H$
satisfies properties (i) and (ii) from Definition 4.10.
$\widetilde \nu :=\nu \otimes \unicode{x3bb} _H$
satisfies properties (i) and (ii) from Definition 4.10.
Let ![]() be as above. Suppose that there is a sequence
be as above. Suppose that there is a sequence
![]() $(b_n)_{n=1}^\infty $
of G-elements such that
$(b_n)_{n=1}^\infty $
of G-elements such that
Denote by
![]() $(Y', O')$
the topological odometer associated with this sequence. Let
$(Y', O')$
the topological odometer associated with this sequence. Let
![]() $\nu $
and
$\nu $
and
![]() $\nu '$
stand for the Haar measures on Y and
$\nu '$
stand for the Haar measures on Y and
![]() $Y'$
, respectively.
$Y'$
, respectively.
Proposition 4.12. The odometers
![]() $(Y',O',\nu ')$
and
$(Y',O',\nu ')$
and
![]() $( Y, O,\nu )$
are isomorphic.
$( Y, O,\nu )$
are isomorphic.
Proof. It is easy to see that the normal covers of
![]() $(Y',O',\nu ')$
and
$(Y',O',\nu ')$
and
![]() $( Y, O,\nu )$
are the same. Denote this common normal cover by
$( Y, O,\nu )$
are the same. Denote this common normal cover by
![]() $(\widetilde Y,\widetilde \nu ,\widetilde O)$
. Then there are closed subgroups H and
$(\widetilde Y,\widetilde \nu ,\widetilde O)$
. Then there are closed subgroups H and
![]() $H'$
of
$H'$
of
![]() $\widetilde Y$
such that
$\widetilde Y$
such that
![]() $( Y, O,\nu )$
is the right H-quotient of
$( Y, O,\nu )$
is the right H-quotient of
![]() $(\widetilde Y,\widetilde \nu ,\widetilde O)$
and
$(\widetilde Y,\widetilde \nu ,\widetilde O)$
and
![]() $( Y', O',\nu ')$
is the right
$( Y', O',\nu ')$
is the right
![]() $H'$
-quotient of
$H'$
-quotient of
![]() $(\widetilde Y,\widetilde \nu ,\widetilde O)$
. It follows from Theorem 4.9 that
$(\widetilde Y,\widetilde \nu ,\widetilde O)$
. It follows from Theorem 4.9 that
![]() $(Y',O',\nu ')$
and
$(Y',O',\nu ')$
and
![]() $( Y, O,\nu )$
are weakly equivalent, that is,
$( Y, O,\nu )$
are weakly equivalent, that is,
![]() $(Y',O',\nu ')$
is a factor of
$(Y',O',\nu ')$
is a factor of
![]() $( Y, O,\nu )$
and
$( Y, O,\nu )$
and
![]() $( Y, O,\nu )$
is a factor of
$( Y, O,\nu )$
is a factor of
![]() $(Y',O',\nu ')$
. Hence, there are compact subgroups K and
$(Y',O',\nu ')$
. Hence, there are compact subgroups K and
![]() $K'$
of
$K'$
of
![]() $\widetilde Y$
and elements
$\widetilde Y$
and elements
![]() $a,b\in \widetilde Y$
such that
$a,b\in \widetilde Y$
such that
![]() $K\supset H$
,
$K\supset H$
,
![]() $K'\supset H'$
,
$K'\supset H'$
,
![]() $K=aH'a^{-1}$
and
$K=aH'a^{-1}$
and
![]() $K'=bHb^{-1}$
. Hence,
$K'=bHb^{-1}$
. Hence,
![]() $H\subset abHb^{-1}a^{-1}$
. We claim that this implies that
$H\subset abHb^{-1}a^{-1}$
. We claim that this implies that
![]() $H=abHb^{-1}a^{-1}$
. Indeed, let
$H=abHb^{-1}a^{-1}$
. Indeed, let
![]() $V:=\{y\in \widetilde Y\mid H\subset yHy^{-1}\}$
. Then V is a closed subset of
$V:=\{y\in \widetilde Y\mid H\subset yHy^{-1}\}$
. Then V is a closed subset of
![]() $\widetilde Y$
. Of course,
$\widetilde Y$
. Of course,
![]() $V\ni (ab)^n$
for each
$V\ni (ab)^n$
for each
![]() $n\in \mathbb N$
. Hence, V includes the closure of the semigroup
$n\in \mathbb N$
. Hence, V includes the closure of the semigroup
![]() $\{(ab)^n\mid n\in \mathbb N\}$
. It follows from [Reference Hewitt and RossHeRo, Theorem 9.1] that the closure of
$\{(ab)^n\mid n\in \mathbb N\}$
. It follows from [Reference Hewitt and RossHeRo, Theorem 9.1] that the closure of
![]() $\{(ab)^n\mid n\in \mathbb N\}$
equals the closure of the group
$\{(ab)^n\mid n\in \mathbb N\}$
equals the closure of the group
![]() $\{(ab)^n\mid n\in {\mathbb Z}\}$
. Hence,
$\{(ab)^n\mid n\in {\mathbb Z}\}$
. Hence,
![]() $(ab)^{-1}\in V$
, that is,
$(ab)^{-1}\in V$
, that is,
![]() $H\supset abHb^{-1}a^{-1}$
. Therefore,
$H\supset abHb^{-1}a^{-1}$
. Therefore,
![]() $H=abHb^{-1}a^{-1}$
, as claimed. This yields that
$H=abHb^{-1}a^{-1}$
, as claimed. This yields that
![]() $K= H$
and
$K= H$
and
![]() $K'=H'$
. Thus, we obtain that H and
$K'=H'$
. Thus, we obtain that H and
![]() $H'$
are conjugate. Hence,
$H'$
are conjugate. Hence,
![]() $(Y',O',\nu ')$
and
$(Y',O',\nu ')$
and
![]() $( Y, O,\nu )$
are isomorphic.
$( Y, O,\nu )$
are isomorphic.
5. Odometer factors of non-singular
 $(C,F)$
-actions
$(C,F)$
-actions
The following concept is an ‘infinite’ analogue of Definition 3.1.
Definition 5.1. Let a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii), and let a sequence
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii), and let a sequence
![]() $(\Gamma _n)_{n=1}^\infty $
satisfy equation (4.1). Denote by
$(\Gamma _n)_{n=1}^\infty $
satisfy equation (4.1). Denote by
![]() $(Y,O)$
the topological odometer associated with
$(Y,O)$
the topological odometer associated with
![]() $(\Gamma _n)_{n=1}^\infty $
. Given
$(\Gamma _n)_{n=1}^\infty $
. Given
![]() $y=(g_n\Gamma _n)_{n=1}^\infty \in Y$
, we say that
$y=(g_n\Gamma _n)_{n=1}^\infty \in Y$
, we say that
![]() $\mathcal T$
is compatible with y if
$\mathcal T$
is compatible with y if
 $$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g_n\Gamma_n g_n^{-1}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty\kappa_n (\{c\in C_n\mid c\not\in g_n\Gamma_n g_n^{-1}\})<\infty. \end{align*} $$
Denote by T the
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\mathcal T$
. Let X be the space of T and let
$\mathcal T$
. Let X be the space of T and let
![]() $\mu $
stand for the non-singular
$\mu $
stand for the non-singular
![]() $(C,F)$
-measure on X determined by
$(C,F)$
-measure on X determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _n)_{n=0}^\infty $
. As
$(\nu _n)_{n=0}^\infty $
. As
it follows that if
![]() $\mathcal T$
is compatible with y, then
$\mathcal T$
is compatible with y, then
![]() $\mathcal T$
is compatible with the coset
$\mathcal T$
is compatible with the coset
![]() $g_n\Gamma _n\in G/\Gamma _n$
in the sense of Definition 3.1 for each
$g_n\Gamma _n\in G/\Gamma _n$
in the sense of Definition 3.1 for each
![]() $n\in \mathbb N$
. Hence, the
$n\in \mathbb N$
. Hence, the
![]() $( {\mathcal T},g_n\Gamma _n)$
-factor mapping
$( {\mathcal T},g_n\Gamma _n)$
-factor mapping
![]() $\pi _{({\mathcal T},g_n\Gamma _n)}:X\to G/\Gamma _n$
for T is well defined (mod 0) for each
$\pi _{({\mathcal T},g_n\Gamma _n)}:X\to G/\Gamma _n$
for T is well defined (mod 0) for each
![]() $n\in \mathbb N$
. Moreover, a measurable mapping
$n\in \mathbb N$
. Moreover, a measurable mapping
is well defined (mod 0) too. Of course,
![]() $\pi _{({\mathcal T},y)}\circ T_g=O_g\circ \pi _{({\mathcal T},y)}$
for each
$\pi _{({\mathcal T},y)}\circ T_g=O_g\circ \pi _{({\mathcal T},y)}$
for each
![]() $g\in G$
. Hence, the non-singular odometer
$g\in G$
. Hence, the non-singular odometer
![]() $(Y,\mu \circ \pi _{({\mathcal T},y)}^{-1}, O)$
is a factor of
$(Y,\mu \circ \pi _{({\mathcal T},y)}^{-1}, O)$
is a factor of
![]() $(X,\mu , T)$
.
$(X,\mu , T)$
.
Definition 5.2. We call
![]() $\pi _{({\mathcal T},y)}$
the
$\pi _{({\mathcal T},y)}$
the
![]() $({\mathcal T},y)$
-factor mapping for T.
$({\mathcal T},y)$
-factor mapping for T.
In the proposition below, we find necessary and sufficient conditions (in terms of the parameters
![]() $\mathcal T$
) under which
$\mathcal T$
) under which
![]() $\pi _{({\mathcal T},y)}$
is one-to-one, that is, the dynamical systems
$\pi _{({\mathcal T},y)}$
is one-to-one, that is, the dynamical systems
![]() $(X,\mu ,T)$
and
$(X,\mu ,T)$
and
![]() $(Y,\mu \circ \pi _{({\mathcal T},y)}^{-1},O)$
are isomorphic via
$(Y,\mu \circ \pi _{({\mathcal T},y)}^{-1},O)$
are isomorphic via
![]() $\pi _{({\mathcal T},y)}$
.
$\pi _{({\mathcal T},y)}$
.
Proposition 5.3. Let
![]() $\mathcal T$
be compatible with y. The following are equivalent:
$\mathcal T$
be compatible with y. The following are equivalent:
-
(i)
 $\pi _{({\mathcal T},y)}$
is one-to-one (mod 0);
$\pi _{({\mathcal T},y)}$
is one-to-one (mod 0); -
(ii) for each
 $n>0$
and
$n>0$
and
 $\epsilon>0$
, there are
$\epsilon>0$
, there are
 $l>0$
and a subset
$l>0$
and a subset
 $D_l\subset G/\Gamma _l$
such that
$D_l\subset G/\Gamma _l$
such that
 $\mu ([1_G]_n\triangle \pi _{({\mathcal T},g_l\Gamma _l)}^{-1}(D_l)) < \epsilon $
; and
$\mu ([1_G]_n\triangle \pi _{({\mathcal T},g_l\Gamma _l)}^{-1}(D_l)) < \epsilon $
; and -
(iii) for each
 $n>0$
and
$n>0$
and
 $\epsilon>0$
, there are
$\epsilon>0$
, there are
 $l>0$
, a subset
$l>0$
, a subset
 $D_l\subset G/\Gamma _l$
and
$D_l\subset G/\Gamma _l$
and
 $M>0$
such that
$M>0$
such that  for each
for each
 $m>M$
.
$m>M$
.
Proof. (i)
![]() $\Leftrightarrow $
(ii) Denote by
$\Leftrightarrow $
(ii) Denote by ![]() and
and ![]() the Borel
the Borel
![]() $\sigma $
-algebra on X and Y, respectively. Of course,
$\sigma $
-algebra on X and Y, respectively. Of course,
![]() $\pi _{({\mathcal T},y)}$
is one-to-one (mod 0) if and only if
$\pi _{({\mathcal T},y)}$
is one-to-one (mod 0) if and only if ![]() (mod 0). Since:
(mod 0). Since:
-
•
 is generated by the family of all cylinders in X; and
is generated by the family of all cylinders in X; and -
•
 is invariant under T,
is invariant under T,
it follows that ![]() if and only if
if and only if ![]() for each
for each
![]() $n>0$
. Let
$n>0$
. Let ![]() denote the finite sub-
denote the finite sub-
![]() $\sigma $
-algebra of subsets that are measurable with respect to the canonical projection
$\sigma $
-algebra of subsets that are measurable with respect to the canonical projection
![]() $G\to G/\Gamma _l$
. Then,
$G\to G/\Gamma _l$
. Then, ![]() and the union
and the union ![]() is dense in
is dense in ![]() . It follows that
. It follows that ![]() if and only if
if and only if
It remains to note that ![]() .
.
(ii)
![]() $\Leftrightarrow $
(iii) We note that for all
$\Leftrightarrow $
(iii) We note that for all
![]() $n>0$
,
$n>0$
,
![]() $l>0$
and a subset
$l>0$
and a subset
![]() $D\subset G/\Gamma _l$
,
$D\subset G/\Gamma _l$
,

The latter follows from the fact that
![]() $\mathcal T$
is compatible with y. It implies that
$\mathcal T$
is compatible with y. It implies that
Hence, for each
![]() $D\subset \Gamma _l$
,
$D\subset \Gamma _l$
,

This equality implies the equivalence of properties (ii) and (iii).
The following theorem is the main result of this section.
Theorem 5.4. Let a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). Let T be the non-singular
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equations (2.1)–(2.3) and Proposition 2.10(ii). Let T be the non-singular
![]() $(C,F)$
-action of G associated with
$(C,F)$
-action of G associated with
![]() $\mathcal T$
and let
$\mathcal T$
and let
![]() $(Y,O)$
be the topological G-odometer associated with a sequence
$(Y,O)$
be the topological G-odometer associated with a sequence
![]() $(\Gamma _n)_{n=1}^\infty $
satisfying equation (4.1). Then, for each G-equivariant measurable mapping
$(\Gamma _n)_{n=1}^\infty $
satisfying equation (4.1). Then, for each G-equivariant measurable mapping
![]() $\tau :X\to Y$
, there exist an increasing sequence
$\tau :X\to Y$
, there exist an increasing sequence
![]() $\boldsymbol q$
of non-negative integers and an element
$\boldsymbol q$
of non-negative integers and an element
![]() $y\in Y$
such that the
$y\in Y$
such that the
![]() $\boldsymbol q$
-telescoping
$\boldsymbol q$
-telescoping
![]() $\widetilde {\mathcal T}= (\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
of
$\widetilde {\mathcal T}= (\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
of
![]() $\mathcal T$
is compatible with y and
$\mathcal T$
is compatible with y and
Moreover,
![]() $\tau $
is one-to-one (mod 0) if and only if for each
$\tau $
is one-to-one (mod 0) if and only if for each
![]() $n>0$
and
$n>0$
and
![]() $\epsilon>0$
, there are
$\epsilon>0$
, there are
![]() $l>0$
, a subset
$l>0$
, a subset
![]() $D_l\subset G/\Gamma _l$
and
$D_l\subset G/\Gamma _l$
and
![]() $M>n$
such that for each
$M>n$
such that for each
![]() $m>M$
,
$m>M$
,
We preface the proof of Theorem 5.4 with auxiliary simple but useful facts about factor mappings.
Lemma 5.5. Let
![]() $\Gamma ,\Gamma _1$
be two cofinite subgroups in G and
$\Gamma ,\Gamma _1$
be two cofinite subgroups in G and
![]() $\Gamma _1\subset \Gamma $
. Then:
$\Gamma _1\subset \Gamma $
. Then:
-
(i) if
 $\mathcal T$
is compatible with a coset
$\mathcal T$
is compatible with a coset
 $g\Gamma \in G/\Gamma $
, then for each increasing sequence
$g\Gamma \in G/\Gamma $
, then for each increasing sequence
 $\boldsymbol a=(a_n)_{n=0}^\infty $
of non-negative integers with
$\boldsymbol a=(a_n)_{n=0}^\infty $
of non-negative integers with
 $a_0=0$
, the
$a_0=0$
, the
 $\boldsymbol a$
-telescoping
$\boldsymbol a$
-telescoping
 $\widetilde {\mathcal T}$
of
$\widetilde {\mathcal T}$
of
 $\mathcal T$
is also compatible with
$\mathcal T$
is also compatible with
 $g\Gamma $
and (5.2)
$g\Gamma $
and (5.2) $$ \begin{align}\pi_{(\mathcal T,g\Gamma)}=\pi_{(\widetilde {\mathcal T},g\Gamma)}\circ\iota_{\boldsymbol a}; \end{align} $$
$$ \begin{align}\pi_{(\mathcal T,g\Gamma)}=\pi_{(\widetilde {\mathcal T},g\Gamma)}\circ\iota_{\boldsymbol a}; \end{align} $$
-
(ii) if
 $\mathcal T$
is compatible with two cosets
$\mathcal T$
is compatible with two cosets
 $g\Gamma \in G/\Gamma $
and
$g\Gamma \in G/\Gamma $
and
 $g_1\Gamma _1\in G/\Gamma _1$
, then
$g_1\Gamma _1\in G/\Gamma _1$
, then  $$ \begin{align*} r\circ \pi_{(\mathcal T,g_1\Gamma_1)}=\pi_{(\mathcal T,g\Gamma)}\quad\text{if and only if } g_1g^{-1}\in\Gamma, \end{align*} $$
$$ \begin{align*} r\circ \pi_{(\mathcal T,g_1\Gamma_1)}=\pi_{(\mathcal T,g\Gamma)}\quad\text{if and only if } g_1g^{-1}\in\Gamma, \end{align*} $$
where
 $r: G/\Gamma _1\to G/\Gamma $
denotes the natural projection.
$r: G/\Gamma _1\to G/\Gamma $
denotes the natural projection.
Proof. (i) For each
![]() $n> 0$
, we let
$n> 0$
, we let ![]() and
and ![]() . Then,
. Then,
 $$ \begin{align*} \widetilde \kappa_n (\{c\in \widetilde C_n\mid c\not\in g \Gamma g^{-1}\})\le \sum_{j=a_{n-1}+1}^{a_{n}}\kappa_j (\{c\in C_j\mid c\not\in g\Gamma g^{-1}\}). \end{align*} $$
$$ \begin{align*} \widetilde \kappa_n (\{c\in \widetilde C_n\mid c\not\in g \Gamma g^{-1}\})\le \sum_{j=a_{n-1}+1}^{a_{n}}\kappa_j (\{c\in C_j\mid c\not\in g\Gamma g^{-1}\}). \end{align*} $$
Hence,
 $$ \begin{align*} \sum_{n=1}^\infty\widetilde \kappa_n (\{c\in \widetilde C_n\mid c\not\in g\Gamma g^{-1}\})\le \sum_{j=1}^\infty\kappa_j (\{c\in C_j\mid c\not\in g\Gamma g^{-1}\})<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty\widetilde \kappa_n (\{c\in \widetilde C_n\mid c\not\in g\Gamma g^{-1}\})\le \sum_{j=1}^\infty\kappa_j (\{c\in C_j\mid c\not\in g\Gamma g^{-1}\})<\infty. \end{align*} $$
Thus,
![]() $\widetilde {\mathcal T}$
is compatible with
$\widetilde {\mathcal T}$
is compatible with
![]() $g\Gamma $
.
$g\Gamma $
.
Equation (5.2) and claim (ii) are verified straightforwardly.
Proof of Theorem 5.4
We note that
![]() $\tau (x)=(\tau _n(x))_{n=1}^\infty $
for each
$\tau (x)=(\tau _n(x))_{n=1}^\infty $
for each
![]() $x\in X$
, where
$x\in X$
, where
![]() $\tau _n:X\to G/\Gamma _n$
is a G-equivariant mapping for every n.
$\tau _n:X\to G/\Gamma _n$
is a G-equivariant mapping for every n.
From now on, we will argue inductively. At the first step we apply Remark 3.4 to T and
![]() $\tau _1$
: there exist a coset
$\tau _1$
: there exist a coset
![]() $g_1\Gamma _1\in G/\Gamma _1$
and an increasing sequence
$g_1\Gamma _1\in G/\Gamma _1$
and an increasing sequence
![]() $\boldsymbol q^1$
of non-negative integers such that the
$\boldsymbol q^1$
of non-negative integers such that the
![]() $\boldsymbol q^1$
-telescoping
$\boldsymbol q^1$
-telescoping
![]() $\mathcal T_1$
of
$\mathcal T_1$
of
![]() $\mathcal T$
is
$\mathcal T$
is
![]() $g_1\Gamma _1$
-compatible and
$g_1\Gamma _1$
-compatible and
At the second step, we apply Remark 3.4 to the
![]() $(C,F)$
-action
$(C,F)$
-action
![]() $ \widetilde T$
of G associated with
$ \widetilde T$
of G associated with
![]() $\mathcal T_1$
and the factor mapping
$\mathcal T_1$
and the factor mapping
![]() $\tau _2\circ {\iota _{\boldsymbol q^1}}^{-1}$
of
$\tau _2\circ {\iota _{\boldsymbol q^1}}^{-1}$
of
![]() $ \widetilde T$
: there exist a coset
$ \widetilde T$
: there exist a coset
![]() $g_2\Gamma _2\in G/\Gamma _2$
and an increasing sequence
$g_2\Gamma _2\in G/\Gamma _2$
and an increasing sequence
![]() $\boldsymbol q^2$
of non-negative integers such that the
$\boldsymbol q^2$
of non-negative integers such that the
![]() $\boldsymbol q^2$
-telescoping
$\boldsymbol q^2$
-telescoping
![]() $\mathcal T_2$
of
$\mathcal T_2$
of
![]() $\mathcal T_1$
is
$\mathcal T_1$
is
![]() $g_2\Gamma _2$
-compatible and
$g_2\Gamma _2$
-compatible and
Consider the natural projection
![]() $\omega _{2,1}:G/\Gamma _2\to G/\Gamma _1$
. Since
$\omega _{2,1}:G/\Gamma _2\to G/\Gamma _1$
. Since
![]() $\omega _{2,1}\circ \tau _2=\tau _1$
, it follows from equations (5.3) and (5.4) that
$\omega _{2,1}\circ \tau _2=\tau _1$
, it follows from equations (5.3) and (5.4) that
Then, Lemma 5.5(i),(ii) imply that
![]() $g_2g_1^{-1}\in \Gamma _1$
. Continuing inductively, we obtain a sequence
$g_2g_1^{-1}\in \Gamma _1$
. Continuing inductively, we obtain a sequence
![]() $(g_n)_{n=1}^\infty $
of elements in G and a sequence
$(g_n)_{n=1}^\infty $
of elements in G and a sequence
![]() $(\boldsymbol q^n)_{n=1}^\infty $
of increasing sequences of non-negative integers such that for each
$(\boldsymbol q^n)_{n=1}^\infty $
of increasing sequences of non-negative integers such that for each
![]() $n>0$
:
$n>0$
:
-
(α1)
 $g_ng_{n-1}^{-1}\in \Gamma _{n-1}$
;
$g_ng_{n-1}^{-1}\in \Gamma _{n-1}$
; -
(α2) the
 $\boldsymbol q^n$
-telescoping
$\boldsymbol q^n$
-telescoping
 $\mathcal T_n=(C_k^{(n)},F_{k-1}^{(n)},\kappa _k^{(n)},\nu _{k-1}^{(n)})_{k=1}^\infty $
of
$\mathcal T_n=(C_k^{(n)},F_{k-1}^{(n)},\kappa _k^{(n)},\nu _{k-1}^{(n)})_{k=1}^\infty $
of
 $\mathcal T_{n-1}$
is compatible with the coset
$\mathcal T_{n-1}$
is compatible with the coset
 $g_{n}\Gamma _n$
; and
$g_{n}\Gamma _n$
; and -
(α3)
 .
.
We now choose an integer
![]() $a_n>0$
large so that:
$a_n>0$
large so that:
-
(α4)
 $\sum _{k\ge a_n}\kappa _k^{(n)}(\{c\in C_k^{(n)}\mid c\not \in g_n\Gamma _n g_n^{-1} \})< 1/{n^2}$
$\sum _{k\ge a_n}\kappa _k^{(n)}(\{c\in C_k^{(n)}\mid c\not \in g_n\Gamma _n g_n^{-1} \})< 1/{n^2}$
for each
![]() $n>0$
. It follows from (
$n>0$
. It follows from (
![]() $\alpha _1$
) that the sequence
$\alpha _1$
) that the sequence
![]() $y:=(g_{n}\Gamma _n)_{n=1}^\infty $
is a well-defined element of Y. Of course:
$y:=(g_{n}\Gamma _n)_{n=1}^\infty $
is a well-defined element of Y. Of course:
-
 $\boldsymbol q^1\circ \boldsymbol q^2$
is a subsequence of
$\boldsymbol q^1\circ \boldsymbol q^2$
is a subsequence of
 $\boldsymbol q^1$
;
$\boldsymbol q^1$
; -
 $\boldsymbol q^1\circ \boldsymbol q^2\circ \boldsymbol q^3$
is a subsequence of
$\boldsymbol q^1\circ \boldsymbol q^2\circ \boldsymbol q^3$
is a subsequence of
 $\boldsymbol q^1\circ \boldsymbol q^2$
$\boldsymbol q^1\circ \boldsymbol q^2$
and so on. Hence, using the diagonalization method, we can construct a sequence
![]() ${\boldsymbol q=(q_n)_{n=1}^\infty }$
of integers such that:
${\boldsymbol q=(q_n)_{n=1}^\infty }$
of integers such that:
-
•
 ;
; -
•
 $\boldsymbol q$
is a subsequence of
$\boldsymbol q$
is a subsequence of  ; and
; and -
•
 $q_n\ge a_n$
$q_n\ge a_n$
for every
![]() $n>0$
. Denote by
$n>0$
. Denote by
![]() $\widetilde {\mathcal T}$
the
$\widetilde {\mathcal T}$
the
![]() $\boldsymbol q$
-telescoping
$\boldsymbol q$
-telescoping
![]() $\widetilde {\mathcal T}=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
of
$\widetilde {\mathcal T}=(\widetilde C_n,\widetilde F_{n-1},\widetilde \kappa _n,\widetilde \nu _{n-1})_{n=1}^\infty $
of
![]() $\mathcal T$
. We are going to show that
$\mathcal T$
. We are going to show that
![]() $\widetilde {\mathcal T}$
is compatible with y. By the construction of
$\widetilde {\mathcal T}$
is compatible with y. By the construction of
![]() $\boldsymbol q$
, for each
$\boldsymbol q$
, for each
![]() $n>0$
, there are integers
$n>0$
, there are integers
![]() $ d_{n,2}\ge d_{n,1}\ge a_n $
such that
$ d_{n,2}\ge d_{n,1}\ge a_n $
such that
Therefore, we deduce from (
![]() $\alpha _4$
) that
$\alpha _4$
) that
 $$ \begin{align*} \widetilde\kappa_n(\{c\in \widetilde C_n\mid c\not\in g_n\Gamma_n g_n^{-1} \}) \le\sum_{k=d_{n,1}}^{d_{n,2}} \kappa_k^{(n)}(\{c\in C_k^{(n)}\mid c\not\in g_n\Gamma_n g_n^{-1} \}) <\frac 1{n^2}. \end{align*} $$
$$ \begin{align*} \widetilde\kappa_n(\{c\in \widetilde C_n\mid c\not\in g_n\Gamma_n g_n^{-1} \}) \le\sum_{k=d_{n,1}}^{d_{n,2}} \kappa_k^{(n)}(\{c\in C_k^{(n)}\mid c\not\in g_n\Gamma_n g_n^{-1} \}) <\frac 1{n^2}. \end{align*} $$
Hence,
![]() $\sum _{n=1}^\infty \widetilde \kappa _n(\{c\in \widetilde C_n\mid c\not \in g_n\Gamma _n g_n^{-1} \})<\infty $
, that is,
$\sum _{n=1}^\infty \widetilde \kappa _n(\{c\in \widetilde C_n\mid c\not \in g_n\Gamma _n g_n^{-1} \})<\infty $
, that is,
![]() $\widetilde {\mathcal T}$
is compatible with y, as desired.
$\widetilde {\mathcal T}$
is compatible with y, as desired.
We now prove equation (5.1). Of course,
![]() $\widetilde {\mathcal T}$
is a telescoping of the
$\widetilde {\mathcal T}$
is a telescoping of the ![]() -telescoping of
-telescoping of
![]() $\mathcal T$
for each n. In view of (
$\mathcal T$
for each n. In view of (
![]() $\alpha _2$
), the
$\alpha _2$
), the ![]() -telescoping of
-telescoping of
![]() $\mathcal T$
equals
$\mathcal T$
equals
![]() $\mathcal T_n$
. Thus,
$\mathcal T_n$
. Thus,
![]() $\widetilde {\mathcal T}$
is a telescoping of
$\widetilde {\mathcal T}$
is a telescoping of
![]() $\mathcal T_n$
. Denote by
$\mathcal T_n$
. Denote by
![]() $\theta _n$
the canonical isomorphism corresponding to this telescoping. Then
$\theta _n$
the canonical isomorphism corresponding to this telescoping. Then ![]() . It follows from this and (
. It follows from this and (
![]() $\alpha _3$
) that
$\alpha _3$
) that
for each
![]() $n\in \mathbb N$
. Hence,
$n\in \mathbb N$
. Hence,
![]() $\pi _{(\widetilde {\mathcal T},y)}=\tau $
, as desired.
$\pi _{(\widetilde {\mathcal T},y)}=\tau $
, as desired.
The second (the last) claim of the theorem follows from the first one and Proposition 5.3.
As a corollary, we obtain a criterion for the existence (or non-existence) of odometer factors for rank-one non-singular actions.
Corollary 5.6. Let T be the non-singular
![]() $(C,F)$
-action of G associated with a sequence
$(C,F)$
-action of G associated with a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then T has no non-singular odometer factors if and only if for each decreasing sequence
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then T has no non-singular odometer factors if and only if for each decreasing sequence ![]() of cofinite subgroups in G satisfying equation (4.1), no telescoping of
of cofinite subgroups in G satisfying equation (4.1), no telescoping of
![]() $ \mathcal T$
is compatible with the sequence
$ \mathcal T$
is compatible with the sequence
![]() $(\Gamma _n)_{n=1}^\infty $
, that is, for each sequence
$(\Gamma _n)_{n=1}^\infty $
, that is, for each sequence ![]() ,
,

Proof. It is sufficient to use Theorem 5.4 and the following remark.
Let Y be a G-odometer associated with a decreasing sequence
![]() $(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G such that equation (4.1) holds. Let
$(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G such that equation (4.1) holds. Let
![]() $y\in Y$
. Then,
$y\in Y$
. Then,
![]() $y=(g_n\Gamma _n)_{n=1}^\infty $
with
$y=(g_n\Gamma _n)_{n=1}^\infty $
with
![]() $g_ng_{n+1}^{-1}\in \Gamma _n$
for each
$g_ng_{n+1}^{-1}\in \Gamma _n$
for each
![]() $n\in \mathbb N$
. Of course,
$n\in \mathbb N$
. Of course, ![]() and the sequence
and the sequence
![]() $(g_n\Gamma _ng_n^{-1})_{n=1}^\infty $
satisfies equation (4.1). Denote by
$(g_n\Gamma _ng_n^{-1})_{n=1}^\infty $
satisfies equation (4.1). Denote by
![]() $Y_y$
the space of the G-odometer associated with
$Y_y$
the space of the G-odometer associated with
![]() $(g_n\Gamma _ng_n^{-1})_{n=1}^\infty $
. Then there is a canonical G-equivariant homeomorphism
$(g_n\Gamma _ng_n^{-1})_{n=1}^\infty $
. Then there is a canonical G-equivariant homeomorphism
![]() $\varphi _y:Y\to Y_y$
. It is well defined by the formula
$\varphi _y:Y\to Y_y$
. It is well defined by the formula
It follows that there is a G-equivariant map from X to Y if and only if there is a G-equivariant map from X to
![]() $Y_y$
.
$Y_y$
.
In a similar way, we obtain a criterion when a non-singular
![]() $(C,F)$
-action is not isomorphic to any non-singular odometer.
$(C,F)$
-action is not isomorphic to any non-singular odometer.
Corollary 5.7. Let T be the non-singular
![]() $(C,F)$
-action of G associated with a sequence
$(C,F)$
-action of G associated with a sequence
![]() $\mathcal T$
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then T is not isomorphic to any non-singular odometer if and only if for each decreasing sequence
$\mathcal T$
satisfying equations (2.1)–(2.3) and Proposition 2.10(ii). Then T is not isomorphic to any non-singular odometer if and only if for each decreasing sequence ![]() of cofinite subgroups in G satisfying equation (4.1) and each increasing sequence
of cofinite subgroups in G satisfying equation (4.1) and each increasing sequence
![]() $\boldsymbol q$
of non-negative integers such that the
$\boldsymbol q$
of non-negative integers such that the
![]() $\boldsymbol q$
-telescoping
$\boldsymbol q$
-telescoping
![]() $\widetilde {\mathcal T}$
of
$\widetilde {\mathcal T}$
of
![]() $\mathcal T$
is compatible with the point
$\mathcal T$
is compatible with the point
![]() $(\Gamma _n)_{n=1}^\infty \in \projlim _{n\to \infty }G/\Gamma _n$
, there exist
$(\Gamma _n)_{n=1}^\infty \in \projlim _{n\to \infty }G/\Gamma _n$
, there exist
![]() $n>0$
and
$n>0$
and
![]() $\epsilon _0>0$
such that for each
$\epsilon _0>0$
such that for each
![]() $l>0$
,
$l>0$
,
![]() $D_l\subset G/\Gamma _l$
and
$D_l\subset G/\Gamma _l$
and
![]() $M>n$
, there is
$M>n$
, there is
![]() $m>M$
with
$m>M$
with
We state one more corollary from Theorems 5.4 and 2.19 on the existence of minimal Radon uniquely ergodic topological models for rank-one non-singular extensions of non-singular odometers.
Corollary 5.8. Let
![]() $(X,\mu ,T)$
be a rank-one non-singular action of G. Let T have a non-singular odometer factor
$(X,\mu ,T)$
be a rank-one non-singular action of G. Let T have a non-singular odometer factor
![]() $(Y,\nu , O)$
and let
$(Y,\nu , O)$
and let
![]() $\pi :X\to Y$
stand for the corresponding G-equivariant factor mapping with
$\pi :X\to Y$
stand for the corresponding G-equivariant factor mapping with
![]() $\nu =\mu \circ \pi ^{-1}$
. Then there exist a locally compact Cantor space
$\nu =\mu \circ \pi ^{-1}$
. Then there exist a locally compact Cantor space
![]() $\widetilde X$
, a minimal Radon uniquely ergodic free continuous action
$\widetilde X$
, a minimal Radon uniquely ergodic free continuous action
![]() $\widetilde T$
of G on
$\widetilde T$
of G on
![]() $\widetilde X$
, a continuous G-equivariant mapping
$\widetilde X$
, a continuous G-equivariant mapping
![]() $\widetilde \pi :\widetilde X\to Y$
and a Borel isomorphism
$\widetilde \pi :\widetilde X\to Y$
and a Borel isomorphism
![]() $R:X\to \widetilde X$
such that:
$R:X\to \widetilde X$
such that:
-
•
 $\widetilde \mu :=\mu \circ R^{-1}$
is a Radon measure on
$\widetilde \mu :=\mu \circ R^{-1}$
is a Radon measure on
 $\widetilde X$
;
$\widetilde X$
; -
•
 $RT_g=\widetilde T_gR$
for each
$RT_g=\widetilde T_gR$
for each
 $g\in G$
;
$g\in G$
; -
• the function
 ${d\widetilde \mu \circ \widetilde T_g}/{d\widetilde \mu }:\widetilde X\to \mathbb R^*$
is continuous for each
${d\widetilde \mu \circ \widetilde T_g}/{d\widetilde \mu }:\widetilde X\to \mathbb R^*$
is continuous for each
 $g\in G$
;
$g\in G$
; -
•
 $\widetilde T$
is Radon
$\widetilde T$
is Radon
 $({d\widetilde \mu \circ \widetilde T_g}/{d\widetilde \mu })_{g\in G}$
-uniquely ergodic; and
$({d\widetilde \mu \circ \widetilde T_g}/{d\widetilde \mu })_{g\in G}$
-uniquely ergodic; and -
•
 $\widetilde \pi R=\pi $
.
$\widetilde \pi R=\pi $
.
We can also characterize the class of quasi-invariant measures for odometers that appear as factors of rank-one actions. Let
![]() $(Y,O)$
be the topological G-odometer associated with a decreasing sequence
$(Y,O)$
be the topological G-odometer associated with a decreasing sequence
![]() $(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups
$(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups
![]() $\Gamma _n$
of G satisfying equation (4.1). Let a sequence
$\Gamma _n$
of G satisfying equation (4.1). Let a sequence
![]() $\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equation (2.1)–(2.4) and
$\mathcal T=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfy equation (2.1)–(2.4) and
![]() $C_n\subset \Gamma _n$
for each
$C_n\subset \Gamma _n$
for each
![]() $n>0$
. Denote by
$n>0$
. Denote by
![]() $\mu _{\mathcal F}$
the
$\mu _{\mathcal F}$
the
![]() $(C,F)$
-measure determined by the sequence
$(C,F)$
-measure determined by the sequence
![]() $(\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Let X stand for the space of
$(\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Let X stand for the space of
![]() $\mu _{\mathcal {F}}$
. We define a mapping
$\mu _{\mathcal {F}}$
. We define a mapping
![]() $\pi _{\mathcal F}:X\to Y$
by setting
$\pi _{\mathcal F}:X\to Y$
by setting
if
![]() $x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n\subset X$
for some
$x=(f_n,c_{n+1},c_{n+2},\ldots )\in X_n\subset X$
for some
![]() $n\ge 0$
. Then
$n\ge 0$
. Then
![]() $\pi _{\mathcal F}$
is well defined and continuous. Let
$\pi _{\mathcal F}$
is well defined and continuous. Let
We deduce the following claim from Corollary 5.8.
Corollary 5.9. Each measure
![]() $\nu \in \mathcal M_{Y}$
is quasi-invariant under O. A Borel measure
$\nu \in \mathcal M_{Y}$
is quasi-invariant under O. A Borel measure
![]() $\nu $
on Y is equivalent to a measure belonging to
$\nu $
on Y is equivalent to a measure belonging to
![]() $\mathcal M_{Y}$
if and only if there is a rank-one non-singular G-action T such that
$\mathcal M_{Y}$
if and only if there is a rank-one non-singular G-action T such that
![]() $(Y,O,\nu )$
is a measurable factor of T.
$(Y,O,\nu )$
is a measurable factor of T.
6. Examples
6.1. Non-odometer rank-one
 ${\mathbb Z}$
-action with odometer factor
${\mathbb Z}$
-action with odometer factor
In [Reference Foreman, Gao, Hill, Silva and WeissFo–We], an example of classical rank-one finite measure preserving
![]() ${\mathbb Z}$
-action T is constructed such that:
${\mathbb Z}$
-action T is constructed such that:
-
• T has the 2-adic odometer as a factor; but
-
• T is not isomorphic to any odometer.
We remind that given a prime p, the p-adic odometer is associated with the sequence
of cofinite subgroups in
![]() ${\mathbb Z}$
. The argument in [Reference Foreman, Gao, Hill, Silva and WeissFo–We] is based on their description of the odometer factors of rank-one transformations (that result is generalized in our Theorem 5.4). We now consider their example from another point of view, bypassing the use of any version of Theorem 5.4. Our approach is more direct and leads to stronger results.
${\mathbb Z}$
. The argument in [Reference Foreman, Gao, Hill, Silva and WeissFo–We] is based on their description of the odometer factors of rank-one transformations (that result is generalized in our Theorem 5.4). We now consider their example from another point of view, bypassing the use of any version of Theorem 5.4. Our approach is more direct and leads to stronger results.
Example 6.1. Let
![]() $G={\mathbb Z}$
. We construct a measure preserving (classical) rank-one
$G={\mathbb Z}$
. We construct a measure preserving (classical) rank-one
![]() ${\mathbb Z}$
-action T on a probability space
${\mathbb Z}$
-action T on a probability space
![]() $(X,\mu )$
such that:
$(X,\mu )$
such that:
-
•
 $(X,\mu ,T)$
has a proper 2-adic odometer factor
$(X,\mu ,T)$
has a proper 2-adic odometer factor
 $(Y,\nu ,O)$
;
$(Y,\nu ,O)$
; -
•
 $(Y,\nu ,O)$
is the Kronecker factor of
$(Y,\nu ,O)$
is the Kronecker factor of
 $(X,\mu ,T)$
, that is, O is the maximal factor of T with a pure discrete spectrum;
$(X,\mu ,T)$
, that is, O is the maximal factor of T with a pure discrete spectrum; -
• the projection
 $(X,\mu )\to (Y,\nu )$
is uncountable-to-one (mod 0), that is, the corresponding conditional measures on fibres are non-atomic.
$(X,\mu )\to (Y,\nu )$
is uncountable-to-one (mod 0), that is, the corresponding conditional measures on fibres are non-atomic.
We set
![]() $h_0:=0$
and
$h_0:=0$
and
![]() $h_{n+1}:=4h_n+2^{n+1}$
for each
$h_{n+1}:=4h_n+2^{n+1}$
for each
![]() $n\in \mathbb N$
. It follows that
$n\in \mathbb N$
. It follows that
![]() $h_n=2^n(2^{n+1}-1)$
for each
$h_n=2^n(2^{n+1}-1)$
for each
![]() $n\ge 0$
. We let
$n\ge 0$
. We let
 $$ \begin{align*} \begin{aligned} F_n:=\{0,\ldots,h_n-1\}, \quad C_{n+1}:=\{0,h_n,2h_n+2^{n+1},3h_n+2^{n+1}\},\\ \nu_n(f)=\frac 1{4^n}\quad \text{for each } f\in F_n\quad\text{and}\quad \kappa_n(c)=\frac 14\quad \text{for each } c\in C_{n+1} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} F_n:=\{0,\ldots,h_n-1\}, \quad C_{n+1}:=\{0,h_n,2h_n+2^{n+1},3h_n+2^{n+1}\},\\ \nu_n(f)=\frac 1{4^n}\quad \text{for each } f\in F_n\quad\text{and}\quad \kappa_n(c)=\frac 14\quad \text{for each } c\in C_{n+1} \end{aligned} \end{align*} $$
for every
![]() $n\ge 0$
. Then the sequence
$n\ge 0$
. Then the sequence
![]() $\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
$\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
satisfies equations (2.1)–(2.3) and Proposition 2.10(ii). Denote by
![]() $(X,\mu , T)$
the
$(X,\mu , T)$
the
![]() $(C,F)$
-action of
$(C,F)$
-action of
![]() ${\mathbb Z}$
associated with
${\mathbb Z}$
associated with
![]() $\mathcal T$
. Then T is of classical rank one along
$\mathcal T$
. Then T is of classical rank one along
![]() $(F_n)_{n=0}^\infty $
. We note that T is the transformation that was studied in [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. Of course, T preserves
$(F_n)_{n=0}^\infty $
. We note that T is the transformation that was studied in [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. Of course, T preserves
![]() $\mu $
and
$\mu $
and
![]() $\mu (X)<\infty $
. We have that
$\mu (X)<\infty $
. We have that
 $$ \begin{align*} \mu(X)=\mu(X_0)+\sum_{n=1}^\infty 2^n\mu([0]_n)=1+\sum_{n=1}^\infty \frac{2^n}{4^n}=2. \end{align*} $$
$$ \begin{align*} \mu(X)=\mu(X_0)+\sum_{n=1}^\infty 2^n\mu([0]_n)=1+\sum_{n=1}^\infty \frac{2^n}{4^n}=2. \end{align*} $$
Denote by
![]() $(Y, O)$
the 2-adic
$(Y, O)$
the 2-adic
![]() ${\mathbb Z}$
-odometer. Then the transformation
${\mathbb Z}$
-odometer. Then the transformation
![]() $O_1$
acts on the compact metric group
$O_1$
acts on the compact metric group
![]() $Y:=\projlim _{n\to \infty } {\mathbb Z}/2^n{\mathbb Z}$
by translation with the element
$Y:=\projlim _{n\to \infty } {\mathbb Z}/2^n{\mathbb Z}$
by translation with the element
![]() $(1+2{\mathbb Z}, 1+2^2{\mathbb Z}, 1+2^3{\mathbb Z},\ldots )\in Y$
. Let
$(1+2{\mathbb Z}, 1+2^2{\mathbb Z}, 1+2^3{\mathbb Z},\ldots )\in Y$
. Let
![]() $\nu $
stand for the Haar measure on Y. Since each element of
$\nu $
stand for the Haar measure on Y. Since each element of
![]() $C_n$
is divisible by
$C_n$
is divisible by
![]() $2^{n-1}$
for every
$2^{n-1}$
for every
![]() $n>0$
, it follows that O is a factor of T. The corresponding
$n>0$
, it follows that O is a factor of T. The corresponding
![]() $(\mathcal T, 0)$
-factor mapping
$(\mathcal T, 0)$
-factor mapping
![]() $\pi :X\to Y$
is well defined by the formula:
$\pi :X\to Y$
is well defined by the formula:
if ![]() for some
for some
![]() $n\ge 0$
(see Definition 3.2). Since the measure
$n\ge 0$
(see Definition 3.2). Since the measure
![]() $\mu \circ \pi ^{-1}$
is invariant under O, it follows that
$\mu \circ \pi ^{-1}$
is invariant under O, it follows that
![]() $\mu \circ \pi ^{-1}$
is proportional to
$\mu \circ \pi ^{-1}$
is proportional to
![]() $\nu $
. More precisely,
$\nu $
. More precisely, ![]() .
.
We now show that if
![]() $\unicode{x3bb} $
is an eigenvalue of T, then there is
$\unicode{x3bb} $
is an eigenvalue of T, then there is
![]() $n>0$
such that
$n>0$
such that
![]() $\unicode{x3bb} ^{2^n}=1$
. Since
$\unicode{x3bb} ^{2^n}=1$
. Since
![]() $\# C_m=4$
for each m, it follows from [Reference Danilenko and VieprikDaVi, Corollary 3.8] that
$\# C_m=4$
for each m, it follows from [Reference Danilenko and VieprikDaVi, Corollary 3.8] that
As
![]() $ 4^{m}=2h_{m-1}+2^m\in C_m, $
we obtain that
$ 4^{m}=2h_{m-1}+2^m\in C_m, $
we obtain that
![]() $\lim _{m\to \infty }\unicode{x3bb} ^{4^m}=1$
. This is only possible if
$\lim _{m\to \infty }\unicode{x3bb} ^{4^m}=1$
. This is only possible if
![]() $\unicode{x3bb} $
is a dyadic root of
$\unicode{x3bb} $
is a dyadic root of
![]() $1$
, as desired. (Indeed, observe that
$1$
, as desired. (Indeed, observe that
![]() $\unicode{x3bb} ^{4^{m+1}}=(\unicode{x3bb} ^{4^m})^4$
and iterate.) However, denote by
$\unicode{x3bb} ^{4^{m+1}}=(\unicode{x3bb} ^{4^m})^4$
and iterate.) However, denote by ![]() the
the
![]() $\sigma $
-algebra of all measurable subsets in Y. Let
$\sigma $
-algebra of all measurable subsets in Y. Let ![]() . Then each eigenfunction of T whose eigenvalue is a 2-adic root of
. Then each eigenfunction of T whose eigenvalue is a 2-adic root of
![]() $1$
is
$1$
is ![]() -measurable. It follows that the
-measurable. It follows that the ![]() is the Kronecker factor of T.
is the Kronecker factor of T.
We now show that the Kronecker factor is proper, that is, that the spectrum of T has a continuous component. Moreover, we prove that the extension
![]() ${T\to O}$
is uncountable-to-one. For each
${T\to O}$
is uncountable-to-one. For each
![]() $n>0$
, we let
$n>0$
, we let
![]() $C_n^{(1)}:=\{0,h_{n-1}\}$
and
$C_n^{(1)}:=\{0,h_{n-1}\}$
and
![]() $C_n^{(2)}:=\{0,2h_{n-1}+2^n\}=\{0,4^n\}.$
Then,
$C_n^{(2)}:=\{0,2h_{n-1}+2^n\}=\{0,4^n\}.$
Then,
![]() $C_n=C_n^{(1)}+C_n^{(2)}$
. For
$C_n=C_n^{(1)}+C_n^{(2)}$
. For
![]() $j=1,2$
, let
$j=1,2$
, let ![]() . Then,
. Then,
![]() $X_0^{(j)}$
is a compact subset of
$X_0^{(j)}$
is a compact subset of
![]() $X_0$
. Given
$X_0$
. Given
![]() $x=(c_1,c_2,\ldots )\in X_0^{(1)}$
and
$x=(c_1,c_2,\ldots )\in X_0^{(1)}$
and
![]() $z=(d_1,d_2,\ldots )\in X_0^{(2)}$
, the sum
$z=(d_1,d_2,\ldots )\in X_0^{(2)}$
, the sum
is well defined. (Note that
![]() $X_0^{(1)}$
,
$X_0^{(1)}$
,
![]() $X_0^{(2)}$
and
$X_0^{(2)}$
and
![]() $X_0$
are compact subsets of the Polish Abelian group
$X_0$
are compact subsets of the Polish Abelian group
![]() ${\mathbb Z}^{\mathbb {N}}$
.) Moreover, the mapping
${\mathbb Z}^{\mathbb {N}}$
.) Moreover, the mapping
![]() $ (x,z)\mapsto x+z $
is a homeomorphism of the Cartesian product
$ (x,z)\mapsto x+z $
is a homeomorphism of the Cartesian product
![]() $X_0^{(1)}\times X_0^{(2)}$
onto
$X_0^{(1)}\times X_0^{(2)}$
onto
![]() $X_0$
and
$X_0$
and
Endow
![]() $X_0^{(1)}$
and
$X_0^{(1)}$
and
![]() $X_0^{(2)}$
with the infinite products
$X_0^{(2)}$
with the infinite products
![]() $\mu ^{(1)}$
and
$\mu ^{(1)}$
and
![]() $\mu ^{(2)}$
of the equidistributions on
$\mu ^{(2)}$
of the equidistributions on
![]() $C_n^{(1)}$
and
$C_n^{(1)}$
and
![]() $C_n^{(2)}$
, respectively,
$C_n^{(2)}$
, respectively,
![]() $n\in \mathbb N$
. We claim that the restriction of
$n\in \mathbb N$
. We claim that the restriction of
![]() $\pi $
to
$\pi $
to
![]() $X_0^{(j)}$
is one-to-one for
$X_0^{(j)}$
is one-to-one for
![]() $j=1,2$
. It is straightforward to verify that for each
$j=1,2$
. It is straightforward to verify that for each
![]() $x=(c_m)_{m=1}^\infty \in X_0$
,
$x=(c_m)_{m=1}^\infty \in X_0$
,
 $$ \begin{align} \pi(x)=\bigg(\bigg(\sum_{m=1}^nc_m^1+\sum_{1\le m< n/2}c_m^2\bigg)+2^n{\mathbb Z}\bigg)_{n=1}^\infty\in Y, \end{align} $$
$$ \begin{align} \pi(x)=\bigg(\bigg(\sum_{m=1}^nc_m^1+\sum_{1\le m< n/2}c_m^2\bigg)+2^n{\mathbb Z}\bigg)_{n=1}^\infty\in Y, \end{align} $$
where
![]() $c_m^j\in C_m^{(j)}$
and
$c_m^j\in C_m^{(j)}$
and
![]() $c_m=c_m^1+c_m^2$
for each m. Take two points
$c_m=c_m^1+c_m^2$
for each m. Take two points
![]() $x=(c_1^1,c_2^1,\ldots )\in X_0^{(1)}$
and
$x=(c_1^1,c_2^1,\ldots )\in X_0^{(1)}$
and
![]() $y=(d_1^1,d_2^1,\ldots )\in X_0^{(1)}$
such that
$y=(d_1^1,d_2^1,\ldots )\in X_0^{(1)}$
such that
![]() $\pi (x)=\pi (y)$
. It follows from equation (6.2) that
$\pi (x)=\pi (y)$
. It follows from equation (6.2) that
![]() $c_1^1=d_1^1\pmod 2$
,
$c_1^1=d_1^1\pmod 2$
,
![]() $c_1^1+c_2^1=d_1^1+d_2^1\pmod {2^2}$
, …. The first equality implies that
$c_1^1+c_2^1=d_1^1+d_2^1\pmod {2^2}$
, …. The first equality implies that
![]() $d_1^1=c_1^1$
. Therefore, the second equality is equivalent to
$d_1^1=c_1^1$
. Therefore, the second equality is equivalent to
![]() $c_2^1=d_2^1\pmod {2^2}$
, which, in turn, yields that
$c_2^1=d_2^1\pmod {2^2}$
, which, in turn, yields that
![]() $d_2^1=c_2^1$
. By the induction,
$d_2^1=c_2^1$
. By the induction,
![]() $d^1_n=c^1_n$
for each
$d^1_n=c^1_n$
for each
![]() $n>0$
, that is,
$n>0$
, that is,
![]() $x=y$
, as desired. It now follows that the mapping
$x=y$
, as desired. It now follows that the mapping

is bijective for each
![]() $n>0$
. Hence,
$n>0$
. Hence,
![]() $\pi $
maps
$\pi $
maps
![]() $X_0^{(1)}$
bijectively (and homeomorphically) onto Y. Moreover,
$X_0^{(1)}$
bijectively (and homeomorphically) onto Y. Moreover,
![]() $\pi $
maps
$\pi $
maps
![]() $\mu ^{(1)}$
to
$\mu ^{(1)}$
to
![]() $\nu $
. In a similar way, one can check that
$\nu $
. In a similar way, one can check that
![]() $\pi $
maps
$\pi $
maps
![]() $X_0^{(2)}$
bijectively (and homeomorphically) onto the closed subset
$X_0^{(2)}$
bijectively (and homeomorphically) onto the closed subset
![]() $\pi (X_0^{(2)})\subset Y$
. Given
$\pi (X_0^{(2)})\subset Y$
. Given
![]() $y\in Y$
and
$y\in Y$
and
![]() $z\in X_0^{(2)}$
, we define an element
$z\in X_0^{(2)}$
, we define an element
![]() $Q(y,z)\in X_0^{(1)}$
by the formula
$Q(y,z)\in X_0^{(1)}$
by the formula
Of course,
![]() $Q(y,z)$
is well defined. Moreover, the mapping
$Q(y,z)$
is well defined. Moreover, the mapping
is continuous. If we fix
![]() $y\in Y$
, then the mapping
$y\in Y$
, then the mapping
![]() $ X_0^{(2)}\ni z\mapsto Q(y,z)\in X_0^{(1)}$
is one-to-one. Of course, for each
$ X_0^{(2)}\ni z\mapsto Q(y,z)\in X_0^{(1)}$
is one-to-one. Of course, for each
![]() $y\in Y$
,
$y\in Y$
,
Hence,
![]() $\pi ^{-1}(y)$
is uncountable. Moreover, the corresponding conditional measure on the fibre
$\pi ^{-1}(y)$
is uncountable. Moreover, the corresponding conditional measure on the fibre
![]() $X_0\cap \pi ^{-1}(y)$
is the image of
$X_0\cap \pi ^{-1}(y)$
is the image of
![]() $\mu ^{(2)}$
under the mapping
$\mu ^{(2)}$
under the mapping
Hence, the conditional measure on
![]() $X_0\cap \pi ^{-1}(y)$
is non-atomic for each
$X_0\cap \pi ^{-1}(y)$
is non-atomic for each
![]() $y\in Y$
. In particular,
$y\in Y$
. In particular,
![]() $\pi $
is uncountable-to-one.
$\pi $
is uncountable-to-one.
Remark 6.2.
-
(i) The existence of the 2-adic odometer factor O of T in Example 6.1 was proved in [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. It was shown there that O is maximal in the family of odometer factors of T. We refine this result by showing in Example 6.1 that O is the Kronecker factor of T. The claims that T is an uncountable-to-one extension of O and that T has a continuous part in the spectrum are new.
-
(ii) Perhaps the simplest example of non-odometer rank-one
 ${\mathbb Z}$
-action with the maximal odometer factor
${\mathbb Z}$
-action with the maximal odometer factor
 $O=(O_n)_{n\in {\mathbb Z}}$
is the following one. Let R be an irrational rotation on the circle. Then the transformation
$O=(O_n)_{n\in {\mathbb Z}}$
is the following one. Let R be an irrational rotation on the circle. Then the transformation
 $S := O_1 \times R$
is an ergodic transformation with pure discrete spectrum. Hence, it is of rank one [Reference del JuncodJ1]. Of course,
$S := O_1 \times R$
is an ergodic transformation with pure discrete spectrum. Hence, it is of rank one [Reference del JuncodJ1]. Of course,
 $O_1$
is the maximal odometer factor of S. Of course, S is not isomorphic to any odometer (as the discrete spectrum of S has elements of infinite order). Obviously, S is rigid. However, in contrast with T from Example 6.1, the spectrum of S is purely discrete.
$O_1$
is the maximal odometer factor of S. Of course, S is not isomorphic to any odometer (as the discrete spectrum of S has elements of infinite order). Obviously, S is rigid. However, in contrast with T from Example 6.1, the spectrum of S is purely discrete.
6.2. Non-singular counterparts of Example 6.1
We first recall briefly the concepts of the associated flow of an ergodic equivalence relation, Krieger’s type and AT-flow. For details, we refer to the survey [Reference Danilenko, Silva and MeyersDaSi] and references therein. Let
![]() $\mathcal R$
be a countable Borel equivalence relation on a standard
$\mathcal R$
be a countable Borel equivalence relation on a standard
![]() $\sigma $
-finite measure space
$\sigma $
-finite measure space
![]() $(Z,\gamma )$
. Assume that
$(Z,\gamma )$
. Assume that
![]() $\mathcal R$
is
$\mathcal R$
is
![]() $\gamma $
-non-singular and ergodic. This means that if a Borel subset
$\gamma $
-non-singular and ergodic. This means that if a Borel subset
![]() $A\subset Z$
is
$A\subset Z$
is
![]() $\gamma $
-null, then the
$\gamma $
-null, then the
![]() $\mathcal R$
-saturation of A is also
$\mathcal R$
-saturation of A is also
![]() $\gamma $
-null, and each
$\gamma $
-null, and each
![]() $\mathcal R$
-invariant (that is,
$\mathcal R$
-invariant (that is,
![]() $\mathcal R$
-saturated) Borel subset of Z is either
$\mathcal R$
-saturated) Borel subset of Z is either
![]() $\gamma $
-null or
$\gamma $
-null or
![]() $\gamma $
-conull. Denote by
$\gamma $
-conull. Denote by
![]() $\rho _\gamma :\mathcal R\to \mathbb R^*_+$
the Radon–Nikodym cocycle of
$\rho _\gamma :\mathcal R\to \mathbb R^*_+$
the Radon–Nikodym cocycle of
![]() $\mathcal R$
. Endow the product space
$\mathcal R$
. Endow the product space
![]() $Z\times \mathbb R$
with the product measure
$Z\times \mathbb R$
with the product measure
![]() $\gamma \otimes \text {Leb}$
. We define an equivalence relation
$\gamma \otimes \text {Leb}$
. We define an equivalence relation
![]() $\mathcal R(\log \rho _\gamma )$
on
$\mathcal R(\log \rho _\gamma )$
on
![]() $Z\times \mathbb R$
by setting
$Z\times \mathbb R$
by setting
Then,
![]() $\mathcal R(\log \rho _\gamma )$
is countable,
$\mathcal R(\log \rho _\gamma )$
is countable,
![]() $(\mu \otimes \text {Leb})$
-non-singular but not necessarily ergodic. Denote by
$(\mu \otimes \text {Leb})$
-non-singular but not necessarily ergodic. Denote by ![]() the
the
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal R(\log \rho _\gamma )$
-invariant subsets. Let
$\mathcal R(\log \rho _\gamma )$
-invariant subsets. Let
![]() $V=(V_s)_{s\in \mathbb R}$
denote the action of
$V=(V_s)_{s\in \mathbb R}$
denote the action of
![]() $\mathbb R$
on
$\mathbb R$
on
![]() $Z\times \mathbb R$
by translations along the second coordinate, that is,
$Z\times \mathbb R$
by translations along the second coordinate, that is,
![]() $V_s(z,t)=(z,t+s)$
. Of course,
$V_s(z,t)=(z,t+s)$
. Of course, ![]() is invariant under V. The dynamical system
is invariant under V. The dynamical system ![]() is called the flow associated with
is called the flow associated with
![]() $\mathcal R$
. The associated flow is non-singular and ergodic. We denote it by
$\mathcal R$
. The associated flow is non-singular and ergodic. We denote it by
![]() $W^{\mathcal {R}}$
. We will need the following two well-known properties of the associated flows.
$W^{\mathcal {R}}$
. We will need the following two well-known properties of the associated flows.
-
(*) If
 $A\subset Z$
is of positive measure
$A\subset Z$
is of positive measure
 $\gamma $
, then the associated flow of
$\gamma $
, then the associated flow of
 $\mathcal R\restriction A$
is isomorphic to the associated flow of
$\mathcal R\restriction A$
is isomorphic to the associated flow of
 $\mathcal R$
.
$\mathcal R$
. -
(**) If
 $(Z,\gamma )=(Z_1,\gamma _1)\otimes (Z_2,\gamma _2)$
,
$(Z,\gamma )=(Z_1,\gamma _1)\otimes (Z_2,\gamma _2)$
,
 $\mathcal R=\mathcal R_1\otimes \mathcal R_2$
and
$\mathcal R=\mathcal R_1\otimes \mathcal R_2$
and
 $W^{\mathcal R_1}$
is free and transitive, then
$W^{\mathcal R_1}$
is free and transitive, then
 $W^{\mathcal R}$
is isomorphic to
$W^{\mathcal R}$
is isomorphic to
 $W^{\mathcal R_2}$
.
$W^{\mathcal R_2}$
.
An ergodic non-singular flow V is called an AT-flow if there is a sequence
![]() $(A_n,\alpha _n)_{n=1}^\infty $
of finite subsets
$(A_n,\alpha _n)_{n=1}^\infty $
of finite subsets
![]() $A_n$
and non-degenerated probability measures
$A_n$
and non-degenerated probability measures
![]() $\alpha _n$
on
$\alpha _n$
on
![]() $A_n$
such that the infinite product measure
$A_n$
such that the infinite product measure
![]() $\bigotimes _{n=1}^\infty \alpha _n$
is non-atomic and V is isomorphic to the associated flow of the tail equivalence relation on the probability space
$\bigotimes _{n=1}^\infty \alpha _n$
is non-atomic and V is isomorphic to the associated flow of the tail equivalence relation on the probability space
![]() $\bigotimes _{n=1}^\infty (A_n,\alpha _n)$
. If, moreover,
$\bigotimes _{n=1}^\infty (A_n,\alpha _n)$
. If, moreover,
![]() $\# A_n=2$
for each n, then we call the corresponding AT-flow finitary. (The class of finitary AT-flows coincides with the class of flows of weights for the ITPFI
$\# A_n=2$
for each n, then we call the corresponding AT-flow finitary. (The class of finitary AT-flows coincides with the class of flows of weights for the ITPFI
![]() $_2$
factors (in the sense of the theory of von Neumann algebras).) For instance, every ergodic flow with pure point spectrum is a finitary AT-flow [Reference Berendschot and VaesBeVa]. If S is an ergodic non-singular G-action on a standard
$_2$
factors (in the sense of the theory of von Neumann algebras).) For instance, every ergodic flow with pure point spectrum is a finitary AT-flow [Reference Berendschot and VaesBeVa]. If S is an ergodic non-singular G-action on a standard
![]() $\sigma $
-finite measure space, then the associated flow of the S-orbit equivalence relation is called the associated flow of S. If the associated flow of S is transitive and aperiodic, then S is called of Krieger type II. If the associated flow of S is transitive and periodic with the least positive period
$\sigma $
-finite measure space, then the associated flow of the S-orbit equivalence relation is called the associated flow of S. If the associated flow of S is transitive and aperiodic, then S is called of Krieger type II. If the associated flow of S is transitive and periodic with the least positive period
![]() $-\log \unicode{x3bb} $
for some
$-\log \unicode{x3bb} $
for some
![]() $\unicode{x3bb} \in (0,1)$
, then S is called of Krieger type III
$\unicode{x3bb} \in (0,1)$
, then S is called of Krieger type III
![]() $_{\unicode{x3bb}} $
. If the associated flow of S is the trivial flow on a singleton, then S is called of Krieger type III
$_{\unicode{x3bb}} $
. If the associated flow of S is the trivial flow on a singleton, then S is called of Krieger type III
![]() $_{1}$
. If S is neither of type II nor of type III
$_{1}$
. If S is neither of type II nor of type III
![]() $_{\unicode{x3bb}} $
for any
$_{\unicode{x3bb}} $
for any
![]() $\unicode{x3bb} \in (0,1]$
, then S is called of Krieger type III
$\unicode{x3bb} \in (0,1]$
, then S is called of Krieger type III
![]() $_{0}$
.
$_{0}$
.
Let
![]() $(X,T)$
,
$(X,T)$
,
![]() $(Y,\nu ,O)$
and
$(Y,\nu ,O)$
and
![]() $\pi :X\to Y$
be the same as in Example 6.1.
$\pi :X\to Y$
be the same as in Example 6.1.
Proposition 6.3. For each finitary AT-flow V, there exists a
![]() $(C,F)$
-measure
$(C,F)$
-measure
![]() $\mu $
on X such that:
$\mu $
on X such that:
-
(i)
 $\mu $
is quasi-invariant under T and hence the non-singular system
$\mu $
is quasi-invariant under T and hence the non-singular system
 $(X,\mu , T)$
is of rank one;
$(X,\mu , T)$
is of rank one; -
(ii) the associated flow of the system
 $(X,\mu ,T)$
is isomorphic to V;
$(X,\mu ,T)$
is isomorphic to V; -
(iii)
 $\mu \circ \pi ^{-1}\sim \nu $
, that is, the 2-adic probability preserving odometer
$\mu \circ \pi ^{-1}\sim \nu $
, that is, the 2-adic probability preserving odometer
 $(Y,\nu ,O)$
is a factor of
$(Y,\nu ,O)$
is a factor of
 $(X,\mu ,T)$
;
$(X,\mu ,T)$
; -
(iv)
 $(Y,\nu ,O)$
is the maximal odometer factor of
$(Y,\nu ,O)$
is the maximal odometer factor of
 $(X,\mu ,T)$
; and
$(X,\mu ,T)$
; and -
(v) the factor mapping
 $\pi $
is uncountable-to-one (mod 0). Hence,
$\pi $
is uncountable-to-one (mod 0). Hence,
 $(X,\mu ,T)$
is not an odometer.
$(X,\mu ,T)$
is not an odometer.
In particular, for each
![]() $\unicode{x3bb} \in [0,1]$
, there is a
$\unicode{x3bb} \in [0,1]$
, there is a
![]() $(C,F)$
-measure
$(C,F)$
-measure
![]() $\mu $
on X such that
$\mu $
on X such that
![]() $(X,\mu ,T)$
is of Krieger type III
$(X,\mu ,T)$
is of Krieger type III
![]() $_{\unicode{x3bb}} $
satisfying properties (i), (iii)–(v).
$_{\unicode{x3bb}} $
satisfying properties (i), (iii)–(v).
Proof. We will use below the notation from §6.1.
Let
![]() $\kappa _n^1$
stand for the equidistribution on
$\kappa _n^1$
stand for the equidistribution on
![]() $C_n^{(1)}$
and let
$C_n^{(1)}$
and let
![]() $\kappa ^1:=\bigotimes _{n=1}^\infty \kappa _n^1$
. As V is finitary AT, there is a sequence
$\kappa ^1:=\bigotimes _{n=1}^\infty \kappa _n^1$
. As V is finitary AT, there is a sequence
![]() $(\kappa _n^{2})_{n=1}^\infty $
of non-degenerated probability measures
$(\kappa _n^{2})_{n=1}^\infty $
of non-degenerated probability measures
![]() $\kappa _n^{2}$
on
$\kappa _n^{2}$
on
![]() $C_n^{(2)}$
such that the infinite product measure
$C_n^{(2)}$
such that the infinite product measure
![]() $\kappa ^2:=\bigotimes _{n=1}^\infty \kappa _n^{2}$
is non-atomic and the associated flow of the tail equivalence relation on
$\kappa ^2:=\bigotimes _{n=1}^\infty \kappa _n^{2}$
is non-atomic and the associated flow of the tail equivalence relation on
![]() $(X_0^{(2)},\kappa ^{2})$
is isomorphic to V. Denote by
$(X_0^{(2)},\kappa ^{2})$
is isomorphic to V. Denote by
![]() $\kappa _n$
the convolution
$\kappa _n$
the convolution
![]() $\kappa _n^1*\kappa _n^2$
. Then,
$\kappa _n^1*\kappa _n^2$
. Then,
![]() $\kappa _n$
is a non-degenerated probability measure on
$\kappa _n$
is a non-degenerated probability measure on
![]() $C_n$
for each
$C_n$
for each
![]() $n\in \mathbb N$
. We now select inductively a sequence
$n\in \mathbb N$
. We now select inductively a sequence
![]() $(\nu _n)_{n=1}^\infty $
of measures on G such that
$(\nu _n)_{n=1}^\infty $
of measures on G such that
![]() $\nu _n$
is supported on
$\nu _n$
is supported on
![]() $F_n$
for each
$F_n$
for each
![]() $n\in \mathbb N$
and equation (2.3) holds. Consider now the sequence
$n\in \mathbb N$
and equation (2.3) holds. Consider now the sequence
![]() $\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Of course, equation (2.2) holds. It is straightforward to verify that Proposition 2.10(iii) holds for
$\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Of course, equation (2.2) holds. It is straightforward to verify that Proposition 2.10(iii) holds for
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $\mu $
denote the
$\mu $
denote the
![]() $(C,F)$
-measure determined by
$(C,F)$
-measure determined by
![]() $(\kappa _n)_{n=1}^\infty $
and
$(\kappa _n)_{n=1}^\infty $
and
![]() $(\nu _{n})_{n=0}^\infty $
. It follows from Proposition 2.10 that
$(\nu _{n})_{n=0}^\infty $
. It follows from Proposition 2.10 that
![]() $\mu $
is quasi-invariant under T. Thus, property (i) holds.
$\mu $
is quasi-invariant under T. Thus, property (i) holds.
According to
![]() $(*)$
, the associated flow of T is isomorphic to the associated flow of the tail equivalence relation on
$(*)$
, the associated flow of T is isomorphic to the associated flow of the tail equivalence relation on
![]() $(X_0,\mu \restriction X_0)$
. Then
$(X_0,\mu \restriction X_0)$
. Then
![]() $(**)$
yields that the later flow is isomorphic to the associated flow of the tail equivalence relation on
$(**)$
yields that the later flow is isomorphic to the associated flow of the tail equivalence relation on
![]() $(X_0^{(2)},\kappa ^{2})$
. Hence, the associated flow of T is isomorphic to V, that is, property (ii) is proven.
$(X_0^{(2)},\kappa ^{2})$
. Hence, the associated flow of T is isomorphic to V, that is, property (ii) is proven.
We deduce from equation (6.1) that
It was shown in §6.1 that
![]() $\kappa ^1\circ \pi ^{-1}=\nu $
. As
$\kappa ^1\circ \pi ^{-1}=\nu $
. As
![]() $\nu $
is the Haar measure on the compact Abelian group Y, we obtain that
$\nu $
is the Haar measure on the compact Abelian group Y, we obtain that
![]() $\nu *(\kappa ^2\circ \pi ^{-1})=\nu $
. Thus,
$\nu *(\kappa ^2\circ \pi ^{-1})=\nu $
. Thus,
![]() $(\mu \restriction X_0)\circ \pi ^{-1}=\nu $
. Hence,
$(\mu \restriction X_0)\circ \pi ^{-1}=\nu $
. Hence,
![]() $\mu \circ \pi ^{-1}\gg \nu $
. As the two measures,
$\mu \circ \pi ^{-1}\gg \nu $
. As the two measures,
![]() $\mu \circ \pi ^{-1}$
and
$\mu \circ \pi ^{-1}$
and
![]() $\nu $
on Y, are quasi-invariant and ergodic under T, it follows that
$\nu $
on Y, are quasi-invariant and ergodic under T, it follows that
![]() $\mu \circ \pi ^{-1}\sim \nu $
. Thus, property (iii) is proven.
$\mu \circ \pi ^{-1}\sim \nu $
. Thus, property (iii) is proven.
If O is not the maximal odometer factor of T, then there is a prime number
![]() $p>2$
such that the homogeneous
$p>2$
such that the homogeneous
![]() ${\mathbb Z}$
-space
${\mathbb Z}$
-space
![]() ${\mathbb Z}/p{\mathbb Z}$
is a factor of T. Since
${\mathbb Z}/p{\mathbb Z}$
is a factor of T. Since
![]() $\# C_n=4$
for each
$\# C_n=4$
for each
![]() $n>0$
, it can be deduced from Theorem 3.3 that each element of
$n>0$
, it can be deduced from Theorem 3.3 that each element of
![]() $C_n$
is divisible by p eventually in n. However,
$C_n$
is divisible by p eventually in n. However,
![]() $4^n\in C_n$
for each n, which is a contradiction. Thus, property (iv) is proven.
$4^n\in C_n$
for each n, which is a contradiction. Thus, property (iv) is proven.
As for property (v), it is proved almost literally in the same way as in Example 6.1.
The second claim of the proposition follows directly from the first one.
6.3. Rank-one
 ${\mathbb Z}^2$
-action without odometer factors but whose generators have
${\mathbb Z}^2$
-action without odometer factors but whose generators have
 ${\mathbb Z}$
-odometer factors
${\mathbb Z}$
-odometer factors
In this section,
![]() $G={\mathbb Z}^2$
. Only finite measure preserving actions of G are considered in this section. In [Reference Johnson and McClendonJoMc, §6], a rank-one
$G={\mathbb Z}^2$
. Only finite measure preserving actions of G are considered in this section. In [Reference Johnson and McClendonJoMc, §6], a rank-one
![]() ${\mathbb Z}^2$
-action T is constructed such that:
${\mathbb Z}^2$
-action T is constructed such that:
-
(a) each of the generators
 $T_{(1,0)}$
and
$T_{(1,0)}$
and
 $T_{(0,1)}$
of T has an odometer factor (as a
$T_{(0,1)}$
of T has an odometer factor (as a
 ${\mathbb Z}$
-action); but
${\mathbb Z}$
-action); but -
(b) T has no
 ${\mathbb Z}^2$
-odometer factors.
${\mathbb Z}^2$
-odometer factors.
The corresponding construction is rather involved (see [Reference Johnson and McClendonJoMc, Theorem 6.1]). We provide a different, elementary example of T possessing properties (a) and (b). To prove that, we do not use any machinery developed in the previous sections.
Example 6.4. Let R be an irrational rotation on the circle
![]() $(\mathbb T,\unicode{x3bb} _{\mathbb {T}})$
and let S be an ergodic rotation on a compact totally disconnected Abelian infinite group Y endowed with the Haar measure
$(\mathbb T,\unicode{x3bb} _{\mathbb {T}})$
and let S be an ergodic rotation on a compact totally disconnected Abelian infinite group Y endowed with the Haar measure
![]() $\unicode{x3bb} _Y$
. Then the dynamical system
$\unicode{x3bb} _Y$
. Then the dynamical system
![]() $O=(S^n)_{n\in {\mathbb Z}}$
is a classical odometer on
$O=(S^n)_{n\in {\mathbb Z}}$
is a classical odometer on
![]() $(Y,\unicode{x3bb} _Y)$
. We now define a
$(Y,\unicode{x3bb} _Y)$
. We now define a
![]() ${\mathbb Z}^2$
-action
${\mathbb Z}^2$
-action
![]() $T=(T_g)_{g\in {\mathbb Z}^2}$
on the product space
$T=(T_g)_{g\in {\mathbb Z}^2}$
on the product space
![]() $(\mathbb T\times Y,\unicode{x3bb} _{\mathbb {T}}\otimes \unicode{x3bb} _Y)$
by setting
$(\mathbb T\times Y,\unicode{x3bb} _{\mathbb {T}}\otimes \unicode{x3bb} _Y)$
by setting
![]() $ T_{(n,m)}:=R^n\times S^m. $
Of course, T is of rank-one along a Følner sequence of rectangles
$ T_{(n,m)}:=R^n\times S^m. $
Of course, T is of rank-one along a Følner sequence of rectangles
![]() $(F_n)_{n=1}^\infty $
in
$(F_n)_{n=1}^\infty $
in
![]() ${\mathbb Z}^2$
. Let
${\mathbb Z}^2$
. Let
![]() $\theta :=(\begin{smallmatrix} 1&0\\ 1& 1 \end{smallmatrix})\in SL_2({\mathbb Z})$
. Then the action
$\theta :=(\begin{smallmatrix} 1&0\\ 1& 1 \end{smallmatrix})\in SL_2({\mathbb Z})$
. Then the action
![]() $\widetilde T:=(T_{\theta (g)})_{g\in {\mathbb Z}^2}$
is of rank-one along the sequence
$\widetilde T:=(T_{\theta (g)})_{g\in {\mathbb Z}^2}$
is of rank-one along the sequence
![]() $(\theta (F_n))_{n=1}^\infty $
. Of course,
$(\theta (F_n))_{n=1}^\infty $
. Of course,
![]() $(\theta (F_n))_{n=1}^\infty $
is also Følner. The generators
$(\theta (F_n))_{n=1}^\infty $
is also Følner. The generators
![]() $\widetilde T_{(1,0)}=R\times S$
and
$\widetilde T_{(1,0)}=R\times S$
and
![]() $\widetilde T_{(0,1)}=I\times S$
of
$\widetilde T_{(0,1)}=I\times S$
of
![]() $\widetilde T$
have S as a factor. Thus, property (a) holds for
$\widetilde T$
have S as a factor. Thus, property (a) holds for
![]() $\widetilde T$
.
$\widetilde T$
.
It remains to show that
![]() $\widetilde T$
satisfies property (b), that is, that
$\widetilde T$
satisfies property (b), that is, that
![]() $\widetilde T$
has no
$\widetilde T$
has no
![]() ${\mathbb Z}^2$
-odometer factors. Suppose that
${\mathbb Z}^2$
-odometer factors. Suppose that
![]() $\widetilde T$
has an odometer factor
$\widetilde T$
has an odometer factor
![]() $\widetilde O$
. Let K be the space of
$\widetilde O$
. Let K be the space of
![]() $\widetilde O$
and let
$\widetilde O$
and let
![]() $\pi :\mathbb T\times Y\to K$
denote the corresponding
$\pi :\mathbb T\times Y\to K$
denote the corresponding
![]() ${\mathbb Z}^2$
-equivariant factor mapping. Then K is a totally disconnected compact Abelian group. Since
${\mathbb Z}^2$
-equivariant factor mapping. Then K is a totally disconnected compact Abelian group. Since
![]() $\widetilde T$
has pure discrete spectrum, there is a compact subgroup
$\widetilde T$
has pure discrete spectrum, there is a compact subgroup
![]() $H\subset \mathbb T\times Y$
such that
$H\subset \mathbb T\times Y$
such that
![]() $K=(\mathbb T\times Y)/H$
and
$K=(\mathbb T\times Y)/H$
and
![]() $\pi (g)=gH$
for each
$\pi (g)=gH$
for each
![]() $g\in \mathbb T\times Y$
. Since
$g\in \mathbb T\times Y$
. Since
![]() $\mathbb T$
is connected and K is totally disconnected, the closed subgroup
$\mathbb T$
is connected and K is totally disconnected, the closed subgroup
![]() $\pi (\mathbb T\times \{0\})\subset K$
is trivial. This means that H contains the subgroup
$\pi (\mathbb T\times \{0\})\subset K$
is trivial. This means that H contains the subgroup
![]() $\mathbb T\times \{0\}$
. Hence, K is a quotient group of
$\mathbb T\times \{0\}$
. Hence, K is a quotient group of
![]() $Y=(\mathbb T\times Y)/(\mathbb T\times \{0\})$
indeed and
$Y=(\mathbb T\times Y)/(\mathbb T\times \{0\})$
indeed and
![]() $\pi $
is the corresponding projection map. It follows that
$\pi $
is the corresponding projection map. It follows that
![]() $\widetilde O$
is not faithful:
$\widetilde O$
is not faithful:
for each
![]() $n\in {\mathbb Z}$
. Since each odometer action is faithful,
$n\in {\mathbb Z}$
. Since each odometer action is faithful,
![]() $\widetilde O$
is not an odometer. Thus, property (b) is proven.
$\widetilde O$
is not an odometer. Thus, property (b) is proven.
According to the terminology of [Reference Johnson and McClendonJoMc] (which is different from ours),
![]() ${\mathbb Z}^2$
-odometers can be non-free. Hence, property (b) can be interpreted as ‘every rank-one factor of T is non-free’.
${\mathbb Z}^2$
-odometers can be non-free. Hence, property (b) can be interpreted as ‘every rank-one factor of T is non-free’.
Remark 6.5. We note that in the example [Reference Johnson and McClendonJoMc, §6], the generators
![]() $T_{(0,1)}$
and
$T_{(0,1)}$
and
![]() $T_{(1,0)}$
are non-ergodic. In Example 6.4,
$T_{(1,0)}$
are non-ergodic. In Example 6.4,
![]() $\widetilde T_{(1,0)}$
is ergodic but
$\widetilde T_{(1,0)}$
is ergodic but
![]() $\widetilde T_{(0,1)}$
is not. However, if we change
$\widetilde T_{(0,1)}$
is not. However, if we change
![]() $\theta $
with the matrix
$\theta $
with the matrix
![]() $\theta ':=(\begin{smallmatrix} 2&1\\1&1\end{smallmatrix})$
, then we obtain a new example of rank-one
$\theta ':=(\begin{smallmatrix} 2&1\\1&1\end{smallmatrix})$
, then we obtain a new example of rank-one
![]() ${\mathbb Z}^2$
-action
${\mathbb Z}^2$
-action
![]() $\widetilde T$
possessing properties (a), (b) and
$\widetilde T$
possessing properties (a), (b) and
-
(c) each of the generators
 $\widetilde T_{(1,0)}$
and
$\widetilde T_{(1,0)}$
and
 $\widetilde T_{(0,1)}$
of
$\widetilde T_{(0,1)}$
of
 $\widetilde T$
is ergodic.
$\widetilde T$
is ergodic.
6.4. Heisenberg group actions of rank one
In this section, we consider the three-dimensional discrete Heisenberg group
![]() $H_3({\mathbb Z})$
. We recall that
$H_3({\mathbb Z})$
. We recall that
 $$ \begin{align*} H_3({\mathbb Z})= \left\{ \begin{pmatrix} 1 & x & z\\ 0&1&y\\ 0&0&1 \end{pmatrix}\Bigg|\, x,y,z\in{\mathbb Z}\right\}. \end{align*} $$
$$ \begin{align*} H_3({\mathbb Z})= \left\{ \begin{pmatrix} 1 & x & z\\ 0&1&y\\ 0&0&1 \end{pmatrix}\Bigg|\, x,y,z\in{\mathbb Z}\right\}. \end{align*} $$
This group is non-Abelian, nilpotent and residually finite. For brevity, we will write
![]() $(x,y,z)$
for the matrix
$(x,y,z)$
for the matrix
![]() $\big(\begin{smallmatrix} 1 & x & z\\ 0&1&y\\ 0&0&1 \end{smallmatrix}\big)$
. It is straightforward to verify that
$\big(\begin{smallmatrix} 1 & x & z\\ 0&1&y\\ 0&0&1 \end{smallmatrix}\big)$
. It is straightforward to verify that

The centre of
![]() $H_3({\mathbb Z})$
is
$H_3({\mathbb Z})$
is
![]() $\{(0,0,z)\mid z\in {\mathbb Z}\}$
. Given
$\{(0,0,z)\mid z\in {\mathbb Z}\}$
. Given
![]() $a,b,c\ge 0$
, we let
$a,b,c\ge 0$
, we let
It is straightforward to verify that if
![]() $a_n\to +\infty $
,
$a_n\to +\infty $
,
![]() $b_n\to +\infty $
,
$b_n\to +\infty $
,
![]() $c_n\to +\infty $
and
$c_n\to +\infty $
and
![]() ${b_n}/{c_n}\to 0$
as
${b_n}/{c_n}\to 0$
as
![]() $n\to \infty $
, then
$n\to \infty $
, then
![]() $(\Pi (a_n,b_n,c_n))_{n=1}^\infty $
is a left Følner sequence in
$(\Pi (a_n,b_n,c_n))_{n=1}^\infty $
is a left Følner sequence in
![]() $H_3({\mathbb Z})$
. If, in addition,
$H_3({\mathbb Z})$
. If, in addition,
![]() ${a_n}/{c_n}\to 0$
, then
${a_n}/{c_n}\to 0$
, then
![]() $(\Pi (a_n,b_n,c_n))_{n=1}^\infty $
is a 2-sided Følner sequence in
$(\Pi (a_n,b_n,c_n))_{n=1}^\infty $
is a 2-sided Følner sequence in
![]() $H_3({\mathbb Z})$
.
$H_3({\mathbb Z})$
.
Example 6.6. We construct a probability preserving
![]() $(C,F)$
-action T of
$(C,F)$
-action T of
![]() $H_3({\mathbb Z})$
that has an odometer factor, but T itself is not isomorphic to any odometer. For that, we first define recurrently a sequence
$H_3({\mathbb Z})$
that has an odometer factor, but T itself is not isomorphic to any odometer. For that, we first define recurrently a sequence
![]() $(h_n)_{n=0}^\infty $
of positive integers by setting
$(h_n)_{n=0}^\infty $
of positive integers by setting
It is easy to check that ![]() for each
for each
![]() $n\ge 0$
. We set
$n\ge 0$
. We set

We now define a sequence
![]() $(C_n,F_{n-1})_{n=1}^\infty $
by setting
$(C_n,F_{n-1})_{n=1}^\infty $
by setting
It is straightforward to check that equation (2.1) is satisfied. We define measures
![]() $\kappa _n$
on
$\kappa _n$
on
![]() $C_n$
and
$C_n$
and
![]() $\nu _n$
on
$\nu _n$
on
![]() $F_n$
by setting
$F_n$
by setting
![]() $\nu _0(1)=1$
and
$\nu _0(1)=1$
and
Let
![]() $\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})$
. Then (2.2) and (2.3) hold for
$\mathcal T:=(C_n,F_{n-1},\kappa _n,\nu _{n-1})$
. Then (2.2) and (2.3) hold for
![]() $\mathcal T$
. Since
$\mathcal T$
. Since ![]() and
and
![]() $\# C_{n+1}=64$
, we obtain that
$\# C_{n+1}=64$
, we obtain that
 $$ \begin{align} \prod_{n>0}\frac{\# F_{n+1}}{\# F_n\#C_{n+1}}=\prod_{n>0}\frac{4^{n+2}-3}{4(4^{n+1}-3)} =\prod_{n>0}\bigg(1+\frac9{4(4^{n+1}-3)}\bigg)<\infty. \end{align} $$
$$ \begin{align} \prod_{n>0}\frac{\# F_{n+1}}{\# F_n\#C_{n+1}}=\prod_{n>0}\frac{4^{n+2}-3}{4(4^{n+1}-3)} =\prod_{n>0}\bigg(1+\frac9{4(4^{n+1}-3)}\bigg)<\infty. \end{align} $$
Of course,
![]() $(F_n)_{n=1}^\infty $
is a 2-sided Følner sequence in
$(F_n)_{n=1}^\infty $
is a 2-sided Følner sequence in
![]() $H_3({\mathbb Z})$
. Hence, Proposition 2.10(ii) holds. Then the
$H_3({\mathbb Z})$
. Hence, Proposition 2.10(ii) holds. Then the
![]() $(C,F)$
-action
$(C,F)$
-action
![]() $T=(T_g)_{g\in H_3({\mathbb Z})}$
associated with
$T=(T_g)_{g\in H_3({\mathbb Z})}$
associated with
![]() $\mathcal T$
is well defined on a measure space
$\mathcal T$
is well defined on a measure space
![]() $(X,\mu )$
, where
$(X,\mu )$
, where
![]() $\mu $
is the
$\mu $
is the
![]() $(C,F)$
-measure determined by
$(C,F)$
-measure determined by
![]() $(\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Moreover, T preserves
$(\kappa _n,\nu _{n-1})_{n=1}^\infty $
. Moreover, T preserves
![]() $\mu $
, that is,
$\mu $
, that is,
![]() $\mu $
is the Haar measure for the
$\mu $
is the Haar measure for the
![]() $(C,F)$
-equivalence relation on X, and
$(C,F)$
-equivalence relation on X, and
![]() $\mu (X)<\infty $
in view of equation (6.3) (see Remark 2.5).
$\mu (X)<\infty $
in view of equation (6.3) (see Remark 2.5).
Next, we define a measure preserving odometer action of
![]() $H_3({\mathbb Z})$
. Given
$H_3({\mathbb Z})$
. Given
![]() $n>0$
, we let
$n>0$
, we let
Then,
![]() $ \Gamma _n$
is a normal cofinite subgroup of
$ \Gamma _n$
is a normal cofinite subgroup of
![]() $H_3({\mathbb Z})$
,
$H_3({\mathbb Z})$
, ![]() and
and
![]() $\bigcap _{n=1}^\infty \Gamma _n=\{1\}$
. Denote by O the
$\bigcap _{n=1}^\infty \Gamma _n=\{1\}$
. Denote by O the
![]() $H_3({\mathbb Z})$
-odometer associated with the sequence
$H_3({\mathbb Z})$
-odometer associated with the sequence
![]() $(\Gamma _n)_{n=1}^\infty $
. We call it the 2-adic odometer action of
$(\Gamma _n)_{n=1}^\infty $
. We call it the 2-adic odometer action of
![]() $H_3({\mathbb Z})$
. This odometer is normal. It is defined on the compact metric group
$H_3({\mathbb Z})$
. This odometer is normal. It is defined on the compact metric group
Denote by
![]() $\nu $
the Haar measure on Y. Since
$\nu $
the Haar measure on Y. Since
![]() $C_{n+1}\subset \Gamma _n$
for each
$C_{n+1}\subset \Gamma _n$
for each
![]() $n\in \mathbb N$
, it follows that
$n\in \mathbb N$
, it follows that
![]() $\mathcal T$
is compatible with
$\mathcal T$
is compatible with
![]() $(\Gamma _n)_{n=1}^\infty \in Y$
. Hence, the
$(\Gamma _n)_{n=1}^\infty \in Y$
. Hence, the
![]() $(\mathcal T, (\Gamma _n)_{n=1}^\infty )$
-factor mapping
$(\mathcal T, (\Gamma _n)_{n=1}^\infty )$
-factor mapping
![]() $\pi _{(\mathcal T,(\Gamma _n)_{n=1}^\infty )}:X\to Y$
intertwines T with O. For brevity, instead of
$\pi _{(\mathcal T,(\Gamma _n)_{n=1}^\infty )}:X\to Y$
intertwines T with O. For brevity, instead of
![]() $\pi _{(\mathcal T,(\Gamma _n)_{n=1}^\infty )}$
, below we will write
$\pi _{(\mathcal T,(\Gamma _n)_{n=1}^\infty )}$
, below we will write
![]() $\pi $
. The measure
$\pi $
. The measure
![]() $\mu \circ \pi ^{-1}$
on Y is finite and invariant under O. Since O is uniquely ergodic, it follows that
$\mu \circ \pi ^{-1}$
on Y is finite and invariant under O. Since O is uniquely ergodic, it follows that ![]() . Thus, the 2-adic
. Thus, the 2-adic
![]() $H_3({\mathbb Z})$
-odometer is a finite measure preserving factor of
$H_3({\mathbb Z})$
-odometer is a finite measure preserving factor of
![]() $(X,\mu , T)$
.
$(X,\mu , T)$
.
We claim that
![]() $(Y,\nu , O)$
is the maximal odometer factor of T, that is, every odometer factor of T is a factor of O. Let
$(Y,\nu , O)$
is the maximal odometer factor of T, that is, every odometer factor of T is a factor of O. Let ![]() be a sequence of cofinite subgroups in
be a sequence of cofinite subgroups in
![]() $H_3({\mathbb Z})$
with
$H_3({\mathbb Z})$
with
![]() $\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Lambda _ng^{-1}=\{1\}$
and let
$\bigcap _{n=1}^\infty \bigcap _{g\in G}g\Lambda _ng^{-1}=\{1\}$
and let
![]() $Q=(Q_g)_{g\in H_3({\mathbb Z})}$
stand for the associated
$Q=(Q_g)_{g\in H_3({\mathbb Z})}$
stand for the associated
![]() $H_3({\mathbb Z})$
-odometer which is defined on the space
$H_3({\mathbb Z})$
-odometer which is defined on the space
![]() $Z:=\projlim _{n\to \infty }H_3({\mathbb Z})/\Lambda _n$
equipped with Haar measure. If there is an
$Z:=\projlim _{n\to \infty }H_3({\mathbb Z})/\Lambda _n$
equipped with Haar measure. If there is an
![]() $H_3({\mathbb Z})$
-equivariant mapping
$H_3({\mathbb Z})$
-equivariant mapping
![]() $\tau :X\to Z$
then, by Theorem 5.4, there exist a sequence
$\tau :X\to Z$
then, by Theorem 5.4, there exist a sequence
![]() $\boldsymbol q=(q_n)_{n=0}^\infty $
and an element
$\boldsymbol q=(q_n)_{n=0}^\infty $
and an element
![]() $z=(g_n\Lambda _n)_{n=1}^\infty \in Z$
such that
$z=(g_n\Lambda _n)_{n=1}^\infty \in Z$
such that ![]() , the
, the
![]() $\boldsymbol q$
-telescoping
$\boldsymbol q$
-telescoping
![]() $\widetilde {\mathcal T}$
of
$\widetilde {\mathcal T}$
of
![]() $\mathcal T$
is compatible with z and
$\mathcal T$
is compatible with z and
![]() $\tau =\pi _{(\widetilde {\mathcal T},z)}\circ \iota _{\boldsymbol q}$
. Replacing
$\tau =\pi _{(\widetilde {\mathcal T},z)}\circ \iota _{\boldsymbol q}$
. Replacing
![]() $\Lambda _n$
with
$\Lambda _n$
with
![]() $g_n^{-1}\Lambda _ng_n$
for each
$g_n^{-1}\Lambda _ng_n$
for each
![]() $n\in \mathbb N$
, we pass to an isomorphic (to Q) odometer as a factor of X (see the proof of Corollary 5.6). We denote it by the same symbol Z. Therefore, without loss of generality, we may assume that
$n\in \mathbb N$
, we pass to an isomorphic (to Q) odometer as a factor of X (see the proof of Corollary 5.6). We denote it by the same symbol Z. Therefore, without loss of generality, we may assume that
![]() $\widetilde {\mathcal T}$
is compatible with
$\widetilde {\mathcal T}$
is compatible with
![]() $z=(\Lambda _n)_{n=1}^\infty $
. It follows that there is
$z=(\Lambda _n)_{n=1}^\infty $
. It follows that there is
![]() $N>0$
such that for each
$N>0$
such that for each
![]() $n>N$
,
$n>N$
,
As
![]() $\# C_{q_n+1}=64$
and
$\# C_{q_n+1}=64$
and ![]() , a version of Fubini’s theorem yields that there exists at least one element
, a version of Fubini’s theorem yields that there exists at least one element ![]() such that
such that
![]() $C_{q_n+1}d\subset \Lambda _n$
. Hence,
$C_{q_n+1}d\subset \Lambda _n$
. Hence,
Therefore, the subgroup
is contained in
![]() $\Lambda _n$
. This implies that
$\Lambda _n$
. This implies that
![]() $\Gamma _{2q_n}\subset \Sigma _n\subset \Lambda _n$
for each
$\Gamma _{2q_n}\subset \Sigma _n\subset \Lambda _n$
for each
![]() $n>0$
. The natural projection
$n>0$
. The natural projection
is
![]() $H_3({\mathbb Z})$
-equivariant for each n. Passing to the projective limit as
$H_3({\mathbb Z})$
-equivariant for each n. Passing to the projective limit as
![]() $n\to \infty $
, we obtain an
$n\to \infty $
, we obtain an
![]() $H_3({\mathbb Z})$
-equivariant projection
$H_3({\mathbb Z})$
-equivariant projection
![]() $\eta :Y\to Z$
. It is straightforward to verify that
$\eta :Y\to Z$
. It is straightforward to verify that
![]() $\tau =\eta \circ \pi $
, as desired.
$\tau =\eta \circ \pi $
, as desired.
It remains to show that
![]() $\pi $
is not one-to-one (mod 0). For that, it suffices to show that the restriction of
$\pi $
is not one-to-one (mod 0). For that, it suffices to show that the restriction of
![]() $\pi $
to
$\pi $
to
![]() $X_0$
is not one-to-one. Let
$X_0$
is not one-to-one. Let
![]() $\kappa _n^1$
and
$\kappa _n^1$
and
![]() $\kappa _n^2$
be the equidistributions on
$\kappa _n^2$
be the equidistributions on
![]() $C^{(1)}_n$
and
$C^{(1)}_n$
and
![]() $C^{(2)}_n$
, respectively,
$C^{(2)}_n$
, respectively,
![]() $n\in \mathbb N$
. We let
$n\in \mathbb N$
. We let

Then,
![]() $X_0, X_0^{(1)}$
and
$X_0, X_0^{(1)}$
and
![]() $X_0^{(2)}$
are compact subsets of the Polish group
$X_0^{(2)}$
are compact subsets of the Polish group
![]() $H_3({\mathbb Z})^{\mathbb {N}}$
. The mapping
$H_3({\mathbb Z})^{\mathbb {N}}$
. The mapping
is a homeomorphism that maps the product measure
![]() $\kappa ^1\otimes \kappa ^2$
to
$\kappa ^1\otimes \kappa ^2$
to
![]() $\mu \restriction X_0$
. Moreover, for each
$\mu \restriction X_0$
. Moreover, for each
![]() $(x^1,x^2)\in X_0^{(1)}\times X_0^{(2)}$
,
$(x^1,x^2)\in X_0^{(1)}\times X_0^{(2)}$
,
Let
![]() $\mathcal Z$
stand for the centre of
$\mathcal Z$
stand for the centre of
![]() $H_3({\mathbb Z})$
. Denote by
$H_3({\mathbb Z})$
. Denote by
![]() $Y_0$
the centre of Y. It is routine to verify that
$Y_0$
the centre of Y. It is routine to verify that
Denote by
![]() $Y_2$
the quotient group
$Y_2$
the quotient group
![]() $Y/Y_0$
and by
$Y/Y_0$
and by
![]() $\omega $
the quotient homomorphism
$\omega $
the quotient homomorphism
![]() $Y\to Y_2$
. Then we obtain a short exact sequence of compact totally disconnected groups
$Y\to Y_2$
. Then we obtain a short exact sequence of compact totally disconnected groups
Denote by
![]() $\unicode{x3bb} _0$
and
$\unicode{x3bb} _0$
and
![]() $\unicode{x3bb} _2$
the Haar measures on
$\unicode{x3bb} _2$
the Haar measures on
![]() $Y_0$
and
$Y_0$
and
![]() $Y_2$
, respectively. It is straightforward to verify that
$Y_2$
, respectively. It is straightforward to verify that
 $$ \begin{align*} Y_2&=\projlim_{n\to\infty}H_3({\mathbb Z})/(\mathcal Z\Gamma_n)=\projlim_{n\to\infty}{\mathbb Z}^2/2^n{\mathbb Z}^2\quad\text{and}\\ &\omega\circ \pi(x^1)= ((a_1,b_1)+2{\mathbb Z}^2,(a_2,b_2)+2^2{\mathbb Z}^2,\ldots) \end{align*} $$
$$ \begin{align*} Y_2&=\projlim_{n\to\infty}H_3({\mathbb Z})/(\mathcal Z\Gamma_n)=\projlim_{n\to\infty}{\mathbb Z}^2/2^n{\mathbb Z}^2\quad\text{and}\\ &\omega\circ \pi(x^1)= ((a_1,b_1)+2{\mathbb Z}^2,(a_2,b_2)+2^2{\mathbb Z}^2,\ldots) \end{align*} $$
for each
![]() $x^1=((a_1,b_1,0),(a_2,b_2,0),\ldots )\in X^{(1)}_0$
. Hence,
$x^1=((a_1,b_1,0),(a_2,b_2,0),\ldots )\in X^{(1)}_0$
. Hence,
![]() $\omega \circ \pi $
is a measure preserving homeomorphism of
$\omega \circ \pi $
is a measure preserving homeomorphism of
![]() $(X_0^{(1)},\kappa ^{1})$
onto
$(X_0^{(1)},\kappa ^{1})$
onto
![]() $(Y_2,\unicode{x3bb} _2)$
. We now define a continuous mapping
$(Y_2,\unicode{x3bb} _2)$
. We now define a continuous mapping
![]() ${s:Y_2\to Y}$
by setting
${s:Y_2\to Y}$
by setting
Then, s is a cross-section of
![]() $\omega $
. Hence, the mapping
$\omega $
. Hence, the mapping
is a well-defined measure preserving homeomorphism of
![]() $(Y,\nu )$
onto the product measure space
$(Y,\nu )$
onto the product measure space
![]() $(Y_0\times Y_2,\unicode{x3bb} _0\otimes \unicode{x3bb} _2)$
. It follows from equations (6.4) and (6.5) that
$(Y_0\times Y_2,\unicode{x3bb} _0\otimes \unicode{x3bb} _2)$
. It follows from equations (6.4) and (6.5) that
for each
![]() $(x^1,x^2)\in X_0^{(1)}\times X_0^{(2)}$
. Moreover,
$(x^1,x^2)\in X_0^{(1)}\times X_0^{(2)}$
. Moreover,
Therefore,
![]() $\pi $
is not one-to-one (
$\pi $
is not one-to-one (
![]() $\mu $
-mod 0) if and only if the mapping
$\mu $
-mod 0) if and only if the mapping
![]() $\pi \restriction X^{(2)}_0\to Y_0$
is not one-to-one (
$\pi \restriction X^{(2)}_0\to Y_0$
is not one-to-one (
![]() $\mu ^{(2)}$
-mod 0).
$\mu ^{(2)}$
-mod 0).
Our purpose now is to show that
![]() $\pi \restriction X^{(2)}_0\to Y_0$
is not one-to-one. Let
$\pi \restriction X^{(2)}_0\to Y_0$
is not one-to-one. Let

![]() ${\kappa }_n^3$
and
${\kappa }_n^3$
and
![]() $\kappa _n^4$
are the equidistributions on
$\kappa _n^4$
are the equidistributions on
![]() $C^{(3)}_{n}$
and
$C^{(3)}_{n}$
and
![]() $C^{(4)}_{n}$
respectively for each
$C^{(4)}_{n}$
respectively for each
![]() $n\ge 0$
, and let
$n\ge 0$
, and let

Then,
![]() $X_0^{(3)}$
and
$X_0^{(3)}$
and
![]() $X_0^{(4)}$
are compact subsets of
$X_0^{(4)}$
are compact subsets of
![]() $H_3({\mathbb Z})^{\mathbb {N}}$
. The mapping
$H_3({\mathbb Z})^{\mathbb {N}}$
. The mapping
is a well-defined homeomorphism that maps the product measure
![]() $\kappa ^3\otimes \kappa ^4$
to
$\kappa ^3\otimes \kappa ^4$
to
![]() $\kappa ^2$
. Moreover, for each
$\kappa ^2$
. Moreover, for each
![]() $(x^3,x^4)\in X_0^{(3)}\times X_0^{(4)}$
,
$(x^3,x^4)\in X_0^{(3)}\times X_0^{(4)}$
,
In view of that, it suffices to show that the mapping
![]() $\pi \restriction X^{(3)}\to Y_0$
is a bijection and
$\pi \restriction X^{(3)}\to Y_0$
is a bijection and
![]() $\kappa ^3\circ (\pi \restriction X^{(3)})^{-1}=\unicode{x3bb} _0$
. We leave a routine verification of these facts to the reader.
$\kappa ^3\circ (\pi \restriction X^{(3)})^{-1}=\unicode{x3bb} _0$
. We leave a routine verification of these facts to the reader.
With the example below, we illustrate that the common concept of normality for odometers is not invariant under isomorphism. The normality depends on the choice of the underlying sequence of
![]() $(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G.
$(\Gamma _n)_{n=1}^\infty $
of cofinite subgroups in G.
Example 6.7. Let
![]() $\Gamma _n:=\{(i2^{n-1},j2^n,k2^n)\in H_3({\mathbb Z})\mid i,j,k\in {\mathbb Z}\}$
. Of course,
$\Gamma _n:=\{(i2^{n-1},j2^n,k2^n)\in H_3({\mathbb Z})\mid i,j,k\in {\mathbb Z}\}$
. Of course,
![]() $\Gamma _n$
is a non-normal cofinite subgroup of
$\Gamma _n$
is a non-normal cofinite subgroup of
![]() $H_3({\mathbb Z})$
and
$H_3({\mathbb Z})$
and ![]() with
with
![]() $\bigcap _{n=1}^\infty \Gamma _n=\{1\}$
. It is easy to see that the largest normal subgroup
$\bigcap _{n=1}^\infty \Gamma _n=\{1\}$
. It is easy to see that the largest normal subgroup
![]() $\widetilde \Gamma _n$
of
$\widetilde \Gamma _n$
of
![]() $\Gamma _n$
is
$\Gamma _n$
is
Thus,
![]() $\widetilde \Gamma _n$
is of index 2 in
$\widetilde \Gamma _n$
is of index 2 in
![]() $\Gamma _n$
for each
$\Gamma _n$
for each
![]() $n>0$
. Denote by
$n>0$
. Denote by
![]() $(Y,O)$
and
$(Y,O)$
and
![]() $(\widetilde Y,\widetilde O)$
the topological odometers associated with
$(\widetilde Y,\widetilde O)$
the topological odometers associated with
![]() $(\Gamma _n)_{n=1}^\infty $
and
$(\Gamma _n)_{n=1}^\infty $
and
![]() $(\widetilde \Gamma _n)_{n=1}^\infty $
, respectively. Then,
$(\widetilde \Gamma _n)_{n=1}^\infty $
, respectively. Then,
![]() $(\widetilde Y,\widetilde O)$
is a normal odometer while
$(\widetilde Y,\widetilde O)$
is a normal odometer while
![]() $(Y,O)$
is not. Moreover,
$(Y,O)$
is not. Moreover,
![]() $(\widetilde Y,\widetilde O)$
is the topological normal cover of
$(\widetilde Y,\widetilde O)$
is the topological normal cover of
![]() $(Y,O)$
. As was shown in §4.2,
$(Y,O)$
. As was shown in §4.2,
![]() $(Y,O)$
is a factor of
$(Y,O)$
is a factor of
![]() $(\widetilde Y,\widetilde O)$
under the natural projection
$(\widetilde Y,\widetilde O)$
under the natural projection
![]() $\omega :\widetilde Y\ni \widetilde y\mapsto \widetilde y H\in \widetilde Y/H=Y$
, where
$\omega :\widetilde Y\ni \widetilde y\mapsto \widetilde y H\in \widetilde Y/H=Y$
, where
is a closed subgroup of
![]() $\widetilde Y$
. Since
$\widetilde Y$
. Since
![]() $\Gamma _{n+1}\subset \widetilde \Gamma _n\subset \Gamma _n$
for each n, it follows that
$\Gamma _{n+1}\subset \widetilde \Gamma _n\subset \Gamma _n$
for each n, it follows that
![]() $\omega $
is one-to-one. Hence,
$\omega $
is one-to-one. Hence,
![]() $\omega $
is an isomorphism of
$\omega $
is an isomorphism of
![]() $\widetilde O$
with O, and
$\widetilde O$
with O, and
![]() $H=\{1\}$
.
$H=\{1\}$
.
7. Comments on the paper [Reference Johnson and McClendonJoMc]
The article [Reference Johnson and McClendonJoMc] by Johnson and McClendon is also devoted to a generalization of [Reference Foreman, Gao, Hill, Silva and WeissFo–We]. However, [Reference Johnson and McClendonJoMc] deals only with probability preserving actions of amenable groups. Moreover, the odometers that appear in their paper are always normal. In this section, we discuss the results from [Reference Johnson and McClendonJoMc] and compare them with ours.
-
(1) ‘Følner rank one’ is rank one according to Definition 2.1. By [Reference Johnson and McClendonJoMc], a measure preserving G-action T on a probability space
 $(X,\mu )$
is called of Følner rank one if Definition 2.1(i) holds and
$(X,\mu )$
is called of Følner rank one if Definition 2.1(i) holds and
 $(F_n)_{n=1}^\infty $
is a Følner sequence in G. We first claim that then, T is free. Indeed, denote by
$(F_n)_{n=1}^\infty $
is a Følner sequence in G. We first claim that then, T is free. Indeed, denote by
 $H_x\subset G$
the stabilizer of T at
$H_x\subset G$
the stabilizer of T at
 $x\in X$
, that is, Let
$x\in X$
, that is, Let $$ \begin{align*} H_x:=\{g\in G\mid T_gx=x\}. \end{align*} $$
$$ \begin{align*} H_x:=\{g\in G\mid T_gx=x\}. \end{align*} $$
 $(B_n,F_n)_{n=1}^\infty $
be the sequence of Rokhlin towers satisfying Definition 2.1(i). Fix a finite subset
$(B_n,F_n)_{n=1}^\infty $
be the sequence of Rokhlin towers satisfying Definition 2.1(i). Fix a finite subset
 $K\subset G\setminus \{1_G\}$
. Let
$K\subset G\setminus \{1_G\}$
. Let
 $F_n^K:=\{f\in F_n\mid Kf\subset F_n\}$
. Then, We let
$F_n^K:=\{f\in F_n\mid Kf\subset F_n\}$
. Then, We let $$ \begin{align*} \lim_{n\to\infty}\# F_n^K /\# F_n=1\quad\text{and}\quad \lim_{n\to\infty}\mu\bigg(\bigsqcup_{f\in F_n}T_fB_n\bigg)=1. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\# F_n^K /\# F_n=1\quad\text{and}\quad \lim_{n\to\infty}\mu\bigg(\bigsqcup_{f\in F_n}T_fB_n\bigg)=1. \end{align*} $$
 $X_n:=\bigsqcup _{f\in F_n^K}T_fB_n$
. Then,
$X_n:=\bigsqcup _{f\in F_n^K}T_fB_n$
. Then,
 $\mu (X_n)\to 1$
as
$\mu (X_n)\to 1$
as
 $n\to \infty $
. Hence,
$n\to \infty $
. Hence,
 $\mu $
-a.e. x belongs to
$\mu $
-a.e. x belongs to
 $X_n$
for some
$X_n$
for some
 $n=n(x)>0$
. It follows that the points
$n=n(x)>0$
. It follows that the points
 $T_kx$
,
$T_kx$
,
 $k\in K$
, belong to different levels of the tower
$k\in K$
, belong to different levels of the tower
 $(B_n,F_n)$
. Hence,
$(B_n,F_n)$
. Hence,
 $T_kx\ne x$
for each
$T_kx\ne x$
for each
 $k\in K$
, that is,
$k\in K$
, that is,
 $K\cap H_x=\emptyset $
. Since K is arbitrary, we conclude that
$K\cap H_x=\emptyset $
. Since K is arbitrary, we conclude that
 $H_x\cap G=\{1_g\}$
at a.e. x. Thus, T is free. Since
$H_x\cap G=\{1_g\}$
at a.e. x. Thus, T is free. Since
 $(F_n)_{n=1}^\infty $
is Følner, Definition 2.1(ii) is satisfied. Thus, T is of rank one according to Definition 2.1. The converse follows from Corollary 2.11(ii) and Theorem 2.13. Thus, we obtain that a probability preserving G-action T is of Følner rank-one if and only if T is of rank one according to Definition 2.1. Therefore, the main results of [Reference Johnson and McClendonJoMc]: their Theorems 3.1, 4.7 and 5.1 (which are stated for the Følner rank-one
$(F_n)_{n=1}^\infty $
is Følner, Definition 2.1(ii) is satisfied. Thus, T is of rank one according to Definition 2.1. The converse follows from Corollary 2.11(ii) and Theorem 2.13. Thus, we obtain that a probability preserving G-action T is of Følner rank-one if and only if T is of rank one according to Definition 2.1. Therefore, the main results of [Reference Johnson and McClendonJoMc]: their Theorems 3.1, 4.7 and 5.1 (which are stated for the Følner rank-one
 ${\mathbb Z}^d$
-actions) follow from our Theorems 3.3 and 5.4.
${\mathbb Z}^d$
-actions) follow from our Theorems 3.3 and 5.4.
-
(2) An ergodic G-action is totally ergodic if and only if it has no non-trivial finite factors. However, it is claimed in [Reference Johnson and McClendonJoMc, Theorem 3.3] that there exist non-totally ergodic Følner rank-one
 ${\mathbb Z}^2$
-actions without non-trivial finite factors. This seeming contradiction is caused by the non-standard definition of total ergodicity in [Reference Johnson and McClendonJoMc]. As we understood from the proof of [Reference Johnson and McClendonJoMc, Theorem 3.3], by the total ergodicity of a
${\mathbb Z}^2$
-actions without non-trivial finite factors. This seeming contradiction is caused by the non-standard definition of total ergodicity in [Reference Johnson and McClendonJoMc]. As we understood from the proof of [Reference Johnson and McClendonJoMc, Theorem 3.3], by the total ergodicity of a
 ${\mathbb Z}^d$
-action T, they mean the individual ergodicity of T, that is, that the transformation
${\mathbb Z}^d$
-action T, they mean the individual ergodicity of T, that is, that the transformation
 $T_g$
is ergodic for each non-zero
$T_g$
is ergodic for each non-zero
 $g\in {\mathbb Z}^d$
. The proof of [Reference Johnson and McClendonJoMc, Theorem 3.3] given there is based on their analysis of finite factors for rank-one systems. However, an easy alternative proof follows from the joining theory (see [Reference del Junco and RudolphdJRu, Reference RudolphRu]) and has no direct relation to the rank one. Indeed, let S be a transformation with MSJ. Let
$g\in {\mathbb Z}^d$
. The proof of [Reference Johnson and McClendonJoMc, Theorem 3.3] given there is based on their analysis of finite factors for rank-one systems. However, an easy alternative proof follows from the joining theory (see [Reference del Junco and RudolphdJRu, Reference RudolphRu]) and has no direct relation to the rank one. Indeed, let S be a transformation with MSJ. Let  be the space of S. Denote by T the following
be the space of S. Denote by T the following
 ${\mathbb Z}^2$
-action:
${\mathbb Z}^2$
-action:
 $T_{(n,m)}=S^n\times S^m$
,
$T_{(n,m)}=S^n\times S^m$
,
 $n,m\in {\mathbb Z}$
, on
$n,m\in {\mathbb Z}$
, on  . Of course, each factor of T is a factor of the transformation
. Of course, each factor of T is a factor of the transformation
 $T_{(1,1)}=S\times S$
. However,
$T_{(1,1)}=S\times S$
. However,
 $S\times S$
has only three non-trivial proper factors:
$S\times S$
has only three non-trivial proper factors:  ,
,  and
and  [Reference del Junco and RudolphdJRu]. The first two
[Reference del Junco and RudolphdJRu]. The first two
 $\sigma $
-algebras are also factors of T, while the latter one is not. Thus, T has only two proper factors which are weakly mixing. Hence, T is totally ergodic. Since
$\sigma $
-algebras are also factors of T, while the latter one is not. Thus, T has only two proper factors which are weakly mixing. Hence, T is totally ergodic. Since
 $T_{(1,0)}$
is not ergodic, T is not individually ergodic. It remains to note that the 3-cut Chacon transformation, used in the proof of [Reference Johnson and McClendonJoMc, Theorem 3.3], has MSJ [Reference del Junco, Rahe and SwansondJRaSw].
$T_{(1,0)}$
is not ergodic, T is not individually ergodic. It remains to note that the 3-cut Chacon transformation, used in the proof of [Reference Johnson and McClendonJoMc, Theorem 3.3], has MSJ [Reference del Junco, Rahe and SwansondJRaSw]. -
(3) Theorem 4.1 of [Reference Johnson and McClendonJoMc] is a particular case of our Theorem 4.9: G is amenable and the actions are probability preserving. Despite that, our proof of Theorem 4.9 is shorter than the proof of [Reference Johnson and McClendonJoMc, Theorem 4.1] because we use the Kőnig infinity lemma.
-
(4) Section 6 from [Reference Johnson and McClendonJoMc] is devoted entirely to construction of a
 ${\mathbb Z}^2$
-action T that has no
${\mathbb Z}^2$
-action T that has no
 ${\mathbb Z}^2$
-odometer factors but whose generators
${\mathbb Z}^2$
-odometer factors but whose generators
 $T_{(0,1)}$
and
$T_{(0,1)}$
and
 $T_{(1,0)}$
have
$T_{(1,0)}$
have
 ${\mathbb Z}$
-odometer factors. We provide a simpler construction in Example 6.4.
${\mathbb Z}$
-odometer factors. We provide a simpler construction in Example 6.4.
Acknowledgements
This work was supported in part by the ‘Long-term program of support of the Ukrainian research teams at the Polish Academy of Sciences carried out in collaboration with the U.S. National Academy of Sciences with the financial support of external partners' and by the Akhiezer Foundation. We thank R. Grigorchuk and A. Dudko for drawing our attention to Examples 4.5 and 4.6.





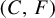
 of cofinite subgroups in
of cofinite subgroups in