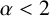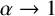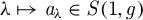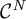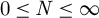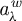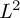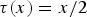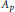Refine search
Actions for selected content:
9 results
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 172-183
- Print publication:
- August 2025
-
- Article
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of anisotropic Gabor wave front sets
- Part of
- Distributions, generalized functions, distribution spaces
- Miscellaneous topics - Partial differential equations
- Groups and semigroups of linear operators, their generalizations and applications
- Partial differential equations on manifolds; differential operators
- General quantum mechanics and problems of quantization
- Partial differential equations
- Integral, integro-differential, and pseudodifferential operators
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 674-698
-
- Article
- Export citation
Concentration phenomena for fractional magnetic NLS equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 28 May 2021, pp. 479-517
- Print publication:
- April 2022
-
- Article
- Export citation
EQUIVALENCE OF ELLIPTICITY AND THE FREDHOLM PROPERTY IN THE WEYL-HÖRMANDER CALCULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1363-1389
- Print publication:
- July 2022
-
- Article
- Export citation
Pseudo-differential operators with nonlinear quantizing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 103-130
- Print publication:
- February 2020
-
- Article
-
- You have access
- Open access
- Export citation
Multiplicity and concentration results for a fractional Schrödinger-Poisson type equation with magnetic field
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 655-694
- Print publication:
- April 2020
-
- Article
- Export citation
Decay estimates for solutions of nonlocal semilinear equations
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 175-198
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Weighted Lp Boundedness of Pseudodifferential Operators and Applications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 555-570
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation