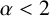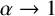1 Introduction
For a particle moving by way of Lévy flights, Laskin derived the Schrödinger equation with the kinetic energy operator represented by a fractional derivative [Reference Laskin7]. It was assumed that stochastic motion of the respective classical particle in one dimension is characterized by mean distance from the initial position growing with time as
![]() $|x|\sim t^{1/\alpha }$
, where
$|x|\sim t^{1/\alpha }$
, where
![]() $\alpha <2$
is the Lévy index (LI) [Reference Mandelbrot13]. After rescaling, the Schrödinger equation has the form
$\alpha <2$
is the Lévy index (LI) [Reference Mandelbrot13]. After rescaling, the Schrödinger equation has the form
 $$ \begin{align} i\frac{\partial \psi }{\partial t}=\frac{1}{2}\bigg( -\frac{\partial ^{2}}{ \partial x^{2}}\bigg) ^{\alpha /2}\psi , \end{align} $$
$$ \begin{align} i\frac{\partial \psi }{\partial t}=\frac{1}{2}\bigg( -\frac{\partial ^{2}}{ \partial x^{2}}\bigg) ^{\alpha /2}\psi , \end{align} $$
where the fractional operator represents the Riesz derivative [Reference Agrawal1],
 $$ \begin{align} \bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}\psi (x)= \frac{1}{2\pi }\int_{-\infty }^{+\infty }dp|p|^{\alpha }\int_{-\infty }^{+\infty }dx^{\prime }e^{ip(x-x^{\prime })}\psi (x^{\prime }). \end{align} $$
$$ \begin{align} \bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}\psi (x)= \frac{1}{2\pi }\int_{-\infty }^{+\infty }dp|p|^{\alpha }\int_{-\infty }^{+\infty }dx^{\prime }e^{ip(x-x^{\prime })}\psi (x^{\prime }). \end{align} $$
The fractional operator is constructed via the direct and inverse Fourier transforms incorporating fractional differentiation. In the limit of
![]() $\alpha =2$
, the operator (1.2) reduces to the usual second derivative.
$\alpha =2$
, the operator (1.2) reduces to the usual second derivative.
The fractional quantum mechanics description in terms of wave equations was also applied to Lévy crystals [Reference Stickler17] and polariton condensates [Reference Pinsker, Bao, Zhang, Ohadi, Dreismann and Baumberg16]. There were recent reports of experimental realization of the fractional group-velocity dispersion in a fibre-laser cavity [Reference Liu, Zhang, Malomed and Karimi9]. Theoretical models involving the fractional diffraction were extended to situations with external potentials (in particular, parity-time (
![]() $\mathcal {PT}$
) symmetric ones [Reference Zhang, Zhong, Belić, Zhu, Zhong, Zhang, Christodoulides and Xiao23]) and the Airy waves in two dimensions. In optical waveguide models, the fractional diffraction/dispersion is included in conjunction with the self-focusing Kerr nonlinearity leading to the fractional nonlinear Schrödinger equations (FNLSEs) [Reference Malomed12].
$\mathcal {PT}$
) symmetric ones [Reference Zhang, Zhong, Belić, Zhu, Zhong, Zhang, Christodoulides and Xiao23]) and the Airy waves in two dimensions. In optical waveguide models, the fractional diffraction/dispersion is included in conjunction with the self-focusing Kerr nonlinearity leading to the fractional nonlinear Schrödinger equations (FNLSEs) [Reference Malomed12].
The analyses of FNLSEs revealed the modulational instability of continuous waves [Reference Zhang, He, Conti, Wang, Hu, Lei, Li and Fan22], critical or supercritical collapse [Reference Chen, Zeng, Lu, Hu and Guo2] and other effects. Spontaneous symmetry breaking (SSB) in double-well potentials produced by self-trapping nonlinearity [Reference Malomed11] was studied in [Reference Davies3] and experimentally in [Reference Heil, Fischer, Elsässer, Mulet and Mirasso4] in various physical contexts. A recent focus of fractional diffraction was in the study of nonlinear systems with symmetric potentials [Reference Li and Dai8].
It is well known that SSB might arise in dual waveguides in the form of two-component solitons [Reference Malomed10]. Such a setting is relevant for modelling double-core optical fibres. In fibres, the SSB bifurcation of symmetric solitons into asymmetric two-component solitons was studied theoretically in a number of works including [Reference Wright, Stegeman and Wabnitz19], and it was demonstrated in an experiment [Reference Nguyen, Tai, Bugar, Longobucco, Buzcynski, Malomed and Trippenbach14]. In a recent work [Reference Zeng and Zeng21], families of symmetric and asymmetric solitons were found in the double-core system with fractional diffraction.
Recently, Strunin and Malomed [Reference Strunin and Malomed18] identified the SSB bifurcation of two- component solitons in the fractional dual-core waveguide. This was done both analytically, by means of the variational approximation (VA), and by systematic numerical computations. The comparison demonstrated that a relatively simple VA, based on the straightforward sech ansatz, produces quite accurate results. An essential finding was that deeper system’s fractionality (that is, smaller LI
![]() $\alpha $
in (1.2)) enhances the subcritical character [Reference Ioos and Joseph5] of the soliton bifurcation, which is its characteristic feature in the usual (nonfractional) double-core system [Reference Malomed10]. Thus, the fractionality makes the SSB of two-component solitons a more strongly pronounced phase transition of the first kind.
$\alpha $
in (1.2)) enhances the subcritical character [Reference Ioos and Joseph5] of the soliton bifurcation, which is its characteristic feature in the usual (nonfractional) double-core system [Reference Malomed10]. Thus, the fractionality makes the SSB of two-component solitons a more strongly pronounced phase transition of the first kind.
In this paper, we address the linearly coupled system of FNLSEs with the cubic self-focusing nonlinearity and the same fractional diffraction as in (1.1),
 $$ \begin{align} \begin{aligned} i\frac{\partial u_{1}}{\partial t} &=\frac{1}{2}\bigg( -\frac{\partial ^{2} }{\partial x^{2}}\bigg) ^{\alpha /2}u_{1}-|u_{1}|^{2}u_{1}-u_{2}, \\ i\frac{\partial u_{2}}{\partial t} &=\frac{1}{2}\bigg( -\frac{\partial ^{2} }{\partial x^{2}}\bigg) ^{\alpha /2}u_{2}-|u_{2}|^{2}u_{2}-u_{1}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} i\frac{\partial u_{1}}{\partial t} &=\frac{1}{2}\bigg( -\frac{\partial ^{2} }{\partial x^{2}}\bigg) ^{\alpha /2}u_{1}-|u_{1}|^{2}u_{1}-u_{2}, \\ i\frac{\partial u_{2}}{\partial t} &=\frac{1}{2}\bigg( -\frac{\partial ^{2} }{\partial x^{2}}\bigg) ^{\alpha /2}u_{2}-|u_{2}|^{2}u_{2}-u_{1}, \end{aligned} \end{align} $$
where the coupling coefficient in front of terms (
![]() $-u_{2}$
) and (
$-u_{2}$
) and (
![]() $-u_{1}$
) in the first and second equations is set to be
$-u_{1}$
) in the first and second equations is set to be
![]() $1$
by means of scaling. The only irreducible control parameter of the normalized system (1.3) is LI
$1$
by means of scaling. The only irreducible control parameter of the normalized system (1.3) is LI
![]() $\alpha $
, and intrinsic parameters of soliton solutions will be the propagation constant k and velocity (tilt) c (see (2.1) and (2.4) below). Throughout the paper, we call solutions with equal components,
$\alpha $
, and intrinsic parameters of soliton solutions will be the propagation constant k and velocity (tilt) c (see (2.1) and (2.4) below). Throughout the paper, we call solutions with equal components,
![]() $u_{1}$
=
$u_{1}$
=
![]() $u_{2}$
, symmetric. Solutions with unequal components are called asymmetric.
$u_{2}$
, symmetric. Solutions with unequal components are called asymmetric.
The paper is organized as follows: the framework for the construction of soliton solutions, and analysis of their stability and dynamics are presented in Section 2; numerical results, for quiescent and moving solitons, are summarized in Section 3; the conclusion is given in Section 4.
2 Soliton solutions
Stationary solutions to (1.3) with propagation constant k are looked for in the form
with real functions
![]() $u_{1,2}(x)$
. These solutions must satisfy
$u_{1,2}(x)$
. These solutions must satisfy
 $$ \begin{align} \begin{aligned} kU_{1}+\frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}U_{1}-U_{1}^{3}-U_{2} &=0, \\ kU_{2}+\frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}U_{2}-U_{2}^{3}-U_{1} &=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} kU_{1}+\frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}U_{1}-U_{1}^{3}-U_{2} &=0, \\ kU_{2}+\frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial x^{2}}\bigg) ^{\alpha /2}U_{2}-U_{2}^{3}-U_{1} &=0. \end{aligned} \end{align} $$
As is well established, the single one-dimensional FNLSE generates stable solitons for
while at
![]() $\alpha \leq 1$
, the solitons are unstable because of the collapse [Reference Malomed12], and hence we consider values of LI belonging to interval (2.3) as was done in [Reference Strunin and Malomed18].
$\alpha \leq 1$
, the solitons are unstable because of the collapse [Reference Malomed12], and hence we consider values of LI belonging to interval (2.3) as was done in [Reference Strunin and Malomed18].
In the case of the usual diffraction,
![]() $\alpha =2$
, a simple solution of (2.2) in the form of symmetric solitons is
$\alpha =2$
, a simple solution of (2.2) in the form of symmetric solitons is
The norm (power) of this solution is
 $$ \begin{align*} N=\int_{-\infty }^{+\infty }[ ( U_{1}(x)) ^{2}+( U_{2}(x)) ^{2}]\,dx=4\sqrt{2( k-1) }. \end{align*} $$
$$ \begin{align*} N=\int_{-\infty }^{+\infty }[ ( U_{1}(x)) ^{2}+( U_{2}(x)) ^{2}]\,dx=4\sqrt{2( k-1) }. \end{align*} $$
With the increase of N, the symmetric states become unstable through SSB, and stable asymmetric solitons appear. The SSB is caused by the lowest energy level achieved through asymmetric solution, which manifests itself as a new ground state of the system. While there are no exact solutions for the asymmetric solitons, the SSB point, at which they emerge, can be found exactly for
![]() $\alpha =2$
[Reference Wright, Stegeman and Wabnitz19]:
$\alpha =2$
[Reference Wright, Stegeman and Wabnitz19]:
Strunin and Malomed [Reference Strunin and Malomed18] confirmed this criterion to a high accuracy.
Solutions of (1.3) for solitons moving with speed c are sought for as
In terms of
![]() $( \xi ,t) $
, (1.3) take the form
$( \xi ,t) $
, (1.3) take the form
 $$ \begin{align} \begin{aligned} i\frac{\partial u_{1}}{\partial t}-ic\frac{\partial u_{1}}{\partial \xi } &= \frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial \xi ^{2}}\bigg) ^{\alpha /2}u_{1}-|u_{1}|^{2}u_{1}-u_{2}, \\ i\frac{\partial u_{2}}{\partial t}-ic\frac{\partial u_{2}}{\partial \xi } &= \frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial \xi ^{2}}\bigg) ^{\alpha /2}u_{2}-|u_{2}|^{2}u_{2}-u_{1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} i\frac{\partial u_{1}}{\partial t}-ic\frac{\partial u_{1}}{\partial \xi } &= \frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial \xi ^{2}}\bigg) ^{\alpha /2}u_{1}-|u_{1}|^{2}u_{1}-u_{2}, \\ i\frac{\partial u_{2}}{\partial t}-ic\frac{\partial u_{2}}{\partial \xi } &= \frac{1}{2}\bigg( -\frac{\partial ^{2}}{\partial \xi ^{2}}\bigg) ^{\alpha /2}u_{2}-|u_{2}|^{2}u_{2}-u_{1}. \end{aligned} \end{align} $$
Solutions to (2.5) are further looked for as
![]() $u_{1,2}( \xi ,t) = U_{1,2}(\xi )e^{ikt}$
[see (2.1)], with complex functions
$u_{1,2}( \xi ,t) = U_{1,2}(\xi )e^{ikt}$
[see (2.1)], with complex functions
![]() $U_{1,2}(\xi )$
satisfying the system of stationary equations
$U_{1,2}(\xi )$
satisfying the system of stationary equations
 $$ \begin{align} \begin{aligned} kU_{1}+ic\frac{dU_{1}}{d\xi }+\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}U_{1}-\vert U_{1}\vert ^{2}U_{1}-U_{2} &=0,\\ kU_{2}+ic\frac{dU_{2}}{d\xi }+\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}U_{2}-\vert U_{2}\vert ^{2}U_{2}-U_{1} &=0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} kU_{1}+ic\frac{dU_{1}}{d\xi }+\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}U_{1}-\vert U_{1}\vert ^{2}U_{1}-U_{2} &=0,\\ kU_{2}+ic\frac{dU_{2}}{d\xi }+\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}U_{2}-\vert U_{2}\vert ^{2}U_{2}-U_{1} &=0. \end{aligned} \end{align} $$

Figure 1 (a) The stationary profile of a stable symmetric soliton, (b) the respective spectrum of perturbation eigenvalues and (c) perturbed evolution of the soliton, for
![]() $ \alpha =1.6$
,
$ \alpha =1.6$
,
![]() $k=1.5$
and
$k=1.5$
and
![]() $N=3.721$
. The amplitudes
$N=3.721$
. The amplitudes
![]() $U_{1}(x)$
(blue line) and
$U_{1}(x)$
(blue line) and
![]() $U_{2}(x)$
(red circles) are shown in panel (a); the functions
$U_{2}(x)$
(red circles) are shown in panel (a); the functions
![]() $\vert u_{1}(x,t)\vert $
and
$\vert u_{1}(x,t)\vert $
and
![]() $\vert u_{2}(x,t)\vert $
are shown in panel (c). Similar labels are used in Figures 2 and 3.
$\vert u_{2}(x,t)\vert $
are shown in panel (c). Similar labels are used in Figures 2 and 3.
The stability of solitons is analysed by considering solutions including small perturbations
![]() $a_{1,2}$
and
$a_{1,2}$
and
![]() $b_{1,2}$
,
$b_{1,2}$
,
where
![]() $\lambda $
is the eigenvalue with real part Re
$\lambda $
is the eigenvalue with real part Re
![]() $( \lambda )$
responsible for the growth/decay rate, and
$( \lambda )$
responsible for the growth/decay rate, and
![]() $\ast $
stands for the complex conjugate. The linearization of (1.3) for the perturbations leads to the system of Bogoliubov–de Gennes (BdG) equations:
$\ast $
stands for the complex conjugate. The linearization of (1.3) for the perturbations leads to the system of Bogoliubov–de Gennes (BdG) equations:
 $$ \begin{align} \begin{aligned} &[ -( k-i\lambda ) -\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}+2\vert U_{1,2}\vert ^{2}\bigg] a_{1,2}+U_{1,2}^{2}b_{1,2}+a_{2,1} =0, \\ &\bigg[ -( k+i\lambda ) -\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}+2\vert U_{1,2}\vert ^{2}\bigg] b_{1,2}+( U_{1,2}^{\ast }) ^{2}a_{1,2}+b_{2,1} =0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &[ -( k-i\lambda ) -\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}+2\vert U_{1,2}\vert ^{2}\bigg] a_{1,2}+U_{1,2}^{2}b_{1,2}+a_{2,1} =0, \\ &\bigg[ -( k+i\lambda ) -\frac{1}{2}\bigg( -\frac{d^{2}}{d\xi ^{2}} \bigg) ^{\alpha /2}+2\vert U_{1,2}\vert ^{2}\bigg] b_{1,2}+( U_{1,2}^{\ast }) ^{2}a_{1,2}+b_{2,1} =0. \end{aligned} \end{align} $$
The BdG equations can be straightforwardly updated for the moving soliton case (
![]() $c>0$
). The solitons are (neutrally) stable, if solutions of (2.7) produce only eigenvalues with Re
$c>0$
). The solitons are (neutrally) stable, if solutions of (2.7) produce only eigenvalues with Re
![]() $( \lambda ) =0$
[Reference Yang20]. We support the stability outcome derived from the BdG equations, by direct simulations of the evolution of perturbed solitons.
$( \lambda ) =0$
[Reference Yang20]. We support the stability outcome derived from the BdG equations, by direct simulations of the evolution of perturbed solitons.
3 Numerical simulations
First, we present some typical results for the quiescent soliton solutions and their stability. Soliton solutions of (2.2) are obtained by the squared-operator iteration method [Reference Yang20]. The stability eigenvalues
![]() $\lambda $
are computed by solving (2.7) using the Fourier collocation method. Both algorithms were realized in Matlab [Reference Yang20]. When implementing the Fourier collocation method, we represented the functions of interest as Fourier series [Reference Strunin and Malomed18], which was convenient for our purposes, as the action of fractional derivative (1.2) in the Fourier space amounts to multiplication by factor
$\lambda $
are computed by solving (2.7) using the Fourier collocation method. Both algorithms were realized in Matlab [Reference Yang20]. When implementing the Fourier collocation method, we represented the functions of interest as Fourier series [Reference Strunin and Malomed18], which was convenient for our purposes, as the action of fractional derivative (1.2) in the Fourier space amounts to multiplication by factor
![]() $|p|^{\alpha }$
. Direct simulations of (1.3) are performed by means of the pseudospectral method [Reference Yang20], based on the discrete Fourier transform and the Runge–Kutta time-stepping method.
$|p|^{\alpha }$
. Direct simulations of (1.3) are performed by means of the pseudospectral method [Reference Yang20], based on the discrete Fourier transform and the Runge–Kutta time-stepping method.
Strunin and Malomed [Reference Strunin and Malomed18] presented an example of unstable asymmetric solitons. In Figures 1, 2 and 3, we show typical examples of stable and unstable symmetric solitons and stable asymmetric solitons. The latter lead to particularly interesting collision results as described further below. Each figure displays profiles of two components of the stationary solution, the spectrum of its stability eigenvalues (recall the stability implies that all eigenvalues must have zero real parts) and direct simulations of the perturbed evolution of the solitons.

Figure 2 The same as in Figure 1, but for an unstable symmetric soliton, with
![]() $ \alpha =1.6$
,
$ \alpha =1.6$
,
![]() $k=1.8$
and
$k=1.8$
and
![]() $N=4.438 $
.
$N=4.438 $
.

Figure 3 The same as in Figure 1, but for a stable asymmetric soliton, with
![]() $ \alpha =1.6$
,
$ \alpha =1.6$
,
![]() $k=2.5$
and
$k=2.5$
and
![]() $N=3.726$
.
$N=3.726$
.
From Figure 2, we observe that the instability of the symmetric soliton spontaneously turns it into an asymmetric one, with residual internal oscillations. Shortly after the start of the dynamic, one of the components, namely
![]() $u_{1}$
in this case, increases due to the positive eigenvalue, while
$u_{1}$
in this case, increases due to the positive eigenvalue, while
![]() $u_{2}$
decreases due to the negative eigenvalue.
$u_{2}$
decreases due to the negative eigenvalue.
Once moving stable solitons are produced, they can be used to explore collisions of soliton pairs. For this purpose, two solitons were numerically constructed as solutions of (2.6),
![]() $u_{1,2}^{\pm }$
, with velocities
$u_{1,2}^{\pm }$
, with velocities
![]() $\pm c$
. Then, direct simulations of (1.3) are run, with the input in the form of the pair of solitons
$\pm c$
. Then, direct simulations of (1.3) are run, with the input in the form of the pair of solitons
![]() $u_{1,2}^{\pm }(x)$
placed respectively at
$u_{1,2}^{\pm }(x)$
placed respectively at
![]() $x<0$
and
$x<0$
and
![]() $x>0$
, with a sufficiently large distance between them.
$x>0$
, with a sufficiently large distance between them.
In this paper, we focus on the collisions between mutually symmetric solitons, with equal values of the propagation constant, k: (1) two stable symmetric solitons; (2) two stable asymmetric solitons, with the same k, in the flipped configuration, where soliton
![]() $u_{1,2}^{+}$
has a larger component
$u_{1,2}^{+}$
has a larger component
![]() $u_{1}$
and a smaller one
$u_{1}$
and a smaller one
![]() $u_{2} $
, and vice versa for
$u_{2} $
, and vice versa for
![]() $u_{1,2}^{-}$
(see [Reference Peng, Malomed and Chu15]).
$u_{1,2}^{-}$
(see [Reference Peng, Malomed and Chu15]).
In [Reference Strunin and Malomed18], the outcomes of collisions between stable symmetric solitons, at gradually increasing speeds
![]() $\pm c$
, were presented. In all cases, the colliding solitons bounced back – naturally, remaining far separated for smallest speeds and approaching closer to each other for larger c. Up to
$\pm c$
, were presented. In all cases, the colliding solitons bounced back – naturally, remaining far separated for smallest speeds and approaching closer to each other for larger c. Up to
![]() $c=0.06$
, the entire picture remains fully symmetric, with respect to both the two components in each soliton and the two colliding solitons as well. Next, starting from
$c=0.06$
, the entire picture remains fully symmetric, with respect to both the two components in each soliton and the two colliding solitons as well. Next, starting from
![]() $c=0.08$
, the simulations demonstrated the onset of collision-induced SSB, which became obvious at
$c=0.08$
, the simulations demonstrated the onset of collision-induced SSB, which became obvious at
![]() $c=0.10$
. In the latter case, the collision broke the symmetry between the components, as well as between the colliding solitons. It is worth noting that the post-collision amplitude of component
$c=0.10$
. In the latter case, the collision broke the symmetry between the components, as well as between the colliding solitons. It is worth noting that the post-collision amplitude of component
![]() $u_{2}$
in the left soliton is much larger than before the collision. The collision-induced SSB effect was explained by the instability of the transient state formed by the colliding solitons when they are separated by a relatively small distance.
$u_{2}$
in the left soliton is much larger than before the collision. The collision-induced SSB effect was explained by the instability of the transient state formed by the colliding solitons when they are separated by a relatively small distance.
In the present paper, our main interest is the collisions at significantly higher speeds [Reference Kivshar and Malomed6]. We observe an interesting effect of restoration of symmetry as illustrated in Figure 4. The restoration is observed starting from
![]() $c=0.34$
. At the highest speed presented,
$c=0.34$
. At the highest speed presented,
![]() $c=0.40$
, the collision is seen to be fully elastic, with the post-collision solitons being identical to their counterparts before the collision.
$c=0.40$
, the collision is seen to be fully elastic, with the post-collision solitons being identical to their counterparts before the collision.

Figure 4 Gradual restoration of the symmetry at high speeds in collisions of symmetric solitons for
![]() $ \alpha =1.6$
,
$ \alpha =1.6$
,
![]() $k=1.4$
. The norm of each soliton is
$k=1.4$
. The norm of each soliton is
![]() $N=3.303$
(
$N=3.303$
(
![]() $c=0.2$
),
$c=0.2$
),
![]() $N=3.152$
(
$N=3.152$
(
![]() $c=0.3$
),
$c=0.3$
),
![]() $N=3.075$
(
$N=3.075$
(
![]() $c=0.34$
),
$c=0.34$
),
![]() $N=2.939$
(
$N=2.939$
(
![]() $c=0.4$
).
$c=0.4$
).
Next, in Figure 5, we demonstrate results of collisions between stable asymmetric solitons in the flipped state, as defined above. The general picture is similar to that outlined above for the collisions between symmetric solitons. Namely, at low speeds,
![]() $c\leq 0.04$
, the solitons bounce back, without breaking the symmetry between the colliding ones. In fact, in this case, each soliton switches from the intrinsic asymmetric shape into a nearly symmetric one, as concerns the relation between its two components. Then, starting from
$c\leq 0.04$
, the solitons bounce back, without breaking the symmetry between the colliding ones. In fact, in this case, each soliton switches from the intrinsic asymmetric shape into a nearly symmetric one, as concerns the relation between its two components. Then, starting from
![]() $c=0.06$
, the collision-induced SSB effect sets in, leading to strong symmetry breaking at
$c=0.06$
, the collision-induced SSB effect sets in, leading to strong symmetry breaking at
![]() $c=0.1$
, with a dominant
$c=0.1$
, with a dominant
![]() $u_{1}$
component of the left soliton in the post-collision state. Then, Figure 5 demonstrates that strong SSB persists, with the increase of the speed, up to
$u_{1}$
component of the left soliton in the post-collision state. Then, Figure 5 demonstrates that strong SSB persists, with the increase of the speed, up to
![]() $c=0.40$
. Starting from
$c=0.40$
. Starting from
![]() $c=0.60$
, the further increase of the speed gradually leads to the restoration of the symmetry between the colliding solitons and at the speed
$c=0.60$
, the further increase of the speed gradually leads to the restoration of the symmetry between the colliding solitons and at the speed
![]() $c=0.80$
, the collision appears to be quasi-elastic.
$c=0.80$
, the collision appears to be quasi-elastic.

Figure 5 Gradual restoration of the symmetry at high speeds in collisions of the mutually flipped asymmetric solitons for
![]() $ \alpha =1.6$
,
$ \alpha =1.6$
,
![]() $k=2.6 $
. The norm of each soliton is
$k=2.6 $
. The norm of each soliton is
![]() $N=3.638$
(
$N=3.638$
(
![]() $c=0.4$
),
$c=0.4$
),
![]() $N=3.576$
(
$N=3.576$
(
![]() $c=0.5$
),
$c=0.5$
),
![]() $N=3.500$
(
$N=3.500$
(
![]() $c=0.6$
),
$c=0.6$
),
![]() $N=3.483$
(
$N=3.483$
(
![]() $c=0.62$
),
$c=0.62$
),
![]() $N=3.466$
(
$N=3.466$
(
![]() $c=0.64$
),
$c=0.64$
),
![]() $N=3.312$
(
$N=3.312$
(
![]() $c=0.80$
).
$c=0.80$
).
4 Conclusion
We analysed solitons in systems with fractional diffraction, especially the SSB (spontaneous symmetry breaking) in the one-dimensional dual-core configuration. The systems involve the Riesz fractional derivative, cubic self-focusing acting in the cores and inter-core linear coupling. The corresponding system of FNLSEs (fractional nonlinear Schrödinger equations) models tunnel-coupled planar optical waveguides with the fractional diffraction, as well as coupled waveguides with the fractional group-velocity dispersion in the temporal domain [Reference Liu, Zhang, Malomed and Karimi9]. Using numerical methods, we obtained static and moving solitons of symmetric and asymmetric shapes. Collisions between the moving solitons are explored, demonstrating restoration of symmetry at high soliton speeds.
Acknowledgement
The work of B. A. Malomed was supported, in part, by Grant No. 1695/22 of the Israel Science Foundation.