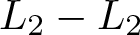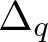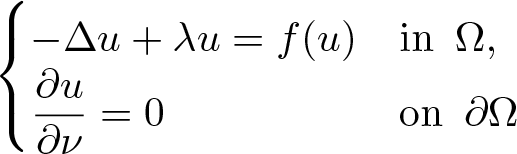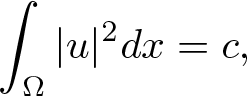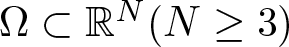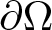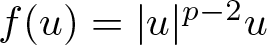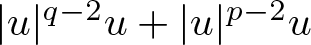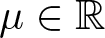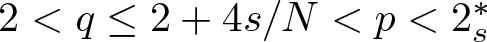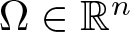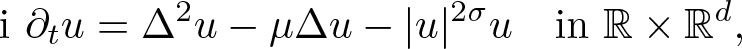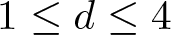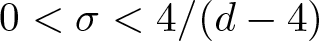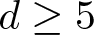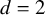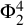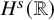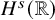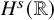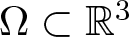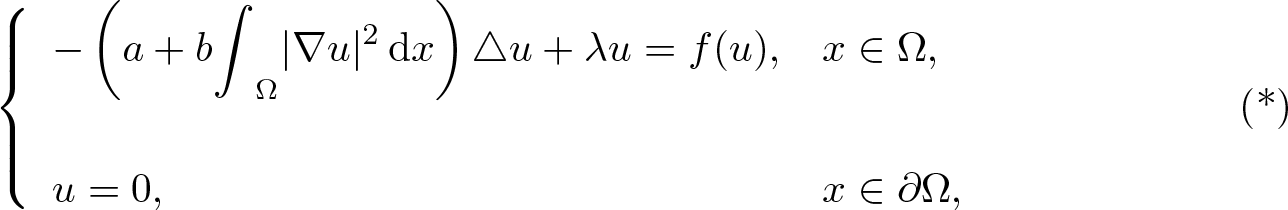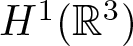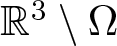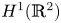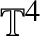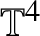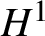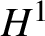Refine search
Actions for selected content:
76 results
Global solutions to 3D quadratic nonlinear Schrödinger-type equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 November 2025, e183
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative quasi-invariance of Gaussian measures below the energy level for the 1D generalized nonlinear Schrödinger equation and application to global well-posedness
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-33
-
- Article
- Export citation
Local well-posedness and blow-up in the energy space for the 2D NLS with point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-20
-
- Article
- Export citation
Regular solutions to the dissipative Aw–Rascle system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity criteria for the 3D Navier–Stokes and MHD equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1262-1296
-
- Article
- Export citation
Remark on the local well-posedness for NLS with the modulated dispersion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-12
-
- Article
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
- Export citation
Radial solutions of initial boundary value problems of nonlinear Schrödinger equations in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Blowup of cylindrically symmetric solutions for biharmonic NLS
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1085-1098
-
- Article
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp well-posedness for the cubic NLS and mKdV in
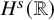 $H^s({{\mathbb {R}}})$
$H^s({{\mathbb {R}}})$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1938-1959
- Print publication:
- October 2025
-
- Article
- Export citation
A NOTE ON NORMALISED GROUND STATES FOR THE TWO-DIMENSIONAL CUBIC-QUINTIC NONLINEAR SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 552-561
- Print publication:
- June 2024
-
- Article
- Export citation
Groundstates of the planar Schrödinger–Poisson system with potential well and lack of symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 993-1023
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of positive solutions for Kirchhoff-type problem in exterior domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 182-217
-
- Article
- Export citation
Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 279-301
-
- Article
- Export citation
Resonance-based schemes for dispersive equations via decorated trees
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unconditional uniqueness for the energy-critical nonlinear Schrödinger equation on
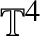 $\mathbb {T}^{4}$
$\mathbb {T}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation