Refine search
Actions for selected content:
13 results
Shrinking vs. expanding: the evolution of spatial support in degenerate Keller–Segel systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
- Export citation
Adhesion and volume filling in one-dimensional population dynamics under Dirichlet boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1174-1222
- Print publication:
- August 2025
-
- Article
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW NONLOCAL NONLINEAR DIFFUSION EQUATION: THE ONE-DIMENSIONAL CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 05 May 2022, pp. 333-339
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a repulsion Keller–Segel system with a logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 153-181
-
- Article
- Export citation
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 937-982
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Gradient Estimates for Spacelike Mean Curvature Flow with Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 459-469
-
- Article
- Export citation
Evolution of non-simple closed curves in the area-preserving curvature flow
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 659-668
- Print publication:
- June 2018
-
- Article
- Export citation
Uniqueness of the null solution to a nonlinear partial differential equation satisfied by the explosion probability of a branching diffusion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 938-945
- Print publication:
- September 2016
-
- Article
- Export citation
GEOMETRIC SYMMETRY TECHNIQUES FOR PARTIAL DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 342-344
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
On a class of nonlinear anisotropic parabolic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1-21
- Print publication:
- February 2016
-
- Article
- Export citation
A Bistable Field Model of Cancer Dynamics
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1-18
- Print publication:
- January 2012
-
- Article
- Export citation

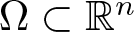
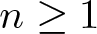
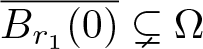
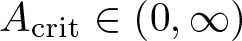
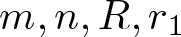

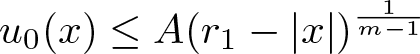


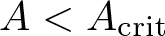
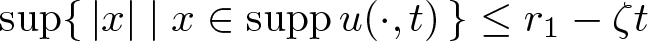
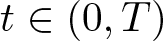
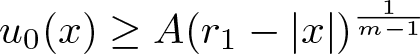
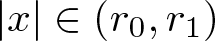
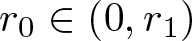

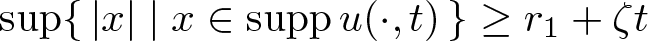
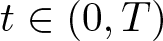
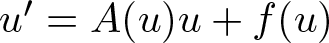
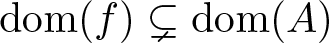
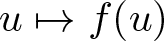
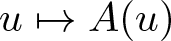
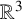
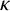
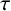
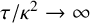
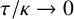
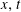
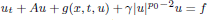
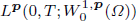 , where the data
, where the data 