Refine search
Actions for selected content:
8 results
A reinterpretation of set differential equations as differential equations in a Banach space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 November 2017, pp. 429-446
- Print publication:
- April 2018
-
- Article
- Export citation
Application of Measure of Noncompactness to Infinite Systems of Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 388-394
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
BOUNDARY VALUE PROBLEMS VIA AN INTERMEDIATE VALUE THEOREM
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 01 September 2008, pp. 531-537
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
ON POINTWISE ONE-SIDED ESTIMATES FOR CONTINUOUS FUNCTIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 48 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 24 March 2006, pp. 83-91
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation
LINEAR DETERMINING EQUATIONS FOR DIFFERENTIAL CONSTRAINTS
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue A / June 2005
- Published online by Cambridge University Press:
- 14 July 2005, pp. 109-120
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Abstract Cauchy problems for quasi-linear evolution equations in the sense of Hadamard
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 89 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 30 June 2004, pp. 123-160
- Print publication:
- July 2004
-
- Article
- Export citation
Deterministic approximation of a stochastic metapopulation model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 691-720
- Print publication:
- September 2003
-
- Article
- Export citation
Asymptotic behaviour of non-autonomous dissipative systems in Hilbert space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 93-103
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
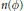
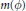
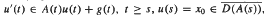 where {
where {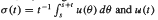 are weakly convergent.
are weakly convergent.