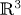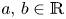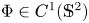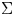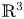Refine search
Actions for selected content:
3 results
Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$
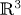
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1347-1370
- Print publication:
- August 2023
-
- Article
- Export citation
Adapted Nested Force-Gradient Integrators: The Schwinger Model Case
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 1141-1153
- Print publication:
- April 2017
-
- Article
- Export citation
The Geometry of Quadratic Differential Systems with a Weak Focus of Third Order
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 2 / 01 April 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-343
- Print publication:
- 01 April 2004
-
- Article
-
- You have access
- Export citation