Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T03:27:11.081Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$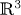

Part of: Classical differential geometry Global differential geometry Qualitative theory

Published online by Cambridge University Press:  22 July 2022

Antonio Bueno  and
Irene Ortiz
Antonio Bueno
Affiliation:
Departamento de Ciencias, Centro Universitario de la Defensa de San Javier, E-30729 Santiago de la Ribera, Spain (antonio.bueno@cud.upct.es, irene.ortiz@cud.upct.es)
Irene Ortiz
Affiliation:
Departamento de Ciencias, Centro Universitario de la Defensa de San Javier, E-30729 Santiago de la Ribera, Spain (antonio.bueno@cud.upct.es, irene.ortiz@cud.upct.es)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given $a,\,b\in \mathbb {R}$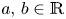 and $\Phi \in C^{1}(\mathbb {S}^{2})$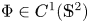, we study immersed oriented surfaces $\Sigma$ 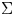in the Euclidean 3-space $\mathbb {R}^{3}$ 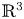whose mean curvature $H$ 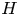and Gauss curvature $K$ 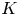satisfy $2aH+bK=\Phi (N)$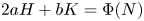, where $N:\Sigma \rightarrow \mathbb {S}^{2}$ 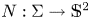is the Gauss map. This theory widely generalizes some of paramount importance such as the ones constant mean and Gauss curvature surfaces, linear Weingarten surfaces and self-translating solitons of the mean curvature flow. Under mild assumptions on the prescribed function $\Phi$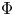, we exhibit a classification result for rotational surfaces in the case that the underlying fully nonlinear PDE that governs these surfaces is elliptic or hyperbolic.

Keywords

Prescribed Weingarten curvaturelinear Weingarten surfacerotational surfacenonlinear autonomous systemphase plane analysis

MSC classification

Primary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.) 34C05: Location of integral curves, singular points, limit cycles 34C40: Equations and systems on manifolds

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1347 - 1370
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This paper is dedicated to the first author's mother, whose daily fight, strength and spirit of overcoming adversity prove that there are way more difficult and important issues in life than a mathematical problem

References

Alexandrov, A. D.. Uniqueness theorems for surfaces in the large. I, Vestnik Leningrad Univ. 11 (1956), 5–17. (English translation): Amer. Math. Soc. Transl. 21 (1962), 341–354.Google Scholar
Bueno, A.. A Delaunay-type classification result for prescribed mean curvature surfaces in $\mathbb {M}^{2}(\kappa )\times \mathbb {R}$. Pacific J. Math. 313 (2021), 45–74.CrossRefGoogle Scholar
Bueno, A.. Delaunay surfaces of prescribed mean curvature in Berger spheres. J. Geom. Phys. 171 (2022), 104412.Google Scholar
Bueno, A.. Delaunay surfaces of prescribed mean curvature in $\mathrm {Nil}_3$ and $\widetilde {Sl}_2(\mathbb {R})$. J. Geom. Anal. 32 (2022), 196.CrossRefGoogle Scholar
Bueno, A. and López, R.. Radial solutions for equations of Weingarten type, preprint arXiv:2201.06474.Google Scholar
Bueno, A. and Ortiz, I.. Rotational surfaces of prescribed Gauss curvature in $\mathbb {R}^{3}$, to appear in Tohoku Math. Journal.Google Scholar
Bueno, A., Gálvez, J. A. and Mira, P.. Rotational hypersurfaces of prescribed mean curvature. J. Differ. Equ. 268 (2020), 2394–2413.CrossRefGoogle Scholar
Bueno, A., Gálvez, J. A. and Mira, P.. The global geometry of surfaces with prescribed mean curvature in $\mathbb {R}^{3}$. Trans. Amer. Math. Soc. 373 (2020), 4437–4467.Google Scholar
Chern, S. S.. (1955) On special $W$-surfaces. Proc. Amer. Math. Soc. 6 (1955), 783–786.Google Scholar
Christoffel, E. B.. Über die Bestimmung der Gestalt einer krummen Oberfläche durch lokale Messungen auf derselben. J. Reine Angew. Math. 64 (1865), 193–209.Google Scholar
Clutterbuck, J., Schnurer, O. and Schulze, F.. Stability of translating solutions to mean curvature flow. Calc. Var. Partial Diff. Equ. 29 (2007), 281–293.Google Scholar
Gálvez, J. A., Martínez, A. and Milán, F.. Linear Weingarten Surfaces in $\mathbb {R}^{3}$. Monatsh. Math. 138 (2003), 133–144.CrossRefGoogle Scholar
Gálvez, J. A. and Mira, P.. A Hopf theorem for non-constant mean curvature and a conjecture of A.D. Alexandrov. Math. Ann. 366 (2016), 909–928.CrossRefGoogle Scholar
Gálvez, J. A. and Mira, P.. Uniqueness of immersed spheres in three-manifolds. J. Differ. Geometry 116 (2020), 459–480.CrossRefGoogle Scholar
Gomes, J. M.. Spherical surfaces with constant mean curvature in hyperbolic space. Bol. Soc. Bras. Math. 18 (1987), 49–73.CrossRefGoogle Scholar
Guan, B. and Guan, P.. Convex hypersurfaces of prescribed curvatures. Ann. Math. 156 (2002), 655–673.Google Scholar
Hartman, P. and Wintner, A.. On the third fundamental form of a surface. Amer. J. Math. 75 (1953), 298–334.CrossRefGoogle Scholar
Hartman, P. and Wintner, W.. Umbilical points and $W$-surfaces. Amer. J. Math. 76 (1954), 502–508.CrossRefGoogle Scholar
Hopf, H.. Differential Geometry in the Large. Lecture Notes in Math, Vol. 1000, Berlin: Springer-Verlag, 1982.Google Scholar
Huisken, G. and Sinestrari, C.. Convexity estimates for mean curvature flow and singularities of mean convex surfaces. Acta Math. 183 (1993), 45–70.Google Scholar
Ilmanen, T.. Elliptic regularization and partial regularity for motion by mean curvature, Mem. Amer. Math. Soc. Vol. 108 (1994).Google Scholar
López, R.. Rotational linear Weingarten surfaces of hyperbolic type. Israel J. Math. 167 (2008), 283–302.CrossRefGoogle Scholar
López, R.. Invariant surfaces in Euclidean space with a log-linear density. Adv. Math. 339 (2018), 285–309.CrossRefGoogle Scholar
Martín, F., Savas-Halilaj, A. and Smoczyk, K.. On the topology of translating solitons of the mean curvature flow. Calc. Var. Partial Diff. Equ. 54 (2015), 2853–2882.CrossRefGoogle Scholar
Minkowski, H.. Volumen und Oberfläche. Math. Ann. 57 (1903), 447–495.CrossRefGoogle Scholar
Pogorelov, A. V.. Extension of a general uniqueness theorem of A.D. Aleksandrov to the case of nonanalytic surfaces (in Russian). Doklady Akad. Nauk SSSR 62 (1948), 297–299.Google Scholar
Rosenberg, H. and Sa Earp, R.. The geometry of properly embedded special surfaces in $\mathbb {R}^{3}$; e.g., surfaces satisfying $aH+bK=1$, where $a$ and $b$ are positive. Duke Math. J. 73 (1994), 291–306.CrossRefGoogle Scholar
Sa Earp, R. and Toubiana, E.. Surfaces de Weingarten speciales de type minimal. Bol. Soc. Brasil. Mat. 26 (1995), 129–148.CrossRefGoogle Scholar
Sa Earp, R. and Toubiana, E.. Classification des surfaces de type Delaunay. Amer. J. Math. 121 (1999), 671–700.CrossRefGoogle Scholar