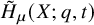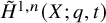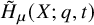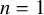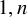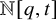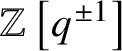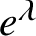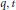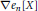Refine search
Actions for selected content:
4 results
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A raising operator formula for Macdonald polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse K-Chevalley formulas for semi-infinite flag manifolds, I: minuscule weights in ADE type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Compositional Shuffle Conjecture Specifying Touch Points of the Dyck Path
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 4 / 01 August 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 822-844
- Print publication:
- 01 August 2012
-
- Article
-
- You have access
- Export citation