We showbymeans of an example in ${{\mathbb{C}}^{3}}$ that Gromov’s theoremon the presence of attached holomorphic discs for compact Lagrangianmanifolds is not true in the subcritical real-analytic case, even in the absence of an obvious obstruction, i.e., polynomial convexity.

Given a real analytic set $X$ in a complex manifold and a positive integer $d$, denote by ${{\mathcal{A}}^{d}}$ the set of points $p$ in $X$ at which there exists a germ of a complex analytic set of dimension $d$ contained in $X$. It is proved that ${{\mathcal{A}}^{d}}$ is a closed semianalytic subset of $X$.

In this paper we construct analytic jet parametrizations for the germs of real analytic CR automorphisms of some essentially finite CR manifolds on their finite jet at a point. As an application we show that the stability groups of such CR manifolds have Lie group structure under composition with the topology induced by uniform convergence on compacta.

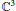
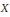
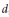
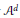
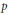
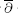Applying the L2 method of solving the -equation, it is shown that compact Kähler manifolds of dimension ≥ 3 admit no Levi flat real analytic hypersurfaces whose complements are Stein.

We propose a procedure to construct new smooth CR-manifolds whose local stability groups, equipped with their natural topologies, are subgroups of certain (finite-dimensional) Lie groups but not Lie groups themselves.

It is shown that any compact Levi flat manifold admitting a positive line bundle is embeddable into ℙn by a CR mapping with an arbitrarily high, though finite, order of regularity.

A real hypersurface M in a complex manifold X is said to be Levi flat if it separates X locally into two Stein pieces. It is proved that there exist no real analytic Levi flat hypersurfaces in ℙ2.