No CrossRef data available.
Article contents
A Real-analytic Nonpolynomially Convex Isotropic Torus with no Attached Discs
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We showbymeans of an example in 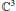 ${{\mathbb{C}}^{3}}$ that Gromov’s theoremon the presence of attached holomorphic discs for compact Lagrangianmanifolds is not true in the subcritical real-analytic case, even in the absence of an obvious obstruction, i.e., polynomial convexity.
${{\mathbb{C}}^{3}}$ that Gromov’s theoremon the presence of attached holomorphic discs for compact Lagrangianmanifolds is not true in the subcritical real-analytic case, even in the absence of an obvious obstruction, i.e., polynomial convexity.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
[1]
Alexander, H., Disks with boundaries in totally real and Lagrangian manifolds.
Duke Math. J.
100(1999), no. 1, 131–138.http://dx.doi.org/10.1215/S0012-7094-99-10004-4
Google Scholar
[2]
Duval, J., Convexite rationnelle des surfaces lagrangiennes.
Invent. Math.
104(1991), no. 3, 581–599.http://dx.doi.Org/10.1007/BF01245091
Google Scholar
[3]
Duval, J. and Gayet, D., Riemann surfaces and totally real tori.
Comment. Math. Helv.
89(2014), 299–312. http://dx.doi.org/10.4171/CMH/320
Google Scholar
[4]
Duval, J. and Sibony, N., Polynomial convexity, rational convexity, and currents.
Duke Math. J.
79(1995), no. 2, 487–513.http://dx.doi.org/10.1215/S0012-7094-95-07912-5
Google Scholar
[5]
Gromov, M., Pseudo-holomorphic curves in symplectic manifolds.
Invent. Math. 82(1985), no. 2, 307–347.http://dx.doi.Org/10.1007/BF01388806
Google Scholar
[6]
Izzo, A. J., H. Kalm, S., and Wold, E. F., Presence or absence ofanalytic strueture in maximal ideal Spaces.
Math. Ann.
366(2016), no. 1-2, 459–478.http://dx.doi.org/10.1007/s00208-01 5-1330-9
Google Scholar
[7]
Jimbo, T., Polynomial hulls ofgraphs on the torus in  . Sci. Math. Jpn.
62(2005), 335–342.Google Scholar
. Sci. Math. Jpn.
62(2005), 335–342.Google Scholar
[8]
Rudin, W., Pairs of inner funetions onfinite Riemann surfaces.
Trans. Amer. Math. Soc.
140(1969), 423–434.http://dx.doi.org/10.1090/S0002-9947-1969-0241629-0
Google Scholar

