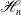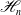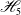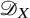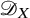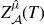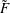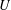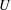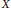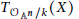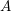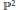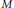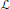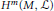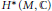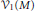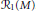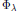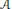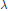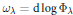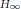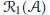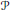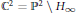Refine search
Actions for selected content:
22 results
Hodge theory of abelian covers of algebraic varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e159
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperpolygonal arrangements
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bernstein–Sato polynomials of locally quasi-homogeneous divisors in
 $\mathbb{C}^{3}$
$\mathbb{C}^{3}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 859-915
- Print publication:
- April 2025
-
- Article
- Export citation
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
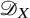 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nearly free curves and arrangements: a vector bundle point of view
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 51-74
- Print publication:
- January 2021
-
- Article
- Export citation
LOCAL NEGATIVITY OF SURFACES WITH NON-NEGATIVE KODAIRA DIMENSION AND TRANSVERSAL CONFIGURATIONS OF CURVES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 January 2019, pp. 123-135
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On Algebraic Surfaces Associated with Line Arrangements
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 471-499
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
A Module-theoretic Characterization of Algebraic Hypersurfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-173
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
POTENTIALS OF A FROBENIUS-LIKE STRUCTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 681-693
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
ON THE MILNOR MONODROMY OF THE IRREDUCIBLE COMPLEX REFLECTION ARRANGEMENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1215-1231
- Print publication:
- November 2019
-
- Article
- Export citation
ON VANISHING THEOREMS FOR LOCAL SYSTEMS ASSOCIATED TO LAURENT POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 18 July 2017, pp. 1-22
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
On Hodge Theory of Singular Plane Curves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-460
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
The Poincaré–Deligne Polynomial of Milnor Fibers of Triple Point Line Arrangements is Combinatorially Determined
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 279-286
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
On the Monodromy of Milnor Fibers of Hyperplane Arrangements
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 697-707
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Admissibility of Local Systems for some Classes of Line Arrangements
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-672
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Tate properties, polynomial-count varieties, and monodromy of hyperplane arrangements
-
- Journal:
- Nagoya Mathematical Journal / Volume 206 / June 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 75-97
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Critical Points and Resonance of Hyperplane Arrangements
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1057
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
Characteristic Varieties for a Class of Line Arrangements
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 56-67
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation