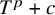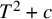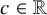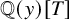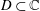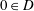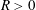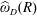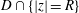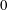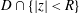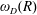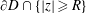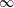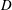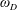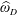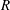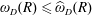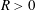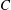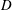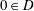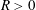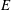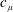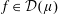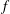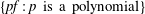Refine search
Actions for selected content:
14 results
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HARMONIC-MEASURE DISTRIBUTION FUNCTIONS AND RELATED FUNCTIONS FOR SIMPLY CONNECTED AND MULTIPLY CONNECTED TWO-DIMENSIONAL REGIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 163-164
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Continuity of condenser capacity under holomorphic motions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 340-348
- Print publication:
- June 2021
-
- Article
- Export citation
On a Property of Harmonic Measure on Simply Connected Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 297-317
- Print publication:
- April 2021
-
- Article
- Export citation
Equality case for an elliptic area condenser inequality and a related Schwarz type lemma
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 91-104
-
- Article
- Export citation
Cyclicity in Dirichlet Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 247-257
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A Convexity Property of Discrete Random Walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 31 March 2016, pp. 928-940
-
- Article
- Export citation
Universality Under Szegő’s Condition
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 211-224
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
The Dependence of Capacities on moving Branch points
-
- Journal:
- Nagoya Mathematical Journal / Volume 186 / 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-27
- Print publication:
- 2007
-
- Article
-
- You have access
- Export citation
BOUNDARY INTERPOLATION SETS FOR CONFORMAL MAPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 4 / August 2006
- Published online by Cambridge University Press:
- 24 July 2006, pp. 607-616
- Print publication:
- August 2006
-
- Article
- Export citation
on littlewood's constants
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 5 / October 2005
- Published online by Cambridge University Press:
- 23 September 2005, pp. 719-726
- Print publication:
- October 2005
-
- Article
- Export citation
Bergman completeness of unbounded hartogs Domains
-
- Journal:
- Nagoya Mathematical Journal / Volume 180 / 2005
- Published online by Cambridge University Press:
- 11 January 2016, pp. 121-133
- Print publication:
- 2005
-
- Article
-
- You have access
- Export citation
TWO-POINT PROJECTION ESTIMATES FOR HARMONIC MEASURE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 4 / July 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 473-478
- Print publication:
- July 2003
-
- Article
- Export citation
ON THERMODYNAMICS OF RATIONAL MAPS. II: NON-RECURRENT MAPS
-
- Journal:
- Journal of the London Mathematical Society / Volume 67 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 24 March 2003, pp. 417-432
- Print publication:
- April 2003
-
- Article
- Export citation