Refine search
Actions for selected content:
21 results
Reversibility and transitivity of semigroup actions on homogeneous spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-20
-
- Article
- Export citation
On Riemannian and Ricci curvatures of homogeneous Finsler manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 73-90
- Print publication:
- March 2025
-
- Article
- Export citation
On denseness of horospheres in higher rank homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 February 2024, pp. 3272-3289
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
- Export citation
Pointwise convergence in nilmanifolds along smooth functions of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1963-2008
- Print publication:
- July 2024
-
- Article
- Export citation
Expanding measures: Random walks and rigidity on homogeneous spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 July 2023, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the spectral theory of groups of automorphisms of S-adic nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 705-726
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TEMPERED HOMOGENEOUS SPACES IV
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 2879-2906
- Print publication:
- November 2023
-
- Article
- Export citation
Arithmeticity of hyperbolic
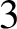 $3$-manifolds containing infinitely many totally geodesic surfaces
$3$-manifolds containing infinitely many totally geodesic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1188-1219
- Print publication:
- March 2022
-
- Article
- Export citation
A BIJECTION OF INVARIANT MEANS ON AN AMENABLE GROUP WITH THOSE ON A LATTICE SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 302-307
- Print publication:
- October 2021
-
- Article
- Export citation
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
Limits of geodesic push-forwards of horocycle invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2782-2804
- Print publication:
- September 2021
-
- Article
- Export citation
Spread out random walks on homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3439-3473
- Print publication:
- November 2021
-
- Article
- Export citation
PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1371-1408
- Print publication:
- July 2021
-
- Article
- Export citation
Limiting distributions of translates of divergent diagonal orbits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1747-1793
- Print publication:
- September 2019
-
- Article
- Export citation
POINT DISTRIBUTIONS IN TWO-POINT HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 26 March 2019, pp. 557-587
- Print publication:
- 2019
-
- Article
- Export citation
Vanishing at infinity on homogeneous spaces of reductive type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1385-1397
- Print publication:
- July 2016
-
- Article
- Export citation
Reduction of Homogeneous Riemannian Structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 18 July 2014, pp. 81-106
-
- Article
-
- You have access
- Export citation
SYMPLECTIC INDUCTION AND SEMISIMPLE ORBITS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 01 June 2005, pp. 446-458
- Print publication:
- June 2005
-
- Article
- Export citation
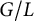
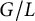
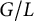
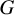
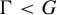
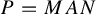
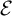
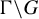
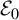
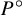
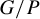
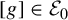
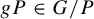
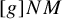
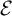
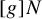
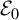
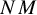
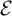
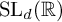
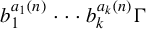


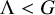
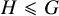
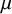
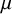
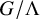
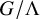
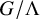


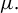
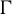
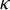
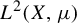
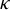
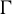
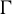
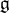
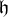
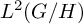
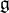
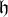
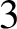

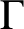
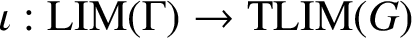
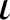
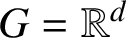
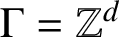
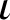
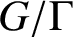

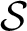
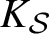
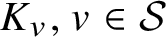
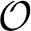
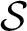
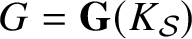
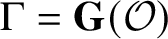
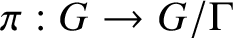
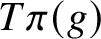
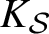
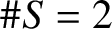
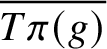

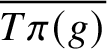
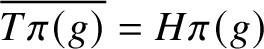
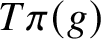
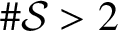
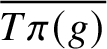
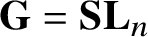
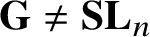
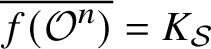
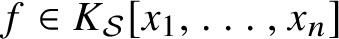
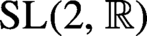
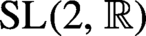
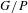
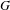
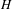
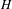
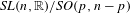
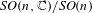


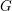
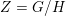
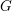
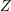
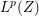
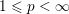
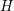
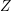
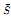 . The situation when
. The situation when 