Refine search
Actions for selected content:
13 results
CHARACTERISATION OF DISTAL ACTIONS OF AUTOMORPHISMS ON THE SPACE OF ONE-PARAMETER SUBGROUPS OF LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 152-175
- Print publication:
- October 2025
-
- Article
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS ADMITTING COMPATIBLE TWO-SIDED INVARIANT METRICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-38
-
- Article
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
- Print publication:
- September 2022
-
- Article
- Export citation
Escaping a Neighborhood Along a Prescribed Sequence in Lie Groups and Banach Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 484-505
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Admissible Sequences for Twisted Involutions in Weyl Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 663-675
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
Cohomology of groups in o-minimal structures: acyclicity of the infinitesimal subgroup
-
- Journal:
- The Journal of Symbolic Logic / Volume 74 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 12 March 2014, pp. 891-900
- Print publication:
- September 2009
-
- Article
- Export citation
A Property of Lie Group Orbits
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 1 / 01 March 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 47-50
- Print publication:
- 01 March 2000
-
- Article
-
- You have access
- Export citation
Exponentiality of Certain Real Solvable Lie Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 368-373
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation
Representations of Lie Groups by Contact Transformations, II: Non-Compact Simple Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 4 / 01 August 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 778-802
- Print publication:
- 01 August 1993
-
- Article
-
- You have access
- Export citation
An Application of Homogenization Theory to Harmonic Analysis: Harnack Inequalities And Riesz Transforms on Lie Groups of Polynomial Growth
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 4 / 01 August 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-727
- Print publication:
- 01 August 1992
-
- Article
-
- You have access
- Export citation
Representations of Lie Groups By Contact Transformations, I: Compact Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 4 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 369-375
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation
On a Relationship Between Adjoint Orbits and Conjugacy Classes of a Lie Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 3 / 01 September 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-304
- Print publication:
- 01 September 1990
-
- Article
-
- You have access
- Export citation
Groups Preserving a Class of Bilinear Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 3 / 01 September 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-271
- Print publication:
- 01 September 1985
-
- Article
-
- You have access
- Export citation
























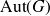
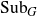
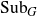
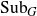
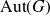
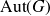
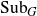
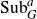
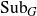
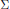


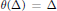
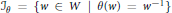
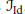
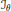
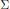


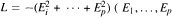 are left invariant Hörmander vector fields) on a connected Lie group
are left invariant Hörmander vector fields) on a connected Lie group 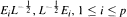 , are bounded on
, are bounded on 